Доказательство этой зависимости проведём на основе гидромеханических представлений

.

Физический смысл (по Эйлеру) – это производная температуры по времени в какой-либо фиксированной точке пространства x = const. В координатах Лагранжа . Физический смысл (по Лагранжу) - производная по времени температуры какой-то частицы, где бы она ни находилась.

Рис.3.4. Векторные линии или линии тока

Линия тока и траектория. Линией тока в поле скорости сплошной среды (в фиксированный момент времени) называется такая кривая, в каждой точке которой вектор скорости направлен по касательной к ней. Линия тока является эйлеровой характеристикой потока; её не следует отождествлять с траекторией - геометрическим местом последовательных положений материальной точки (элементарной жидкой частицы) при её движении в пространстве, которая является лагранжевой характеристикой потока. Траектория - это путь индивидуальной частицы. Поэтому эти линии совпадают только при установившемся движении, когда поле скорости не меняется во времени, т.е. u = u (r). Если же движение неустановившееся, u = u(r,t), то эти линии не совпадают.

Важной особенностью совокупности линий тока в фиксированный момент времени является то, что они никогда не пересекаются друг с другом, за исключением особых точек (например, в случае источника - фонтана). Это следует из того, что скорость в данной точке не может быть касательной одновременно к двум пересекающимся кривым.

Рис. 3.5. Траектория движения частицы

Если элементарный вектор, касательный к линии тока, обозначить через 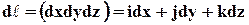, то вследствие того, что вектор коллинеарен , дифференциальные уравнения линий тока можно записать в виде

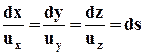. (3.2.7)

Таким образом,

,

,

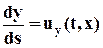(при t = const).

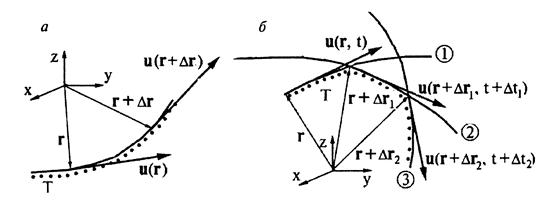Рис.3.6. Линии тока и траектории: а - при установившемся движении совпадают; б - при неустановившемся движении 1,2.3 - линии тока в моменты времени t, t + Dt₁, t + Dt₂. Т - траектории элементарного жидкого объёма показаны пунктиром

Особенности лагранжева и эйлерова методов описания движения сплошной среды продемонстрируем на примере установившегося движения жидкости (рис.3.6), при котором траектория и линия тока совпадают.

При лагранжевом методе (рис.3.4,а) жидкая частица, имеющая при t = t₀ начальную координату r₀ = (x₀, y₀, z₀), движется по траектории, занимая в моменты времени t₀, t₀ +Dt, t₀ + 2Dt, t₀ + 3Dt положения в пространстве, отмеченные на рисунке точками, то есть в параметрическом виде будем иметь .

Скорость этой частицы изменяется со временем; картина течения представляется набором траекторий различных частиц жидкости. При эйлеровом подходе тот же поток (рис.3.6,б) описывается полем скорости u = u(r,t); при установившемся движении, когда 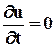, скорость жидкости в любой точке потока зависит только от пространственных координат этой точки 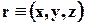. Картина течения характеризуется достаточным набором линий тока.

Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую её точку провести линию тока, то образуется поверхность тока. Если кривая С замкнута, поверхность тока превращается в трубку тока.

Аналитически семейство линий тока в проекциях выглядит следующим образом:

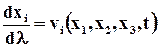(i = 1,2,3). (3.2.8)

Где dl - скалярный параметр. Выражение (3.2.8) – это дифференциальные уравнения линий тока.

Они отличаются от уравнений, описывающих закон движения или траектории движения частиц сплошной среды:

(i = 1,2,3), (3.2.9)

тем, что в уравнениях (3.2.8) t – параметр, а в (3.2.9) t - переменная величина.

Итак, линии тока не совпадают с траекториями. Совпадать они могут только в двух случаях:

1. При установившихся движениях (тогда между двумя последними уравнениями нет различия).

2. При неустановившихся течениях (когда поле скоростей меняется по величине, но не меняется по направлению).

Если какая-либо скалярная величина задана как функция переменных Эйлера, то в каждый момент времени можно рассматривать

поверхность, где

f (x₁, x₂ , x₃ ,t) = const. (3.2.10)

Эта поверхность называется поверхностью равного уровня или эквипотенциальной поверхностью. Вектор, направленный по нормали вкакой-либо точке М эквипотенциальной поверхности (3.2.10) в сторону роста r и равный по величине 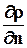, называется вектором-градиентом скалярной функции r в точке М.

Вектор-градиент обозначается как grad r и вычисляется по формуле:

,

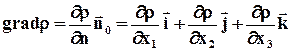где - единичные векторы по направлению и вдоль координатных осей.

Проекция вектора grad r на некоторое направление 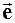определяет изменение плотностей в этом направлении:

где q - угол между направлениями и 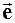; Cos a_I – направляющие косинусы вектора .

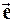Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (3.2.10).

3.3. ПОТОК ГИДРОМЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКИ ЧЕРЕЗ ПОВЕРХНОСТЬ

Законы механики формулируются для выделенных механических систем, или совокупностей физических тел. Для сплошной среды это жидкий объём, т.е. выделенный движущийся объём жидкости (текучего тела), сохраняющий при своём движении все составляющие его части (жидкие частицы). Это понятие соответствует лагранжеву методу описания движения текучих тел.

Эйлеров метод позволяет использовать для решения задач гидромеханики выделенную часть пространства, обычно неподвижную (не связанную с движением среды), которую называют контрольным объёмом. Контрольный объём ограничивается контрольной же поверхностью, сквозь которую течёт сплошная среда. Использование контрольной поверхности и контрольного объёма приводит к использованию понятия потока гидромеханической характеристики (массы, кинетической энергии), т.е. количества этой характеристики, проносимой жидкостью в единицу времени сквозь фиксированную поверхность.

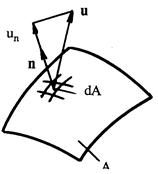Рис.3.7. Поток скорости сквозь контрольную поверхность

Зафиксируем в пространстве, занятом движущейся жидкостью, поверхность А и выделим на этой поверхности около точки с координатами 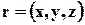элементарную площадку dA(рис.3.7). Скорость жидкости в этой точке равна n - единичный вектор нормали к поверхности в этой же точке. Нормальная к поверхности составляющая скорости будет при этом равной 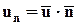. Объём жидкости, протекающей в единицу времени через площадку dA, равен .

В элементарном объёме dQ содержится dQ_B гидромеханической характеристики В, которая проносится жидкостью за единицу времени через площадку dA:

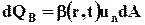(3.3.1)

Поток Q_B гидромеханической характеристики В через контрольную поверхность А (количество характеристики, проносимое жидкостью за единицу времени через поверхность А) составляет

(3.3.2)

Поток гидромеханической характеристики В через контрольную поверхность единичной площади (подынтегральное выражение b ) называется плотностью потока гидромеханической характеристики.

Если принять 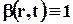, то из (3.3.1) следует, что при этом гидромеханической характеристикой является объём жидкости. Объём жидкости, протекающий через контрольную поверхность за единицу времени, или поток объёма жидкости называется расходом (объёмным расходом) Q:

. (3.3.3)

Если принять , то гидромеханической характеристикой в этом случае будет сама масса жидкости. Поток массы жидкости (масса жидкости, протекающая за единицу времени) через контрольную поверхность А называется массовым расходом Q_м:

. (3.3.4)

Если положить , то получим поток Q_k кинетической энергии через контрольную поверхность:

. (3.3.5)

Положив 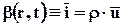, получим поток количества движения Q_I:

. (3.3.6)

В интегралах (3.3.3.)-(3.3.6) выражения представляют собой плотности потоков объёма, массы, кинетической энергии, количества движения, соответственно. Если в поле скорости u (или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой точке её задать нормаль , то для определения объёма жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл:

.

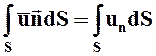Поток скорости сквозь замкнутую поверхность S, отнесённый к единице объёма V, заключённого внутри S, называется расхождением или дивергенцией скорости, т.е.

.

В декартовой системе координат дивергенция скорости вычисляется по формуле:

.

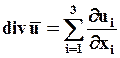Отсюда видно, что дивергенция скорости определяет скорость объёмного расширения жидкости в бесконечно малой окрестности данной точки. Поэтому поток скорости через замкнутую поверхность s должен быть равен расширению всего объёмаvжидкости внутри s, то есть

(3.3.7)

Это равенство называется формулой Гаусса.

3.4. ГИДРОМЕХАНИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ТЕОРЕМЫ ОСТРОГРАДСКОГО - ГАУССА

Зафиксируем неподвижную в пространстве контрольную поверхность А, ограничивающую контрольный объём V. Сквозь эту поверхность протекает жидкость со скоростью 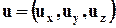. Выделим на ней элементарную площадку dА. Единичный вектор нормали к площадке . Если воспользоваться ортами i, j, k, то

.

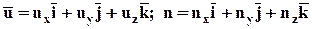Обозначим модуль скорости 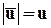; по определению 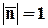. Скалярное произведение двух векторов можно выразить через их проекции:

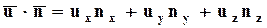, (3.4.1)

а также через модули векторов и угол между ними,

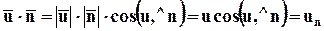(3.4.2)

где u_n - нормальная к поверхности dА составляющая скорости.

Таким образом,

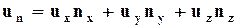. (3.4.3)

Используя (3.4.3), запишем объёмный расход жидкости Q через поверхность dА:

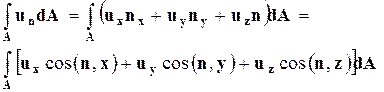. (3.4.4)

Согласно теореме Остроградского - Гаусса имеем

. (3.4.5)

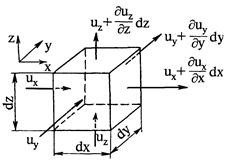Рис. 3.8. Определение расхода жидкости сквозь поверхность элементарного параллелепипеда

Зафиксируем в пространстве параллелепипед с бесконечно малыми рёбрами dx, dy, dz, поверхностью D_iА и объёмом D_iV = dxdydz.

На каждой грани параллелепипеда значение u_n вследствие её малости постоянно и равно проекции скорости на координатную ось, к которой эта грань нормальна.

Пусть проекции скорости имеют направления, указанные на рисунке. Расход жидкости , протекающий сквозь поверхность D_iА, определим как разность между объёмом жидкости, вытекающей из параллелепипеда в единицу времени:

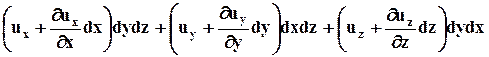
и объём жидкости, втекающей в него за то же самое время:

.

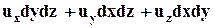В результате имеем

или

, (3.4.6)

где div u - дивергенция вектора скорости, которая определяет собой скалярную величину, определяемую равенством

. (3.4.7)

Если жидкость несжимаемая, то из закона сохранения массы следует, что объём жидкости, втекающей в элементарный объём D_iV равен объёму жидкости, вытекающей из него, так что

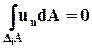. (3.4.8)

Поскольку объём не может быть равным 0, из уравнения (3.4. 6) следует, что в случае несжимаемой жидкости

div u = 0. (3.4.9)

Уравнение (3.4.9) называют уравнением несжимаемости жидкости. Оно справедливо в случае неустановившегося движения жидкости, когда 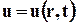для каждого момента времени и в каждой точке потока.

Чтобы обобщить равенство (3.4.6) для произвольного объёма V, ограниченного произвольной поверхностью А (рис.3.9.) разобьём V на элементарные параллелепипеды. Для каждого из них можно записать равенство (3.4. 6).

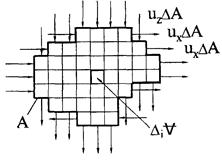Рис.3.9. Определение расхода сквозь произвольную контрольную поверхность

Складывая все эти равенства, можно заметить, что в левой части каждый из интегралов по поверхности D_iА состоит из шести слагаемых по числу граней параллелепипедов. При этом все слагаемые, которые относятся к поверхностям, разделяющим параллелепипеды, взаимно уничтожаются, так как каждая такая поверхность входит в поверхностные интегралы для двух соседних параллелепипедов, и тот объём жидкости, который вытекает из одного параллелепипеда, втекает в другой. Останутся только те части от интегралов , которые относятся к тем граням элементарных параллелепипедов, которые совпадают с контрольной поверхностью А. Следовательно, в левой части сумма интегралов, относящихся ко всем параллелепипедам, будет равна

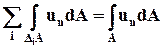. (3.4.10)

В правой части суммы всех уравнений (3.4. 6) по определению интеграла как предела суммы бесконечно малых слагаемых имеем

(3.4.11)

Таким образом, для объёма V произвольной формы справедливо равенство

(3.4.12)

Представив , получим

,

что и составляет содержание теоремы Гаусса - Остроградского.

3.5. ЦИРКУЛЯЦИЯ СКОРОСТИ. ВИХРЬ ВЕКТОРА СКОРОСТИ

Если в поле мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S, то линейный интеграл

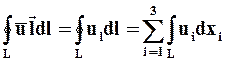
называется циркуляцией скорости, а вектор, определяемый в виде

,

называется вихрем или ротором скорости.

В данном случае - единичные векторы, направленные соответственно по касательной к L и по нормали к поверхности S.

В декартовой системе координат вихрь скорости вычисляется по формуле

.

На основании теоремы Стокса имеет место равенство

.

Проводя аналогию с механикой твердого недеформируемого можно отметить, что при движении элементарного объема жидкости можно выделить два вида движения, которые уже изучались в курсе теоретической механики - поступательное движение твердого тела со скоростью полюса и вращение его вокруг полюса. Для жидкости дополнительным видом движения является деформационное. Поэтому иногда подразделяют движение элементарного объема жидкости на квазитвёрдое (поступательное и вращательное) и деформационное.

Из шести составляющих тензора, описывающего вращение жидкого объема вокруг полюса, только три отличаются друг от друга абсолютной величиной. Каждая из них определяет значение мгновенной угловой скорости вращения вокруг оси, параллельной одной из координатных осей. Эти угловые скорости w_x,w_y,w_z можно рассматривать как проекции на соответствующие координатные оси вектора w, определяющего угловую скорость вращения элементарного объема жидкости при его перемещении в трехмерном пространстве. Например, как было показано выше,

.

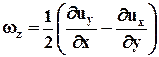Обратим внимание на то, что буква z не входит в качестве индекса или координаты в правую часть равенства, определяющего w_z. Аналогично записываются выражения для w_z и w_у. Вектор w в матричной форме имеет вид

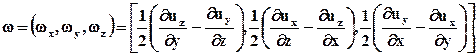. (3.5.1)

В векторном анализе вместо w рассматривают вектор 2w, который обозначают rot u и называют вихрем вектора u (или вихрем скорости):

. (3.5.2)

Рис. 3.10. Сдвиговое продольно-однородное течение (течение Куэтта)

Следует обратить внимание, что ранее рассматривалось лишь пере­мещение объема за бесконечно малые интервалы времени Dt. Если рас­сматривать конечные интервалы времени, то, например, после поворота с угловой скоростью w за время Dt элементарный объем жидкости займет другие точки в поле скорости, и за следующий отрезок времени его угло­вая скорость может измениться. В результате даже при наличии во всех точках скорости 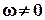и rot u ¹ 0 (такие поля называются вихревыми) мо­жет оказаться, что при перемещении на конечные расстояния эле­ментарного объема жидкости поворот его вокруг полюса не будет вос­приниматься как вращение в обычном смысле. Например, при сдвиговом продольно-однородном течении (течении Куэтта), представленном на рис. 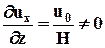3.10 с полем скорости , имеем, что только , а все остальные составляющие тензора grad u равны нулю.

Отметим, что, хотя мгновенная угловая скорость этого объема отлична от нуля,

,

при перемещении объема abсd на большое расстояние его поворот вокруг точки а не воспринимается как вращение.

В том случае, когда все проекции скорости могут быть определены одной функцией j (х₁, х₂, х₃, t) в виде 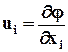, то есть = grad j, то говорят, что поле скоростей потенциальное, а функция j - потенциал скорости.

Проекция скорости v_l на любое направление l определяется производной dj/d l.

Необходимым и достаточным условием существования потенциальных течений являются равенства ():

.

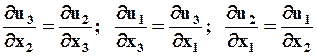Следовательно, безвихревое течение жидкости потенциально.

3.6. ПОЛЯ В ГИДРОДИНАМИКЕ

При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики.

В общем случае поле является пространственным (трёхмерным), иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат.

Если физические величины не зависят от времени, то поле называют стационарным, в противном случае - нестационарным.

При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов.

Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду.

Скалярным называют поле, которое в каждой точке пространства характеризуют одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры).

Основное свойство скалярной функции а(х₁,х₂,х₃) состоит в том, что её численное значение не меняется при преобразовании координат.

Если перейти от старой х₁,х₂,х₃ к новой х^¢₁,х^¢₂,х^¢₃ системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются:

а (х^¢₁,х^¢₂,х^¢₃) = а (х₁,х₂,х₃).

Векторным называют поле, которое в каждой точке пространства характеризуется величиной и направлением.

Например, поле скоростей жидкости. Вектор 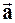в пространстве трёх измерений может быть задан тремя компонентами:

а₁(х₁,х₂,х₃), а₂(х₁,х₂,х₃), а₃(х₁,х₂,х₃),

то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:

а ÜÞ

Введём новую декартову систему координат с тем же началом, но с другим направлением осей.

Пусть l _ij - направляющий косинус оси x^¢_j относительно оси x_i (i = 1,2,3; j = 1,2,3). Вычислим проекции того же вектора на новые оси координат:

a^¢₁ = l ₁₁ a₁ + l ₂₁ a₂ + l_{3 1} a₃;

a^¢₂ = l ₂₁ a₁ + l ₂₂ a₂ + l₂₃ a₃;

a^¢₃ = l ₃₁ a₁ + l ₃₂ a₂ + l₃₃ a₃.

Следовательно, вектор подчиняется определённому закону преобразования его компоненти отличается от скалярной величины, численное значение которой не меняется при преобразовании координат.

То есть,сам вектор не меняется в новых координатах, а меняются его компоненты.

Это выражение можно представить в индексной форме записи как сумму:

Или ещё более короткой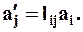

При такой записи пользуются двумя правилами:

1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.

2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3.

Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений.

Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля.

Многие задачи физики и механики сплошной среды приводят к понятию тензора. Тензор, хотя и является обобщением понятия вектора, имеет гораздо более сложный характер. Разница заключается в том, что вектор просто интерпретируется геометрически, у тензора такого наглядного представления не существует.

Описание происходит в прямолинейных (декартовых) системах координат. Координаты обозначаем х₁, х₂, х₃, единичные векторы по осям - i₁,i₂, i₃.

Предположим, что в результате вращения осей координат как единого целого вокруг начала координат, мы перешли к новой системе координат Ox₁´x₂´x₃´. Обозначим косинус угла между осями x_i и x´_k старой и новой системы a_ik = cos (x´_i^x_k). Для удобства пользования дальнейшими формулами приводим таблицу.

Таблица 3.1

	х1	х2	х3
х´1	a11	a12	a13
х´2	a21	a22	a23
х´3	a31	a32	a33

Теперь перейдём к определению тензора. Пусть каждому направлению 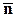соответствует вектор 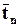(не обязательно коллинеарный n).

Направлениям осей соответствуют векторы 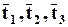, разложение которых опишем подробно:

(3.6.1)

Если векторы 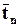для любого направления 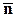выражаются лишь через 3 вектора 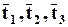согласно формуле

, (3.6.2)

то множество векторов 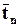образует тензор Т.

Обозначим векторы, определяемые тензором для направлений новых осей . Подставляя в предыдущее выражение (2.6.2) вместо 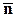направления новых осей (по очереди), получим:

(3.6.3)

Эти условия равносильны (2.6.2) и их можно взять за новое определение тензора, если для каждой системы координат имеется тройка векторов , преобразующаяся по формулам (2.6.3) в тройку 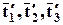, отвечающую другой системе координат, то этим определяется тензор.

Аналогичное определение можно дать и для вектора, если в уравнении (2.6.3) заменить векторы на проекции вектора. Поэтому тензор является обобщением вектора. Формулы (2.6.3) можно записать в сокращённом виде

.

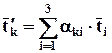Тензор определяется векторами , которые в свою очередь определяются своими компонентами (3.6.1). Поэтому тензор вполне задаётся 9 числами, которые называются компонентами тензора, и обычно записываются в виде

.

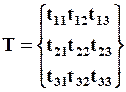Из (2.6.1) и (2.6.3) можно получить формулы преобразования компонент тензора при переходе к новой системе координат:

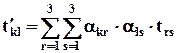, (3.6.4)

где t´_kl – компоненты в новой системе.

Эти формулы можно также взять за определение тензора.

Простейшими примерами являются нулевой и единичный тензоры.

Согласно (2.6.4) у нулевого тензора в любой системе координат компоненты равны 0.

.

Для того, чтобы в дальнейшем не испытывать трудностей при использовании тензоров, запишем некоторые математические правила.

3.6.1.ОПЕРАЦИИ НАД ТЕНЗОРАМИ

1. Умножение тензора на скаляр есть новый тензор, все компоненты которого умножены на этот скаляр (шаровой тензор):

.

2. Сумма тензоров есть новый тензор с компонентами, являющимися суммой одноимённых компонент слагающих тензоров. Так доля Т = Т´ + T´´ должна быть t_ik = t´_ik + t´´_ik. То, что такая сумма есть тензор, следует из линейности формул (4*).

3. Тензор, обладающий свойством t_ik = t_ki, называется симметричным. Если таблицу компонент такого тензора «повернуть» вокруг главной диагонали (то же, что и у определителя), то получится тот же самый тензор.

4. Пусть имеется тензор Т с компонентами t_ik.Составим таблицу с компонентами t_ki (т.е. повёрнутую вокруг главной диагонали). Можно показать, что она также определяет тензор, который называется сопряжённым и обозначается Т*. Очевидно, что (T*)* = T.

5. Тензор, у которого t_ik = - t_ki, называется антисимметричным. Из определения следует, что t_ii = - t_ii, т.е. t_ii = 0 – компоненты главной диагонали равны 0. Антисимметричный тензор всегда можно записать в виде .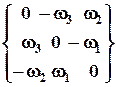

6. Всякий тензор можно разложить на сумму симметричного и антисимметричного тензоров: Т = ½ (Т + Т*) + ½ (Т - Т*). Легко проверить, что в первой скобке стоит симметричный, а во второй – антисимметричный тензор.

7. Пусть дан тензор Т и вектор .Скалярное произведение тензора Т на вектор справа есть новый вектор , обозначаемый (Т, ), компоненты которого равны

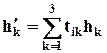(i = 1,2,3).

8. Скалярное произведение тензора Т на вектор слева есть вектор 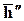, обозначаемый (,Т), компоненты которого равны

.

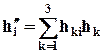9. Из приведённых определений операций ясно, что они должны обладать ассоциативностью и дистрибутивностью, т.е., например,

(Т₁ + Т₂ ) = (Т₁, ) + (Т₂, );

( ₁ + ₂, Т) = ( ₁, Т) + ( ₂, Т);

(l , Т) = (, lТ) = l (, Т).

Но коммутативностью эти операции не обладают, т.е. в общем случае (, Т) ¹ (Т, ). Если Т – симметричный тензор, то равенство выполняется.

10. Пусть даны тензоры А, В с компонентами a_ik и b_ik. Скалярное произведение тензора А на тензор В (А, В)есть новый тензор Т, компоненты которого вычисляются по формулам:

.

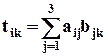Это определение совпадает с определением матричного умножения. Компонент t_ik получается умножением строки с номером i тензора А на столбец с номером j тензора В. Например, t₂₃ = а₂₁b₁₃ + а₂₂ b₂₃ + а₂₃ b₃₃.

11. Скалярное произведение тензоров не обладает свойством коммутативности, т.е. вообще говоря, (А,В) ¹ (В,А).

Перечислим некоторые свойства, которыми оно обладает:

(lА,В) = (А,lВ) = l (А,В); (l - скаляр);

(А₁ + А₂, В) = (А₁,В)+ (А₂,В);

(А,В₁ + В₂) = (А,В₁) + (А,В₂);

[(А,В), С) = (А,(В,С)].

Дата добавления: 2014-12-26