Элементарные деформации. Коэффициент

.

Таким образом, зная три вектора напряжений на взаимно ортогональных площадках и используя уравнения статики, можно найти напряжение на произвольно ориентированной площадке. Следовательно, три вектора напряжений 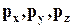полностью характеризуют напряжённое состояние в данной точке пространства.

Представленную в виде квадратной матрицы совокупность девяти проекций на координатные оси трёх векторов, определяющих напряжения в точке сплошной среды, обозначим буквой П:

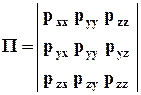. (4.2.9)

Используя матричную форму записи, можно представить равенства (4.2.3), (4.2.4), (4.2.5) в виде

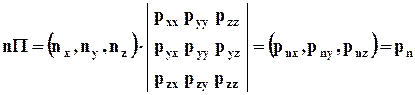. (4.2.10)

Если задать другую систему координатных осей 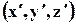, то соответствующие этим осям три вектора напряжений также характеризовали бы напряжённое состояние в этой же точке М.

Матрицы, которые определяют какую-либо физическую величину, т.е. величину, не зависящую от выбора системы координат, называют тензорами. Эти матрицы при введении новой системы координат преобразуются определённым образом.

1. Составляющие матрицы, образующие строки, считаются компонентами векторов, относящихся к площадкам, перпендикулярным соответствующим координатным осям (например, в нашем случае строки 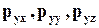являются компонентами вектора напряжения р _у, действующего на площадке, перпендикулярной оси у).

2. Проекции на координатные оси х, у, z векторов, действующих на площадке, перпендикулярные новым координатным осям 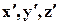, находим, считая, что векторы представляют собой плотности распределения поверхностных сил (напряжений) и что выполняется условие статики, т.е. по уравнениям (4.2.6)-(4.2.8). В общем случае матрица необязательно характеризует напряжённое состояние, поэтому векторы, составляющие строки матрицы, могут быть и не силовыми характеристиками.

3. Определив проекции векторов 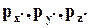на старые координатные оси х, у, z, исходя из геометрических соотношений, находим их проекции на новые координатные оси и из этих проекций образуем матрицу тензора в новой системе координат.

В тензорных обозначениях равенство (4.2.9) можно представить в виде

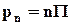(4.2.11)

Как доказывается в тензорном исчислении, сумма диагональных элементов матрицы не зависит от системы координат, в которой она записана. Эта величина называется линейным инвариантом тензора. Для тензора напряжений П имеем

.

Сумма нормальных напряжений по трём взаимно ортогональным площадкам не зависит от ориентации их в пространстве.

Благодаря этому важную роль в механике вязкой жидкости играет гидродинамическое давление р, которое определяется равенством

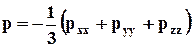(4.2.12)

и может рассматриваться как скалярная величина.

Рассматривая равновесие элементарного (в отношении напряжений) кубика, представленного на рис. 4.2, из равенства нулю суммы моментов поверхностных сил относительно трёх его взаимно ортогональных рёбер (пренебрегая при этом моментом от массовых сил как величиной более высокого порядка малости) получим

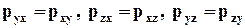. (4.2.13)

Это свойство равенства касательных напряжений свидетельствует о симметричности матрицы тензора напряжений.

В соответствии с определением (4.2.2) единицей напряжения является

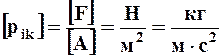ºПа.

На практике часто пользуются производными от паскаля единицами: гектопаскаль (гПа = 100 Па), килопаскалями (кПа = 100 Па) и мегапаскалями (МПа = 1000 000 Па). В этих же единицах измеряется и гидродинамическое давление р.

Дата добавления: 2014-12-26