Метод наименьших квадратов для полиномов

Мы рассматривали функции, зависящие от двух параметров. Предположим, что аппроксимирующая функция имеет вид квадратичной зависимости: .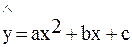

Аналогично линейной зависимости составим функцию

, где 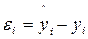( 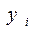-табличное значение, 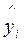- эмпирическая формула).

Возьмем частные производные по a,b и c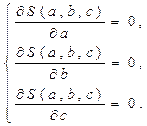

И приравняем их к нулю

Получим нормальную систему уравнений.

-

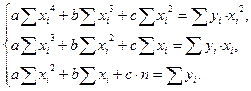Решив нормальную систему относительно неизвестных a,b,с, найдём значения параметров приближающей функции.

Если аппроксимирующая функция является многочленом более высокого порядка “n”, то суть подхода к решению задачи не изменится, а увеличится только число уравнений системы.

Пример 7.2.

Данные предыдущего примера 7.1 аппроксимируем квадратичной зависимостью: 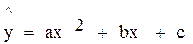. Напомним условие примера

Задание матрицы коэффициентов нормальной системы и столбца ее свободных членов

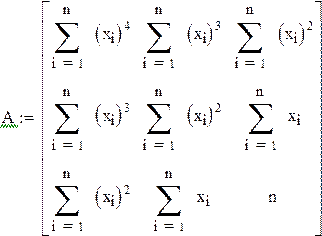
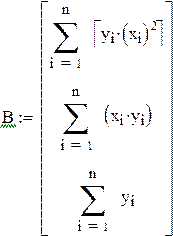
Решение нормальной системы

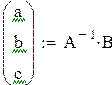
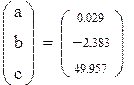
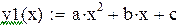
сумма квадратов отклонений

среднеквадратичное отклонение

Рис. 7.3. Решение примера 7.2 в Mathcad

Поскольку величина суммы квадратов отклонений для квадратичной зависимости получилась больше, чем у найденной ранее степенной функции, в данном примере предпочтительнее степенная функция.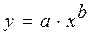

Если аппроксимирующая функция является многочленом более высокого порядка “n”, то суть подхода к решению задачи не изменится, а увеличится только число уравнений системы.

Для построения аппроксимирующей зависимости в виде многочлена в Mathcad можно воспользоваться встроенными функциями regress и interp. Функция regress(x,y,k) возвращает вектор коэффициентов полиномов k-й степени, подобранного методом наименьших квадратов по экспериментальным точкам x и y(x -массив абсцисс, y- массив ординат). Элементы массива x должны быть упорядочены по возрастанию.

Пример 7.3

Продолжим вычисления с данными примера 7.1:

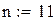
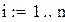
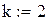
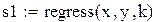
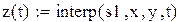
Сумма квадратов отклонений.

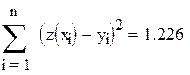
Среднеквадратичное отклонение

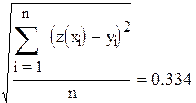
Естественно, результаты такие же, как в примере 7.2

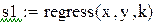
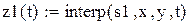
Сумма квадратов отклонений измеренных значений от вычисленных

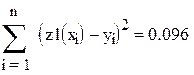
  среднеквадратичное отклонение

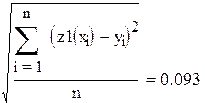
Для кубической параболы получился самый хороший результат

Графики практически совпадают, поэтому не имеет смысла брать приближающий многочлен более высокого порядка.

Рис. 7.4. Решение примера 7.2 в Mathcad

Глава 8. Численное интегрирование

Если функция 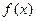непрерывна на отрезке 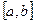и известна ее первообразная 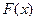, то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница:

,

где 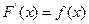. Однако, во многих случаях первообразная функция не может быть найдена с помощью элементарных средств.

Данную функцию 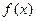на рассмотренном отрезке 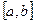заменяют интерполирующей или аппроксимирующей функцией 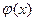простого вида (например, полином), а затем приближенно полагают

.

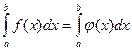Функция 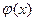должна быть такова, чтобы 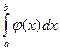вычислялся непосредственно. Если функция 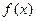задана аналитически, то ставится вопрос об оценке погрешности этой формулы.

Дата добавления: 2014-12-26