Общая формула Симпсона и ее остаточный член

Пусть n=2m есть четное число и - значения функции для равноотстоящих точек с шагом . Применяя формулу Симпсона к каждому удвоенному промежутку длины 2h, будем иметь .

Следовательно, .

Отсюда получаем общую формулу Симпсона:

.

Введя обозначения , формулу можно записать в более простом виде:

.

Если функция непрерывно дифференцируема до четвертого порядка, то ошибка формулы Симпсона на каждом удвоенном промежутке дается формулой:

, где .

Суммируя все эти ошибки, получим остаточный член общей формулы Симпсона в виде:

.

непрерывна на отрезке [ a,b ], поэтому найдется точка такая, что .

Следовательно

, (8.9)

где .

Если задана предельная допустимая погрешность 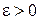, то, обозначив , будем иметь для определения шага h неравенство:

, отсюда 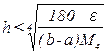, т.е. h имеет порядок . Говорят, что степень точности метода Симпсона равна четырем

Во многих случаях оценка погрешности квадратурной формулы весьма затруднительна. Тогда обычно применяют двойной пересчет с шагами h и 2 h и считают, что совпадающие десятичные знаки принадлежат точному значению интеграла.

Предполагая, что на отрезке [ a,b ] производная 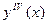меняется медленно, в силу формулы (8.9), получаем приближенное выражение для искомой ошибки

, где коэффициент M будем считать постоянным на промежутке интегрирования. Пусть 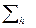и - приближенные значения интеграла , полученные по формуле Симпсона соответственно с шагом h и H=2h. Имеем: и . Отсюда

.

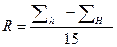За приближенное значение интеграла целесообразно принять исправленное значение

.

Пример 8.2 Вычислить в Mathcad интеграл методом Симпсона для n=8. Оценить остаточный член.

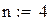
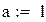
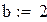
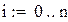
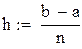
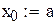
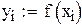
Вычисляем для формулы Симпсона при n=4

Сделаем двойной пересчет при n=8

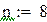
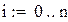
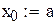
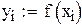
В качестве ответа возьмем

Остаточный член приблизительно равен

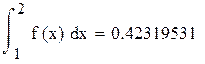
Это точный результат

Рис. 8.3. Решение примера 8.2 в Mathcad

Дата добавления: 2014-12-26