Определение реакций опор. Для рамы, показанной на рис

Пример.

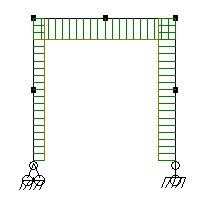
Для рамы, показанной на рис. 2.33, требуется построить эпюры усилий M, Q, N от заданной нагрузки.

Исходные данные: М₁=8 кНм, Р=6 кН, q=4кН/м, h=4 м, l=4 м.

h/2

h/2

l/2

l/2

P

q

M₁

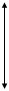
Рис. 2.33

Решение задачи

Для записи уравнений равновесия задаем положительное направление осей координат и момента.

Для определения реакций V_A, V_B и H_A используем уравнения равновесия

S M_B=VA´l+M₁-q´l´l/2-P´h/2=0,

S M_A=M₁+q´l/2´0.75´l-P´h/2-V_B´l=0,

S X=H_A-P=0.

Решая уравнения, получаем V_A=3 kH, V_B=5 kH, H_A=6 kH.

Проверяем полученные результаты с помощью уравнения равновесия

S Y=V_A+V_B-q´l/2=5+3-4´2=0.

Проверка выполняется.

2) Определение числа и границ участков.

Для рассматриваемой рамы имеем 6 участков. Границами участков являются узлы 1, 2, 3, 4, 5, 6, 7.

3) Определение усилий M, Q, N и построение их эпюр.

Рассматриваем участок 1 – 2.

Сечением на участке разделяем раму на две части, верхнюю часть отбрасываем, а нижнюю изображаем отдельно (рис. 2.34а). На схеме показываем реакции опор V_A и V_B, поперечную силу Q и продольную силу N в положительном направлении. Изгибающий момент М в сечении направляем против часовой стрелки (произвольно) и указываем штриховой линией положение растянутого волокна в соответствии с принятым направлением момента (момент направлен от растянутого волокна).

Для рассматриваемой части рамы записываем три уравнения равновестия

S M_O=0, S Y=0, S Z=0,

где о – точка в центре сечения, оси Z и Y показаны на рисунке.

При записи уравнений равновесия используем принятое ранее правило знаков. Имеем три уравнения:

S M_O= -H_A´ z - M=0,

S Y= H_A+Q=0,

S Z=VA+N=0

Решая уравнения, получаем

M= - H_A´ z= -6´ z,

Q= -H_A= -6 kH=const,

N= -V_A= -3 kH=const.

в)

а)

б)

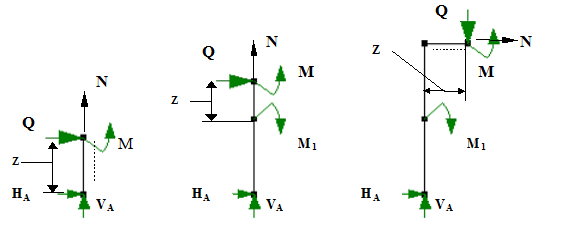
Рис. 2.34

Анализируем полученные результаты для усилий M, Q, N.

а) Усилия Q и N на данном участке постоянные. Следовательно, их эпюры изображаются прямыми линиями, параллельными оси стержня (рис. 2.35 а и б).

б) Изгибающий момент М зависит от координаты z в первой степени. Следовательно, изгибающий момент изменяется по линейному закону, его эпюра на данном участке изображается прямой линией, наклонной к оси стержня (рис. 2.35 в). Для построения эпюры М нужно определить значения момента в начале и в конце участка:

при z=0 M= -6´0=0;

при z=o M= -6´2= -12 кНм.

Так как значение момента получено со знаком миус, то ординату М= -12 кНм откладываем с левой стороны от оси стержня.

Напомним, что на эпюрах Q и N указываются знаки, а эпра М строится на растянутом волокне и знаки на ней не указываются.

+3

52

		+6
		-6
			-6
		- 3
			- 5
		Эпюра N		Эпюра Q
		Рис. 2.35

12

10

16

Эпюра М

Аналогичным образом определены усилия и построены их эпюры на участках 2-3 и 3-4. Расчетные схемы для определения M,Q,N на этих участках показаны на рис. 2.34.б и 2.34.в.

Рассмотрим еще участок 4-5.

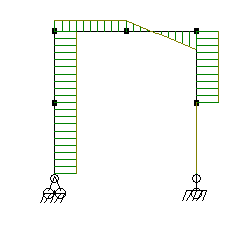
Произвольным сечением на участке разделяем раму на две части, левую отбрасываем и рассматриваем равновесие правой части рамы, показанной на рис. 2.36.а.

Особенность расчета на этом участке по сравнению с участком 1-2 вызвана тем, что на нем действует распределенная нагрузка q. Распределенную нагрузку на участке длиной z заменяем сосредоточенной силой q´z, приложенной посередине этого участка. Затем изображаем усилия Q и N в положительном направлении, изгибающий момнент М направляем по часовой стрелке и показываем штриховой линией положение растянутого волокна в соответствии с принятым направлением момента.

Записываем уравнения равновесия для рассматриваемой части рамы:

S Z= -N-P=0,

S Y=Q -q´z+V_B,

S M_O=M+q´z´z/2+P´2-V_B´z=0.

Решая уравнения, получаем

N= -P= -6 kH=const,

Q=4´ z-5,

M= -2´ z²+5´ z-12.

а) б) в)

Рис. 2.36

Анализируем полученные выражения для усилий M, Q, N.

а) Продольная сила N является постоянной на данном участке, ее эпюра изображается прямой линией, параллельной оси стержня.

б) Поперечная сила Q =4 z -5 изменяется по линейному закону:

при z=0 Q=5 kH,

при z=2 м Q=4´2-5=3 kH.

Эпюра Q изображается прямой линией с ординатами -5 и 3 кН в начале и в конце участка.

в) Изгибающий момент на участке изменяется по нелинейному закону (по квадратичной параболе), его эпюра изображается кривой линией. Для построения эпюры изгибающего момента определяем его значения в начале, в середине и в конце участка:

при z=0 М= -2´0+5´0-12= -12 кНм,

при z=1 м М= -2´1²+5´1-12= -9 кНм,

при z=2 м М= -2´2²+5´2-12= -10 кНм.

Все три значения изгибающего момента получены с отрицательным знаком. Поэтому ординаты М откладываем вверх от оси стержня. Эпюры M, Q, N показаны на рис. 2.35.

На участках 5–6 и 6–7 постройте эпюры самостоятельно. Расчетные схемы для определения M, Q, N на этих участках показаны на рис. 2.36.

Дата добавления: 2014-12-26