Расчет ферм

2.6.1. Общие понятия.

Плоская стержневая система, которая после включений шарниров во все узлы остается геометрически неизменяемой называется фермой.

Примеры ферм показаны на рис.2.37..

В реальных стержневых конструкциях, которые подходят под определение “ферма”, стержни в узлах соединены не шарнирами, а балками, заклепками, сваркой или замоналичены (в железобетонных конструкциях). Тем не менее, в расчетных схемах таких конструкций могут вводится в узлы шарниры, но при условии, что

· стержни являются идеально прямыми;

· оси стержней пересекаются в центре узла;

· сосредоточенные силы приложены только к узлам;

· размеры поперечных сечений стержней значительно меньше их длины.

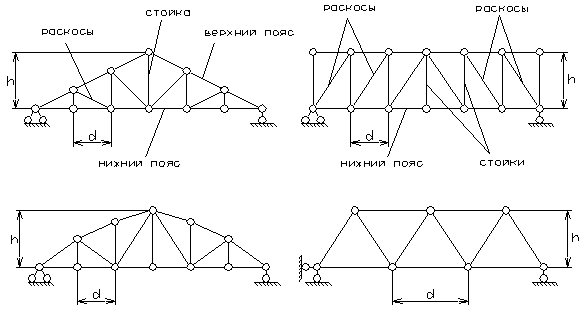
Рис.2.37.. Статически определимые плоские фермы.

При этих условиях стержни фермы работают только на растяжение или сжатие, в них возникают только продольные силы.

Это обстоятельство существенно упрощает расчет стержневой системы и позволяет получать результаты с достаточной степенью точности.

Для определения усилий в стержнях фермы методом сечений необходимо:

1) Сечение проводить таким образом, чтобы оно

· пересекало ось стержня, в котором определяется усилие;

· пересекало по возможности не более трех стержней;

· разделяло ферму на две части.

2) Продольные усилия в стержнях направлять в положительном направлении, т.е. от узла.

3) Выбирать такие уравнения равновесия для части фермы, которые включали бы лишь одно искомое усилие. Такими уравнениями являются, например,

· сумма моментов относительно точки, в которой пересекаются лини действия усилий в стержнях ферм, разрезанных сечением; такие точки принято называть моментными;

· сумма проекций сил на вертикальную ось для раскосов ферм с параллельными поясами.

4) Для определения усилий в стойках вырезать узлы, если в них сходится не более трех стержней.

5) Для упрощения определения плеч внутренних усилий относительно моментной точки при составлении уравнений моментов при необходимости заменять искомые усилия их проекциями на взаимно перпендикулярные оси.

2.6.2. Определение усилий в стержнях фермы.

Для определения усилий в стержнях фермы необходимо:

· определить реакции опор;

· методом сечений определить требуемые усилия;

· произвести проверку полученных результатов.

Реакции опор в простых балочных фермах, показанных на рис.2.37, определяются также как в однопролетных балках с помощью уравнений вида

, .

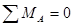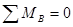Для проверки реакций опор используем уравнение

.

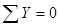Рассмотрим алгоритм расчета на конкретном примере.

Дана расчетная схема фермы (рис.2.38).

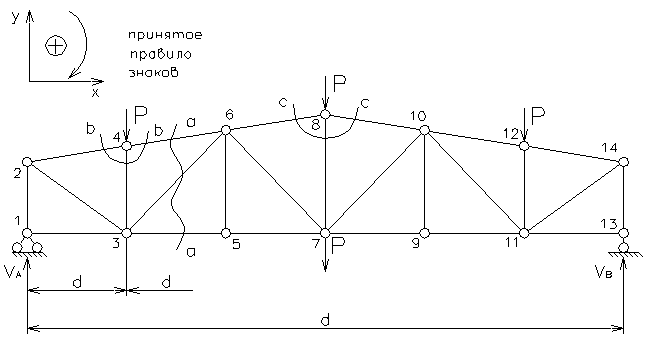
Рис.2.38

Требуется определить усилия в стержнях 4-6, 3-6, 3-5, 3-4, 7-8.

Решение задачи.

1) Определяем реакции опор.

Для этого используем уравнение равновесия:

, .

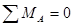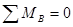Записываем уравнения, используя принятое правило знаков:

Решая уравнения, находим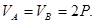

Проверяем реакции опор по уравнению .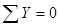

2) Определяем усилия в стержнях фермы.

а) Усилия в стержнях 4-6, 3-6, 3-5.

Для определения усилий в указанных стержнях разрезаем ферму сечением а-а на две части и рассматриваем равновесие левой части фермы (рис.2.39.

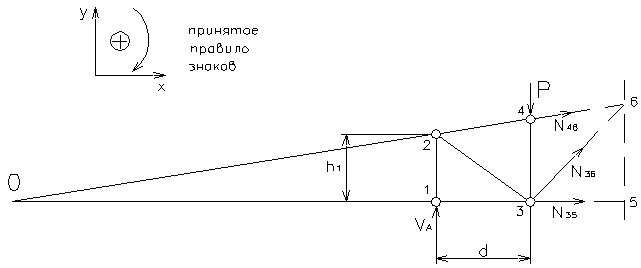
Рис.2.39

К левой части фермы прикладываем реакцию опоры , силу , действующую в узле 4, и искомые усилия в стержнях фермы 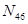, , 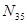. Эти усилия направляем вдоль соответствующих стержней в сторону от узла, то есть в положительном направлении.

Для определения усилий 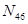, , 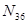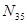можно использовать следующую систему уравнений:

, , .

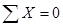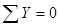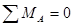Но в этом случае получим совместную систему уравнений, в которые будут входить все искомые усилия.

Для упрощения решения задачи необходимо использовать уравнения равновесия, в которые входило бы только одно неизвестное.

Для определения усилия 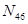таким уравнением является

,

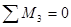т. е. сумма моментов относительно узла 3, в котором пересекаются линии действия усили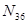й и 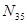, так как моменты этих сил относительно узла 3 равны нулю. Для усилия 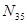таким уравнением является

,

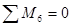т. е. сумма моментов относительно узла 6, в котором пересекаются линии действия усили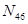й и .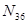

Для определения усилия 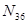следует использовать уравнение суммы моментов относительно точки О, в которой пересекаются линии действия усили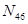й и 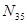, т. е.

.

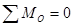При записи указанных уравнений возникают математические трудности по определению плеч сил относительно соответствующих точек. Для упрощения решения этой задачи рекомендуется разложить искомое усилие по осям Х, Y и использовать проекции усилия при записи уравнения равновесия.

Покажем это на примере усилия 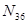(рис.2.40).

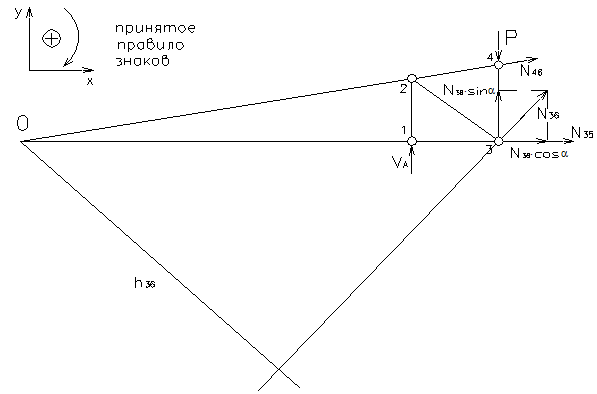
Рис.2.40

Запишем уравнение :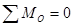

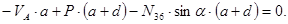
Решая уравнение, получаем:

.

В данном примере проекция усилия 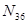на ось Х имеет момент относительно точки О равный нулю, так как линия её действия проходит через точку О.

3) Определяем усилие в стержне 3-4.

Для определения усилия вырезаем в узел 4 фермы сечением b-b (рис.2.41.а).

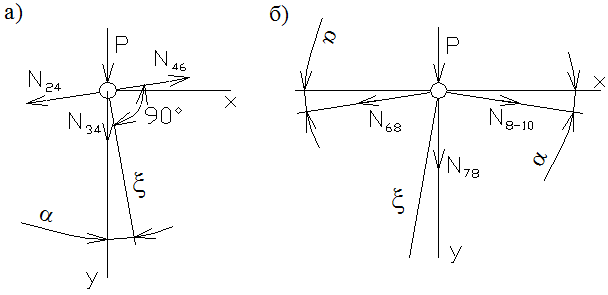
Рис.2.41

Далее выбираем уравнение равновесия, в которое входило бы только усилие . В данном случае – это сумма проекций всех сил, приложенных в узле, на ось x, перпендикулярную к линии действия усилий и :

откуда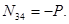

4) Определяем усилие в стержне 7-8.

Вырезаем узел 8 сечение с-с (рис.2.41.б). Составляем два уравнения равновесия

Для определения усилия 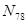имеем два уравнения с тремя неизвестными. Следовательно, одно из этих неизвестных ( 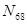или 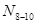) должно быть определено предварительно.

Если усилие известно, то для определения усилия можно использовать уравнение:

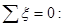
сумма проекций сил, приложенных в узле, на ось x, перпендикулярную линии действия силы .

Необходимо отметить, что усилия в стержнях фермы можно определять, рассматривая поочередно равновесие её узлов и составляя для каждого узла по два уравнения

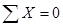и .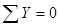

Начинать необходимо с узла, в котором сходятся только два стержня, а затем последовательно рассматривать узлы, в которых только два неизвестных усилия. Рассмотрим пример (рис.2.42).

Рис.2.42

1) Рассматриваем узел 1, в котором сходятся только два стержня. Составляем и решаем уравнения

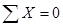и :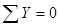

; .

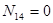2) Рассматриваем узел 2, в котором сходятся 3 стержня, но известно усилие :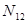

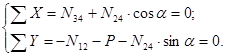
Решая систему уравнений, находим:

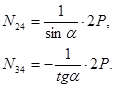
Затем рассматривается узел 4 и т. д.

Такой способ определения усилий в стержнях фермы имеет следующие недостатки:

· ошибка, допущенная в процессе расчета, распространяется на последующие вычисления;

· он не рационален для определения усилий лишь в отдельных стержнях фермы.

К достоинствам способа относится возможность применения при составлении программ для расчета на ЭВМ.

2.6.3. Проверка результатов расчета.

Для проверки результатов расчета нужно использовать уравнения равновесия, которые включают наибольшее число усилий. Так, например, для проверки усилий 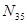, , 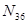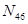(рис.3.3) такими уравнениями являются

, .

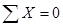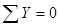Дата добавления: 2014-12-26