
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Головина О.В., 2013 г
|
|
|
|
Калуга– 2013
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
О.В. Головина
Калужский филиал
Алгоритм расчета трехшарнирных арок можно использовать для расчета трехшарнирных рам, опоры которых расположены на одном уровне, а нагрузки вертикальные.
государственного образовательного учреждения
высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
И САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ
Инженерно-технических специальностей
по дисциплине МАТЕМАТИКА (Высшая математика)
| УДК 51(076) К92 | Утверждено учебно-методическим советом Смоленского филиала МИИТ «___»___________20__ г. Протокол № ___ |
Автор:
О.В. Головина, канд. пед. наук, доцент кафедры «Высшая и прикладная математика» РОАТ МИИТ
Рецензенты:
Н.В. Никаноркина, кандидат педагогических наук, доцент кафедры «Высшая математика и статистика» Калужского филиала ГОУ ВПО «Финансовый университе при правительстве РФ»;
Л.В. Степанова, кандидат физико-математических наук наук, доцент кафедры «Высшая и прикладная математика» Смоленского филиала МИИТ.
| Головина О.В. | |
| К92 | Методические рекомендации к практическим занятиям и самостоятельной работе студентов по дисциплине «математика»/ О.В. Головина.- Калуга, 2013 - 84с. |
Методические рекомендации предназначены для студентов 1-го курса инженерно-технических специальностей и содержат материал, изучаемый в 1 семестре. Работа может быть полезна также студентам 1-го курса дневного отделения, специальности 190205 «Подъемно-транспортные, строительные, дорожные машины и оборудование», а также студентам заочного отделения всех технических специальностей.

 © Калужский филиал МИИТ, 2013 г.
© Калужский филиал МИИТ, 2013 г.
Данное методическое пособие предназначено для проведения практических занятий по дисциплине «математика» в течение 1 семестра для студентов 1 курса инженерно-технически
Рабочей программой по математике за 1 семестр предусмотрено изучение следующих разделов: элементы векторной алгебры; аналитическая геометрия элементы линейной алгебры; элементы высшей алгебры; элементы топологии; введение в математический анализ; дифференциальное исчисление функции одной переменной. Теоретический материал каждого из этих разделов излагается преподавателем в лекционном курсе. При этом изучение каждого теоретического вопроса сопровождается разбором практических задач и упражнений.
Целью практических занятий является контроль знаний студентов, полученных на лекциях, и отработка навыков по решению соответствующих задач и упражнений. Помощь в этом как преподавателю, так и студенту, призвано оказать данное пособие, содержащее методические указания ко всем 23 практическим занятиям, предусмотренным учебным планом.
Все практические занятия имеют единую структуру: тема, план занятия, методические рекомендации по проведению занятия, контрольные вопросы, задания, выполняемые на занятии, задания для самостоятельной работы студентов, литература. В пособии содержаться также ответы к большинству предлагаемых заданий.
Студенту при подготовке к каждому практическому занятию необходимо изучить соответствующий лекционный материал, познакомится с планом занятия, и быть готовым ответить на вопросы, приведенные в каждой теме. Вопросы составлены таким образом, чтобы охватить основные и наиболее важные теоретические положения изучаемой темы. Каждый студент должен не только понимать, но и уметь сформулировать, т.е. произнести в слух, все основные понятия, определения и теоремы. Наличие контрольных вопросов направлено на активизацию процесса обучения, на развитие логического мышления, упорства в достижении цели. При необходимости и с целью углубления своих знаний каждый студент может обратиться к дополнительной литературе, список которой указан в данном пособии.
Каждое практическое занятие содержат оптимальное количество заданий для изучения основных вопросов темы. В связи с тем, что решение большинства типовых задач рассматривается на лекциях, данное пособие играет роль задачника с подборкой необходимых упражнений. Многие практические занятия составлены таким образом, чтобы у преподавателя была возможность выбора задания, варьирования трудности выполняемых упражнений.
В связи с довольно большим объемом изучаемого материала некоторые задания из аудиторной работы при нехватке времени могут быть вынесены на самостоятельное изучение.
Задачи, рекомендованные для самостоятельной работы студентов, могут быть использованы в качестве домашнего задания с последующей проверкой их выполнения. Задания для самостоятельной работы студентов в большинстве аналогичны заданиям, выполняемым в аудитории, их целью является закрепление полученных знаний, приемов и методов решения. Дополнительные задания призваны помочь студенту сформировать твердые навыки решения задач, что является необходимым условием дальнейшего успешного обучения.
По окончанию 1 семестра студенты сдают зачет по дисциплине «математика», практическая часть которого предполагает умение решать основные задания из данного пособия. Поэтому последовательность и систематичность в подготовке к практическим занятиям гарантирует успешное освоение материала.
Практическое занятие № 1 (2 часа).
Тема: Матрицы и определители.
План:
1. Матрицы. Основные сведения о матрицах. Операции над матрицами.
2. Определители квадратных матриц 2-го и 3-го порядка.
3. Определитель n-го порядка. Теорема Лапласа.
Методические рекомендации к занятию. Надо хорошо уяснить, что матрица – это прямоугольная таблица чисел, состоящая из m строк и n столбцов. Необходимо знать, как устанавливаются размеры матрицы и её порядок, уметь выполнять транспонирование матриц, алгебраические операции над ними (умножение матрицы на число, сложение, вычитание, умножение матриц).
Относительные трудности возникают при усвоении операции умножения матриц. Необходимо твердо усвоить формальное правило умножения и связанное с ним условие существования произведения АВ матриц А и В: число столбцов матрицы А должно быть равно числу строк матрицы В. Одна из особенностей операции умножения состоит в том, что произведение матриц в общем случае некоммутативно, т.е. 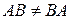 . Если матрицы А и В не квадратные, то это свойство очевидно, так как либо одно из произведение,
. Если матрицы А и В не квадратные, то это свойство очевидно, так как либо одно из произведение, 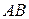 или
или  , не существует, либо
, не существует, либо 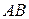 и
и  – матрицы разных размеров. Даже если А и В – квадратные матрицы, то общем случае
– матрицы разных размеров. Даже если А и В – квадратные матрицы, то общем случае 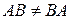 , в чем нетрудно убедиться на любом частном примере.
, в чем нетрудно убедиться на любом частном примере.
Другая особенность произведения матриц или квадрата ненулевой матрицы может оказаться нулевой матрицей.
Следует четко уяснить, что если матрица – это таблица чисел, то определитель квадратной матрицы – это число, характеризующее матрицу и вычисляемое по определенным правилам. Необходимо уметь по этим правилам вычислять определители второго и третьего порядков.
При изучении свойств определителей особое внимание следует обратить на теорему Лапласа. Необходимо уметь пользоваться свойствами определителей при вычислении определителей четвертого и более высоких порядков.
Контрольные вопросы
1. Что называется матрицей?
2. Какие виды матриц вы знаете?
3. Какие операции над матрицами вы знаете?
4. Как производится операция умножения матрицы на число?
5. Как складываются две матрицы одинакового размера?
6. Какое условие должно выполняться при нахождении произведения двух матриц?
7. Чему равен определитель матрицы, состоящей из одного элемента?
8. По какой формуле вычисляется определитель матрицы второго порядка?
9. По какой формуле вычисляется определитель матрицы третьего порядка?
10. Как свойства определителей вы знаете?
11. Как вычисляется определитель матрицы с помощью теорему Лапласа?
12. Когда целесообразно применять теорему Лапласа?
Практические задания, выполняемые на занятии
1.1. Найти сумму матриц А и В.
 и
и  .
.
1.2. Вычислить матрицу 2А+5В, если 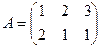 ,
, 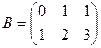 .
.
1.3. Даны матрицы 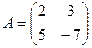 и
и  Найти АВ и ВА.
Найти АВ и ВА.
Замечание. Очевидно, что 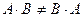 , т.е. произведение матриц не коммутативно.
, т.е. произведение матриц не коммутативно.
1.4. Найти произведение  , если
, если
а) 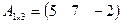 ,
, 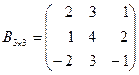 ; б)
; б) 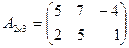 ,
, 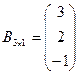 ;
;
в)  ,
,  .
.
1.5. Вычислить матрицу  .
.
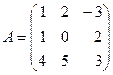 ,
,  ,
, 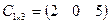 , Е – единичная матрица.
, Е – единичная матрица.
1.6. Вычислить 2-го порядка определитель.
а)  ; б)
; б)  ; в)
; в) 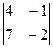 ; г)
; г)  ; д)
; д) 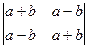 .
.
1.7. Вычислить определитель3-го порядка.
а) 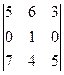 ; б)
; б) 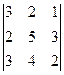 .
.
1.8. Вычислить алгебраические дополнения всех элементов матрицы

1.9. Вычислить определитель3-го порядка, используя теорему Лапласа.
а)  ; б)
; б)  ; г)
; г) 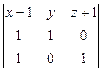 .
.
1.10. Вычислить определитель 4-го порядка.
а) 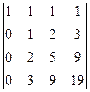 ; б)
; б)  .
.
в) Вычислить определитель, разложив его по элементам 3-ей строки
 .
.
1.11. Вычислить определитель, пользуясь свойствами определителей.
а) 
Указания:
1. из первого столбца вычитаем четвертый;
2. раскладываем по элементам 1-го столбца;
3. из 1-ой строки отнимаем 3 вторых; из 3-ей строки отнимаем 2 вторых строки;
4. раскладываем по элементам 1-го столбца.
б)  .
.
Задания для самостоятельной работы
1.12. Найти произведение матриц:
а)  ; б)
; б)  ; в)
; в)  .
.
1.13. Вычислить определитель, разложив его по элементам 3-го столбца.
а)  ; б)
; б)  ; в)
; в)  .
.
Практическое занятие № 2 (2 часа).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 507; Нарушение авторских прав?; Мы поможем в написании вашей работы!