Тема: Системы линейных уравнений

План.

Тема: Обратная матрица. Ранг матрицы.

1. Определение обратной матрицы. Алгоритм нахождения обратной матрицы.

2. Матричные уравнения.

3. Ранг матрицы.

Методические рекомендации к занятию. Нужно знать определение присоединенной и обратной матриц, уметь их вычислять, знать, что для существования матрицы 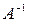обратной матрице 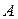, необходимо и достаточно, чтобы матрица 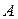была невырожденной (неособенной). Проверить правильность вычисления обратной матрицы можно, составив произведение 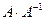или 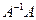. Если оно является единичной матрицей Е, то в соответствии с определением матрица 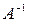вычислена правильно.

Контрольные вопросы

1. Какая матрица называется обратной к данной матрице?

2. Необходимое и достаточное условие существования обратной матрицы?

3. Алгоритм нахождения обратной матрицы.

4. Что называется рангом матрицы?

5. Как мы находим ранг матрицы?

6. Какие элементарные преобразования вы знаете?

7. Какая матрица называется ступенчатой?

8. Чему равен ранг ступенчатой матрицы?

9. Какие виды матричных уравнений можно решить с помощью обратной матрицы?

Практические задания, выполняемые на занятии

2.1. Доказать, что матрица 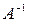является обратной для матрицы .

, .

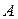2.2. При каких значениях 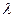матрица 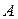не имеет обратной.

.

2.3. Найти матрицу, обратную для матрицы , пользуясь определением обратной матрицы:

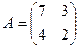а) ; б) .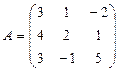

2.4. Найти ранг матрицы

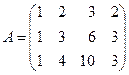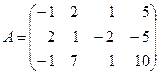а) ; б) ; в) .

2.5. Найти матрицу, обратную для матрицы 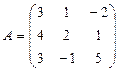, пользуясь методом Жордана-Гаусса.

2.6. Найти матрицу, обратную данной

а) 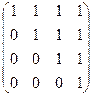; б) ; в) .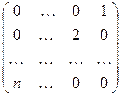

2.7. Решить матричные уравнения.

а) ;

б) ;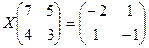

в) ;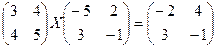

г) .

Задания для самостоятельной работы

2.8. Найти матрицу, обратную для матрицы 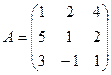, пользуясь определением обратной матрицы и методом Жордана-Гаусса.

2.9. Найти матрицу, обратную данной

а) 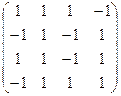; б) ; в) .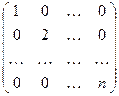

2.10. Решить матричные уравнения.

а) ;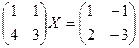

б) ;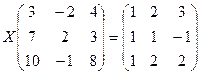

в) ;

г) .

Практическое занятие № 3 (2 часа).

Дата добавления: 2014-12-26