
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно малые и бесконечно большие функции. 6 страница
|
|
|
|
9. Сформулируйте теорему Лагранжа.
10. В чём состоит геометрический смысл теоремы Лагранжа?
11. В чем состоит достаточное условие возрастанию (убывания) функции на интервале?
12. Какие точки называются критическим?
13. Какая точка называется точкой максимума (минимума) функции?
14. что называется максимумом (минимумом) функции?
15. Какие значения называются экстремумами функции?
16. Может ли некоторый максимум функции быть меньше какого-либо минимума функции?
17. Сформулируйте теорему Ферма (необходимое условие существования экстремума).
18. В чем состоит достаточное условие существования экстремума?
19. Какой график называется выпуклым вверх (вниз)?
20. Какие интервалы называются интервалами выпуклости графика функции?
21. Какая точка называется точкой перегиба графика функции?
22. В чём состоит достаточное условие выпуклости графика функции.
23. Какая прямая называется наклонной асимптотой графика функции?
24. По каким формулам находятся коэффициенты 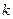 и
и 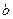 в том случае, когда прямая
в том случае, когда прямая 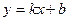 является асимптотой графика функции?
является асимптотой графика функции?
25. Какая прямая называется горизонтальной асимптотой графика функции?
26. Какая прямая называется вертикальной асимптотой графика функции?
27. Какая схема используется при построении графика функции?
Практические задания, выполняемые на занятии
21.1. Найти предел функции, пользуясь правилом Лопиталя:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 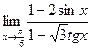 ;
;
5) 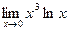 ; 6)
; 6) 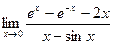 .
.
21.2.* Найти пределы следующих функций (неопределенности вида 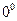 ,
, 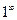 ,
, 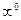 ):
):
1) 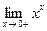 ; 2)
; 2) 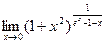 ; 3)
; 3) 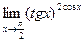 .
.
21.3. Составить уравнения касательной и нормали к данной кривой в заданной точке. Сделать чертеж:
1) 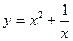 ,
,  ; 3)
; 3)  ,
,  ;
;
2)  ,
, 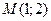 ; 4)
; 4)  ,
, 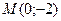 ;
;
5)  ,
,  .
.
21.4. Найти интервалы возрастания и убывания функции
а) 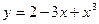 ;
;
б) 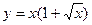 ;
;
в) 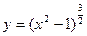 .
.
21.5. Найти экстремумы функции:
1) 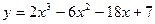 ;
;
2) 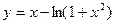 ;
;
3)  ;
;
4)  ;
;
5)  .
.
21.6. Найти наибольшие и наименьшие значения функций на промежутках:
1)  ,
,  ;
;
2) 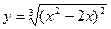 ,
,  ;
;
3) 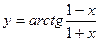 ,
, 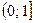 .
.
21.7. Найти асимптоты графиков функций:
1)  ; 2)
; 2) 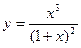 ; 3)
; 3) 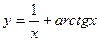 .
.
21.8. Найти точки перегиба и интервалы выпуклости функций:
1) 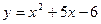 ; 2)
; 2)  ; 3)
; 3)  .
.
21.9. Исследовать функцию и построить её график:
1) 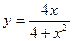 ; 2)
; 2)  ; 3)
; 3) 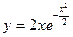 ; 4)
; 4)  ; 5)
; 5) 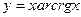 .
.
Задания для самостоятельной работы
21.10. Найти предел функции, пользуясь правилом Лопиталя:
1)  ; 2)
; 2) 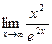 ; 3)
; 3) 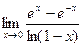 ; 4)
; 4) 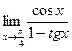 ;
;
5) 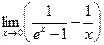 ; 6)
; 6) 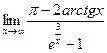 .
.
21.11.* Найти пределы следующих функций (неопределенности вида 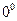 ,
, 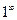 ,
, 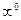 ):
):
1) 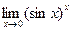 ; 2);
; 2);  ; 3)
; 3)  .
.
21.12. Составить уравнения касательной и нормали к данной кривой в заданной точке. Сделать чертеж:
1) 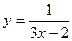 ,
,  ; 3)
; 3)  ,
,  ;
;
2) 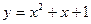 ,
, 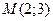 ; 4)
; 4) 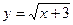 ,
, 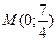 ;
;
5)  ,
, 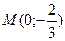 .
.
21.13. Найти интервалы возрастания и убывания функции:
а)  , если
, если  ; б)
; б) 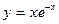 ; в)
; в) 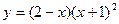 .
.
21.14. Найти экстремумы функции:
1) 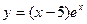 ; 4)
; 4) 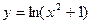 ;
;
2)  ; 5)
; 5) 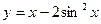 .
.
3)  ;
;
21.15. Найти наибольшие и наименьшие значения функций на промежутках:
1) 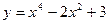 ,
, 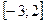 ; 2)
; 2)  ,
, 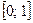 ; 3)
; 3)  ,
, 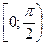 .
.
21.16. Найти асимптоты графиков функций:
1) 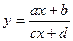 ; 2)
; 2)  ; 3)
; 3)  .
.
21.17. Найти точки перегиба и интервалы выпуклости функций:
1) 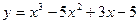 ; 2)
; 2) 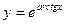 ; 3)
; 3) 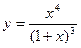 .
.
21.18. Исследовать функцию и построить её график:
1) 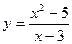 ; 2)
; 2)  ; 3)
; 3) 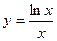 ; 4)
; 4) 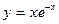 ; 5)
; 5) 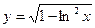 .
.
Практическое занятие № 22 (2 часа).
Тема: Векторная функция скалярного аргумента. Пространственная кривая
План:
1. Определение векторной функции скалярного аргумента.
2. Предел и непрерывность векторной функции скалярного аргумента.
3. Производная и дифференциал векторной функции скалярного аргумента.
Методические рекомендации к занятию. Аналогично схеме изучения функции одной переменой в данной теме необходимо дать понятие векторной функцией скалярного аргумента, определить способы её задания и физическую интерпретацию, ввести понятие предела, непрерывности, производной и дифференциала векторной функции скалярного аргумента. Необходимо знать также определение пространственной кривой и способы её задания, уметь находить уравнение касательной и уравнение нормальной плоскости к пространственной кривой.
Контрольные вопросы
1. Что называется векторной функцией скалярного аргумента?
2. Как задается векторная функция скалярного аргумента?
3. Что является скалярным аргументом векторной функции в механике?
4. Что называется годографом векторной функции скалярного аргумента?
5. Что называется пределом векторной функции скалярного аргумента?
6. Когда векторная функция скалярного аргумента непрерывна в некоторой точке?
7. Что называется производной векторной функции скалярного аргумента?
8. Как вычисляется производная векторной функции скалярного аргумента?
9. В чем состоит физический смысл производной векторной функции скалярного аргумента?
10. В чем состоит геометрический смысл производной векторной функции скалярного аргумента?
11. Что называется дифференциалом векторной функции скалярного аргумента?
12. В чем состоят свойства производной и дифференциала векторной функции скалярного аргумента?
13. Как находится производная скалярного произведения вектор-функций?
14. Как находится производная векторного произведения вектор-функций?
15. Как находится производная смешанного произведения вектор-функций?
16. Как задается пространственная кривая?
17. Как найти уравнение касательной к пространственной кривой  ?
?
18. Как найти уравнение нормальной плоскости к пространственной кривой  ?
?
19. По какой формуле вычисляется дифференциал дуги пространственной кривой  ?
?
Практические задания, выполняемые на занятии
22.1. Найти вектор-функцию  , описывающую равномерное вращение точки против часовой стрелки по окружности радиуса
, описывающую равномерное вращение точки против часовой стрелки по окружности радиуса 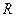 с угловой скоростью
с угловой скоростью 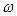 .
.
22.2. Радиус-вектор движущейся точки в любой момент времени задается уравнением 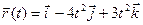 . Найти скорость, ускорение и траекторию движения.
. Найти скорость, ускорение и траекторию движения.
22.3. Какая линия является годографом вектор-функции 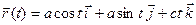 ?
?
22.4. Найти годограф вектор-функции:
а)  ,
,  ;
;
б) 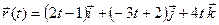 ,
,  .
.
22.5. Найти производную скалярного произведения вектор-функций:  и
и  .
.
22.6.  ,
,  . Найти
. Найти  .
.
22.7. Составить уравнения касательной и нормальной плоскости к кривой  ,
,  ,
, 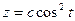 в точке
в точке 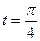 .
.
Задания для самостоятельной работы
22.8. Найти годограф вектор-функции:
а)  ;
;
б)  ;
;
в) 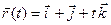 .
.
22.9. Показать, что векторы 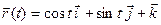 и
и  перпендикулярны.
перпендикулярны.
22.10. Составить уравнения касательной к кривой 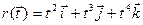 в точке
в точке  .
.
22.11. Составить уравнения касательной и нормальной плоскости к винтовой линии  в точке
в точке 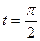 .
.
22.12. Составить уравнение винтовой линии, если радиус основания цилиндра 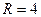 , шаг
, шаг 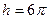 , и найти дифференциал её дуги.
, и найти дифференциал её дуги.
22.13. Найти дифференциал дуги кривой  ,
, 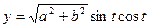 ,
, 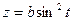
22.14. Уравнение движения имеет вид 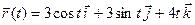 , где
, где  время. Определить скорость и ускорение движения в произвольный момент времени.
время. Определить скорость и ускорение движения в произвольный момент времени.
Практическое занятие № 23 (2 часа).
Тема: Кривизна плоской и пространственной кривой.
План:
1. Понятие кривизны плоской кривой.
2. Центр кривизны, круг кривизны. Эволюта и эвольвента.
3. Кривизна и кручение пространственной кривой.
4. Сопровождающий трехгранник пространственной кривой.
Методические рекомендации к занятию. При изучении данной темы студенты должны уметь находить кривизну плоской и пространственной кривых, находить радиус кривизны, центр кривизны, определять эволюту и эвольвенту. Важно также уметь находить составляющие сопровождающий трехгранник пространственной кривой: соприкасающуюся, нормальную и спрямляющую плоскости.
Контрольные вопросы
1. Что называется углом смежности плоской кривой?
2. Что называется средней кривизной дуги плоской кривой?
3. Что называется кривизной дуги в точке?
4. Что называется радиусом кривизны?
5. Какие точки плоской кривой называются точками спрямления?
6. По какой формуле вычисляется кривизна линии, заданной уравнением 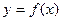 ?
?
7. По какой формуле вычисляется кривизна линии, заданной уравнением  ?
?
8. Что называется центром кривизны плоской кривой?
9. Что называется кругом кривизны плоской кривой?
10. Что называется эволютой?
11. Какая кривая называется эвольвентой?
12. Что называется кривизной пространственной кривой?
13. По какой формуле вычисляется кривизна пространственной кривой  ?
?
14. Что называется кручением пространственной кривой?
15. По какой формуле вычисляется кручение пространственной кривой  ?
?
16. Что называется тангенциальным единичным вектором пространственной кривой  ? По какой формуле он вычисляется?
? По какой формуле он вычисляется?
17. Что называется единичным вектором главной нормали пространственной кривой  ? По какой формуле он вычисляется?
? По какой формуле он вычисляется?
18. Что называется единичным вектором бинормали пространственной кривой  ? По какой формуле он вычисляется?
? По какой формуле он вычисляется?
19. Что представляет собой сопровождающий трехгранник пространственной кривой?
20. Какие векторы образуют соприкасающуюся плоскость, нормальную плоскость и спрямляющую плоскость?
Практические задания, выполняемые на занятии
23.1. Найти кривизну линии 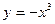 в точке с абсциссой
в точке с абсциссой 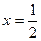 .
.
23.2. Найти координаты центра кривизны линии  в точке
в точке  .
.
23.3. Найти тангенциальный единичный вектор 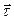 кривой
кривой 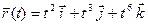 в точке
в точке  .
.
23.4. Найти тангенциальный единичный вектор 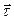 кривой
кривой 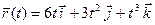 в точке
в точке  .
.
23.5. Найти единичный вектор бинормали 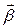 кривой
кривой 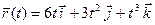 в точке
в точке  .
.
23.6. Найти единичный вектор главной нормали 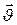 кривой
кривой 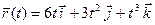 в точке
в точке  .
.
23.7. Найти кривизну и кручение кривой 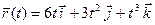 в точке
в точке  .
.
23.8. Составить уравнение соприкасающейся плоскости кривой 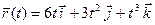 в точке
в точке  .
.
23.9. Составить уравнение спрямляющей плоскости кривой 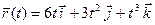 в точке
в точке  .
.
23.10. Составить уравнение нормальной плоскости кривой 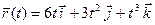 в точке
в точке  .
.
Задания для самостоятельной работы
23.11. Найти радиус кривизны эллипса  в точке
в точке 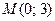 .
.
23.12. Найти координаты центра кривизны линии 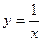 в точке
в точке  .
.
23.13. Найти тангенциальный единичный вектор 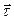 кривой
кривой 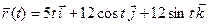 в произвольной точке.
в произвольной точке.
23.14. Найти тангенциальный единичный вектор 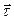 винтовой линии
винтовой линии 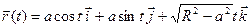 ,
, 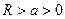 в произвольной точке.
в произвольной точке.
23.15. Найти единичный вектор бинормали 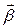 винтовой линии
винтовой линии 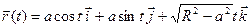 ,
, 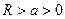 в произвольной точке.
в произвольной точке.
23.16. Найти единичный вектор главной нормали 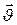 винтовой линии
винтовой линии 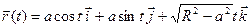 ,
, 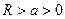 в произвольной точке.
в произвольной точке.
23.17. Найти кривизну и кручение винтовой линии 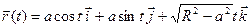 ,
, 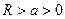 .
.
23.18. Составить уравнение соприкасающейся плоскости винтовой линии 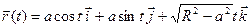 ,
, 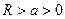 в произвольной точке.
в произвольной точке.
23.19. Составить уравнение спрямляющей плоскости винтовой линии 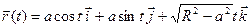 ,
, 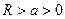 в произвольной точке.
в произвольной точке.
23.20. Составить уравнение нормальной плоскости винтовой линии 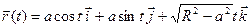 ,
, 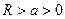 в произвольной точке.
в произвольной точке.
Литература
1. Бугров Я.С, Никольский С. М. Сборник задач по высшей математике: Учеб. пособие. – 4-е изд. – М.: ФИЗМАТЛИТ, 2001. – 304 с.
2. Высшая математика: Учебник / Г. Л. Луканкин, Н.Н. Мартынов, Г.А. Шадрин, Г.Н. Яковлев; Под. ред. Г.Н. Яковлева – 2-е изд., перераб. и доп. – М.: Высш. шк., 2004. – 584с.
3. Гусак А.А. Высшая математика. В 2-х т. Т.1.: Учебное пособие для студентов вузов. – Мн.: ТетраСистемс, 2001. – 544с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.I Учеб. пособие для втузов. – М.: Высш. шк., 1997. – 304 с.
5. Дюженкова Л.И. Практикум по высшей математике: учебное пособие в 2 частях. / Л.И. Дюженкова, О.Ю. Дюженкова, Г.А. Михалин. – М.: Бином. Лаборатория знаний, 2009.
6. Письменный Д.Т. Конспект лекций по высшей математике: полный курс. – М.: Айрис-пресс, 2009. – 608 с.
7. Письменный Д., Федин С., Шевченко Ю., Лунгу К. Сборник задач по высшей математике. 1 курс. – М.: Айрис-пресс, 2009. – 576 с.
8. Щипачев В.С. Задачник по высшей математике: Учеб. Пособие для вузов / В.С. Шипачев. – М.: Высш. шк., 2003. – 304 с.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!