
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выяснить, являются ли векторы линейно зависимыми, ,
|
|
|
|
План.
План.
План.
1. Формулы Крамера.
2. Метод обратной матрицы.
3. Метод Гаусса.
Методические рекомендации к занятию. При изучении материала темы следует освоить матричную форму записи заданной системы n линейных уравнений с n переменными и уметь переходить к этой форме от общего вида системы и наоборот. Необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными. Надо твердо уяснить, что вопрос о разрешимости системы n линейных уравнений с n переменными устанавливается с помощью теоремы Крамера, решаются же такие системы различными способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса. Наиболее важен для практики метод Гаусса, имеющий по сравнению с другими способами решения ряд достоинств: он менее трудоемок, позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число её решений: одно или бесконечно много.
Контрольные вопросы
1. Что называется системой линейных уравнений?
2. Что называется решением системы линейных уравнений?
3. Какая система линейных уравнений называется совместной (несовместной)?
4. Какая система линейных уравнений называется определенной (неопределенной)?
5. Какая матрица называется основной матрицей системы?
6. Какая матрица называется расширенной матрицей системы?
7. В каком случае система линейных уравнений имеет одно решение? По каким формулам оно находится?
8. В каком случае формулы Крамера для решения системы линейных уравнений неприменимы?
9. Как составить матричную форму системы линейных уравнений?
|
|
|
10. В каком случае систему линейных уравнений нельзя решить методом обратной матрицы?
Практические задания, выполняемые на занятии
3.1. Решить систему линейных уравнений по формулам Крамера и методом обратной матрицы.
a) 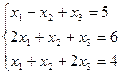 ; б)
; б) 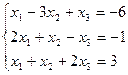 ; в)
; в)  .
.
3.2. Решить систему уравнений методом Гаусса.
а) 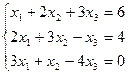 ; б)
; б) 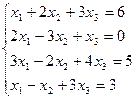 ;
;
в) 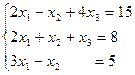 ; г)
; г)  .
.
Задания для самостоятельной работы
3.3. Решить систему линейных уравнений по формулам Крамера и методом обратной матрицы, методом Гаусса.
а) 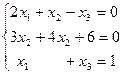 ;б)
;б)  ; в)
; в)  .
.
3.4. Решить систему уравнений методом Гаусса.
а)  ; б)
; б) 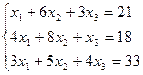 ;
;
в) 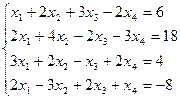 ;г)
;г) 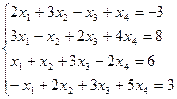 .
.
Практическое занятие № 4 (2 часа).
Тема: Система m линейных уравнений с n неизвестными.
1. Теоремы о совместных системах линейных уравнений.
2. Алгоритм нахождения базисного решения.
Методические рекомендации к занятию. При изучении данной темы необходимо повторить решение систем линейных уравнений методом Гаусса, последовательность действий по приведению матрицы к ступенчатому виду. На основании теоремы Кронекера-Капелли научиться устанавливать, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число её решений: одно или бесконечно много. В случае наличия у системы бесконечного числа решений необходимо определить число базисных решений.
Контрольные вопросы
1. Что является условием совместности системы линейных уравнений?
2. Что является условием определенности и неопределенности совместных систем линейных уравнений?
3. Приведите пример системы из трех линейных уравнений с тремя неизвестными, которая: а) имеет единственное решение; б) имеет бесконечно много решений; в) не имеет решений.
Практические задания, выполняемые на занятии
4.1. Решить систему уравнений методом Гаусса.
а)  ;
;
б)  .
.
4.2. Найти базисные решения системы уравнений
а) 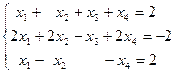 ; б)
; б) 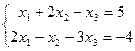 ; в)
; в)  .
.
Методика решения.
1. Составить расширенную матрицу системы и найди её ранг. Для этого необходимо привести матрицу к ступенчатому виду, а ранг ступенчатой матрицы равен числу строк в ней.
|
|
|
2. Если ранг меньше числа переменных, то система имеет бесконечно много решения. Число базисные переменных равно рангу, оставшиеся переменные – свободные. Общее число базисные решений не превосходит числа 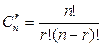 .
.
3. Проверяем все возможные наборы переменных на базисность: определитель из коэффициентов при этих переменных должен быть отличен от нуля.
4. Определяем свободные переменные. Придавая свободным переменным нулевые значения находим базисные решения.
4.3. Найти базисное решение для системы линейных уравнений
а) 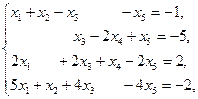 (одна из свободных переменных
(одна из свободных переменных 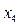 );
);
б) 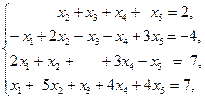 (одна из свободных переменных
(одна из свободных переменных 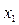 ).
).
Задания для самостоятельной работы
4.4. Решить систему уравнений методом Гаусса.
а) 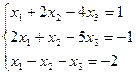 ; б)
; б) 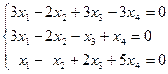 ; в)
; в)  .
.
4.5. Найти базисные решения системы уравнений
а) 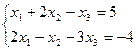 ; б)
; б)  ; в)
; в) 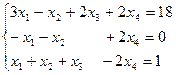 .
.
4.6. Найти базисное решение для системы линейных уравнений
а) 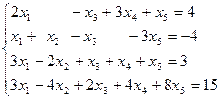 ; б)
; б)  .
.
Практическое занятие № 5 (2 часа).
Тема: Векторы. Векторное пространство.
1. n-мерный вектор. Линейные операции над векторами. n-мерное векторное пространство.
2. Размерность и базис векторного пространства.
3. Переход к новому базису.
4. Линейный оператор. Собственные значения и собственные векторы линейного оператора.
Методические рекомендации к занятию. В школьном курсе математики рассматривалось понятие вектора как направленного отрезка, т.е. множества точек, заключенных между двумя точками прямой с указанным направлением. Там же определялись операции над векторами (сложение, вычитание, умножение вектора на число), вводились координаты и понятие длины вектора.
Множества всех плоских и пространственных векторов, для которых определены операции сложения и умножения, а также умножения вектора на число, являются простейшими примерами векторных пространств. В данной теме обобщается понятие вектора и дается определение векторного пространства.
Следует отметить, что понятие линейной комбинации, линейной зависимости и независимости векторов вводится точно так же, как и для строк (столбцов) матрицы. Нужно четко уяснить понятие базиса n-мерного пространства, представляющего совокупность его линейно независимых векторов. При этом любой вектор пространства может быть представлен единственным способом в виде линейной комбинации векторов базиса.
|
|
|
В линейном (векторном) пространстве вводится метрика, т.е. способ измерять длины и углы. Это можно сделать, если ввести понятие скалярного произведения n-мерных векторов.
Одним из ключевых понятий данной темы является понятие «линейного оператора». Здесь необходимо понимать, что каждому линейному оператору соответствует матрица в данном базисе, и всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.
Контрольные вопросы
1. Что называется вектором?
2. Какие линейные операции над векторами вы знаете?
3. Что называется n-мерным вектором?
4. Что называется линейной комбинацией векторов?
5. Какие векторы называются линейно зависимыми, а какие линейно независимыми?
6. Какие векторы образуют базис линейного пространства?
7. Что называется разложением вектора по координатам в базисе?
8. Как выражается связь между координатами вектора в «старом» и «новом базисе»?
9. Что называется евклидовым пространством?
10. Какой базис называется ортонормированным?
11. Что называется оператором (преобразованием, отображением)?
12. Какой оператор называется линейным?
13. Что называется собственным значением линейного оператора?
14. Что называется собственным вектором линейного оператора?
15. Как находится собственное значение линейного оператора?
16. Как находится собственный вектор линейного оператора?
Практические задания, выполняемые на занятии
5.1. Выяснить, является ли вектор 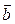 линейной комбинацией векторов
линейной комбинацией векторов 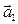 ,
,  ,
, 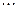 ,
, 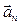 :
:
а) 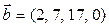 ,
,  ,
,  ,
, 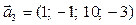 ;
;
б) 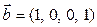 ,
, 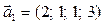 ,
, 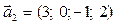 ,
,  ,
, 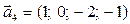 .
.
Методика решения.
Для выяснения линейной зависимости или независимости векторов необходимо составит линейную комбинацию этих векторов. Если существует нетривиальная линейная комбинация этих векторов, равная нулю, то векторы линейно зависимы, в противном случае векторы линейно независимы.
5.3. Показать, что векторы  ,
, 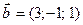 ,
,  , заданные в базисе
, заданные в базисе 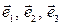 , сами образуют базис.
, сами образуют базис.
Методика решения.
Так как базисом n-мерного пространства называется совокупность n линейно независимых векторов, то необходимо исследовать векторы  ,
, 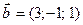 ,
,  на линейную зависимость.
на линейную зависимость.
|
|
|
5.4. Даны векторы 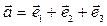 ,
, 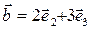 ,
, 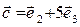 , где
, где 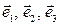 – базис линейного пространства. Доказать, что векторы
– базис линейного пространства. Доказать, что векторы 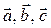 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 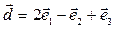 в базисе
в базисе 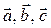 .
.
5.5. Линейный оператор  в базисе
в базисе 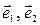 задан матрицей
задан матрицей 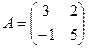 . Найти образ
. Найти образ 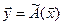 , где
, где 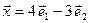 .
.
5.6. Линейный оператор  в базисе
в базисе 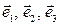 задан матрицей
задан матрицей 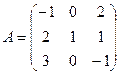 . Найти образ
. Найти образ 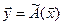 , где
, где 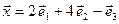 .
.
5.7. В базисе 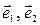 оператор
оператор  имеет матрицу
имеет матрицу  . Найти матрицу оператора
. Найти матрицу оператора  в базисе
в базисе 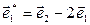 ,
, 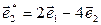 .
.
5.8. Найти собственные значения и собственные векторы линейных операторов, заданных матрицами:
а) 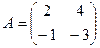 ; б)
; б)  .
.
Задания для самостоятельной работы
5.9. Выяснить, является ли вектор 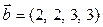 линейной комбинацией векторов
линейной комбинацией векторов 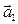 ,
,  ,
, 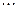 ,
, 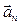 :
:
а) 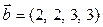 ,
, 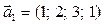 ,
, 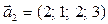 ,
,  ;
;
б) 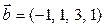 ,
,  ,
, 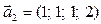 ,
, 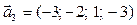 .
.
5.10. Показать, что векторы 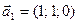 ,
, 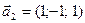 ,
,  , заданные в базисе
, заданные в базисе 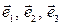 , сами образуют базис. Найти координаты вектора
, сами образуют базис. Найти координаты вектора 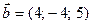 в базисе
в базисе  ,
, 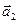 ,
, 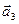 .
.
5.11. Линейный оператор  в базисе
в базисе 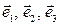 задан матрицей
задан матрицей 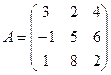 . Найти образ
. Найти образ 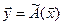 , где
, где  .
.
5.12. В базисе 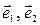 оператор
оператор  имеет матрицу
имеет матрицу 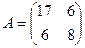 . Найти матрицу оператора
. Найти матрицу оператора  в базисе
в базисе 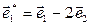 ,
, 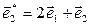 .
.
5.13. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей  .
.
Практическое занятие № 6 (2 часа).
Тема: Векторное и смешанное произведения векторов.
Прямая на плоскости.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1052; Нарушение авторских прав?; Мы поможем в написании вашей работы!