
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип суперпозиции
|
|
|
|
Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
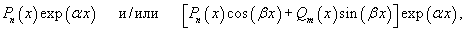
то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
Вопрос 11. Определение частного решения линейного неоднородного диф. уравнения 2-го порядка методом вариации произвольных постоянных(метод Лагранжа).
Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами b, c:
y''(x) + by'(x) + cy(x) = 0. (1)
Уравнение (1) имеет частное решение вида y(x) = 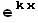 . Коэффициент k удовлетворяет алгебраическому уравнению второго порядка
. Коэффициент k удовлетворяет алгебраическому уравнению второго порядка
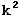 + bk + c = 0, (2)
+ bk + c = 0, (2)
которое возникает после подстановки функции y(x) = 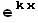 в уравнение (1). Уравнение (2) имеет либо два различных корня
в уравнение (1). Уравнение (2) имеет либо два различных корня 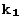 ,
, 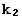 , либо один кратный корень
, либо один кратный корень 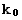 .
.
В первом случае линейно независимые решения уравнения (1) имеют вид
y(x) = 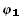 (x) =
(x) =  , y(x) =
, y(x) = 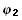 (x) =
(x) = 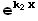 (3)
(3)
Во втором случае линейно независимыми решениями являются функции
y(x) = 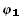 (x) =
(x) = 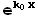 , y(x) =
, y(x) = 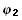 (x) = x
(x) = x 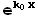 (4)
(4)
Линейная независимость решений означает, что не найдется такой константы С ≠ 0, что тождественно по x выполняется соотношение 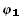 (x) = С
(x) = С 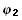 (x).
(x).
И в первом, и во втором случае общее решение уравнения (1) может быть записано в виде линейной комбинации
y(x) = 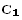
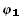 (x) +
(x) + 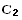
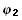 (x), (5)
(x), (5)
где 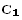 ,
, 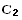 произвольные постоянные.
произвольные постоянные.
Метод вариации постоянных (метод Лагранжа) решения неоднородного дифференциального уравнения второго порядка
y''(x) + by'(x) + cy(x) = f(x) (6)
заключается в том, что решение уравнения (6) ищут в виде (5), но допускают зависимость 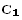 ,
, 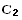 от независимой переменной x, т.е. в виде
от независимой переменной x, т.е. в виде
y(x) = 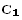 (x)
(x) 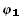 (x) +
(x) + 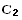 (x)
(x) 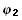 (x). (7)
(x). (7)
Найдем первую производную решения (7)
y'(x) = 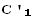 (x)
(x) 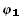 (x) +
(x) +  (x)
(x) 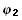 (x) +
(x) + 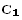 (x)
(x) 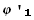 (x) +
(x) + 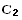 (x)
(x) 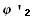 (x). (8)
(x). (8)
Потребуем, чтобы сумма первых двух членов в правой части формулы (8) была равна 0, т.е.
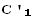 (x)
(x) 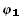 (x) +
(x) +  (x)
(x) 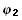 (x) = 0, (9)
(x) = 0, (9)
и, таким образом:
y'(x) = 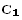 (x)
(x) 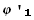 (x) +
(x) + 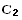 (x)
(x) 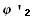 (x). (10)
(x). (10)
В силу (10) для второй производной функции y(x) имеем выражение
y''(x) = 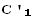 (x)
(x) 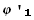 (x) +
(x) +  (x)
(x) 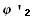 (x) +
(x) + 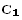 (x)
(x) 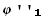 (x) +
(x) + 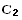 (x)
(x) 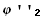 (x). (11)
(x). (11)
Подставляя (7), (10) и (11) в уравнение (6) и производя группировку членов, приходим к соотношению
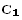 (x)(a(x)
(x)(a(x) 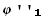 (x) + b(x)
(x) + b(x) 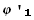 (x) + c(x)
(x) + c(x) 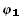 (x)) +
(x)) + 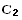 (x)(a(x)
(x)(a(x) 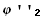 (x) + b(x)
(x) + b(x) 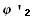 (x) + c(x)
(x) + c(x) 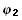 (x)) + a(x)(
(x)) + a(x)(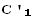 (x)
(x) 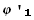 (x) +
(x) +  (x)
(x) 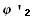 (x)) =f(x) (12)
(x)) =f(x) (12)
В силу того, что функции 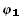 (x),
(x), 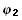 (x) решения линейного однородного уравнения (1), уравнение (12) принимает вид
(x) решения линейного однородного уравнения (1), уравнение (12) принимает вид
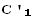 (x)
(x) 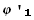 (x) +
(x) +  (x)
(x) 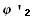 (x) = f(x) (13)
(x) = f(x) (13)
Таким образом, для функций 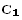 (x),
(x), 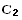 (x) справедлива следующая система дифференциальных уравнений первого порядка
(x) справедлива следующая система дифференциальных уравнений первого порядка
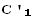 (x)
(x) 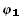 (x) +
(x) +  (x)
(x) 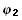 (x) = 0,
(x) = 0,
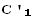 (x)
(x) 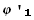 (x) +
(x) +  (x)
(x) 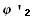 (x) = f(x) (14)
(x) = f(x) (14)
Из системы (14) можно найти, что
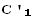 (x) =
(x) = 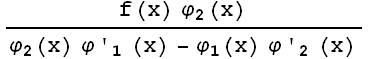 ,
,
 (x) =
(x) = 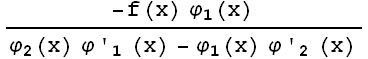 . (15)
. (15)
Из (15) функции 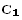 (x),
(x), 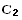 (x) находятся интегрированием.
(x) находятся интегрированием.
Если для уравнения (3) поставлена задача Коши, т.е. заданы начальные условия
y(0) = 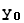 , y'(0) =
, y'(0) =  , (16)
, (16)
то для функций 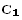 (x),
(x), 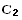 (x) можно написать формулы
(x) можно написать формулы
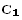 (x) =
(x) = 
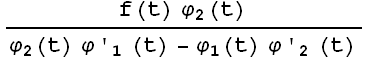 dt + α (17)
dt + α (17)
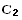 (x) =
(x) = 
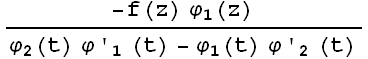 dt + β (18)
dt + β (18)
где α и β постоянные интегрирования. Они находятся подстановкой решения (7), в котором 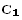 (x),
(x), 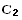 (x) задаются формулами (17), (18), в начальные условия (16). В результате получаются алгебраические уравнения для α и β:
(x) задаются формулами (17), (18), в начальные условия (16). В результате получаются алгебраические уравнения для α и β:
α 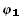 (0) + β
(0) + β 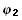 (0) =
(0) = 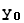 ,
,
α 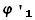 (0) + β
(0) + β 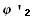 (0) =
(0) =  . (19)
. (19)
Решая их, находим α и β.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 403; Нарушение авторских прав?; Мы поможем в написании вашей работы!