Признак Даламбера сходимости ряда

Числовой ряд с положительными членами.

1)Числовой ряд 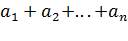называется рядом с положительными членами, если 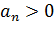при любом n.

2) Любой ряд с положительными членами либо сходится и его сумма есть положительное число, либо расходится и его сумма равна + .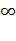

Доказательство: Пусть дан ряд с положительными членами 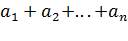. Запишем последовательность частичных сумм: S= 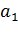; ; 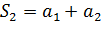; 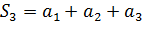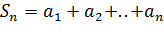. Таким образом, последовательность частичных сумм является строго возрастающей, но тогда возможны два случая:

1. Последовательность частичных сумм 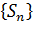ограничена сверху. Это ознчает что ряд сходится.

2. Последовательность частичных сумм 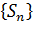возрастает неограниченно, тогда 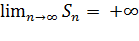ряд расходится.

Применять нужно, когда: 1. В общий член ряда входит какое-нибудь число в степени, например, 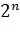, , 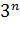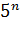и так далее. 2. В общий член ряда входит факториал.

Признак Даламбера: Рассмотрим положительный числовой ряд 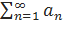. Если существует предел отношения последующего члена к предыдущему: 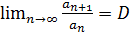, то:

а) При D < 1 ряд сходится. В частности, ряд сходится при D = 0.

б) При D > 1 ряд расходится. В частности, ряд расходится при D = .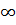

в) При D = 1 признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.

2) Интегральный признак сходимости ряда. Если f(x) – непрерывная, положительная и монотонно убывающая функция, то ряд 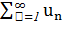где 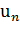= f(n) сходится или расзодится в зависимости от того, сходится или расходится интеграл .

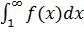Пример: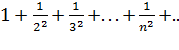

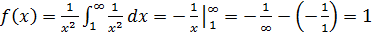– сходится интеграл, значит сходится и ряд.

Дата добавления: 2014-12-26