Знакочередующиеся ряды

Знакопеременные ряды

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрецательные.

Теорема. Если знакопеременный ряд 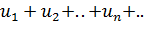таков что ряд составленный из абсолютных величин его членов, 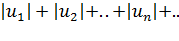сходится, то и данный знакопеременный ряд также сходится.

2) Абсолютная и условная сходимость

Ряд 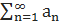называется абсолютно сходящимся, если ряд 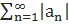также сходится.

Если ряд 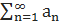сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд 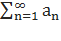называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.

a ₁ - a ₂ + a ₃ - a ₄ + a ₅ -...

2) Признак Лейбница

1.Ряд является знакочередующимся

2.Члены ряда убывают по модолю 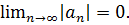Причем убыают монотонно. Если оба условия выполняются, то ряд сходится.

Дата добавления: 2014-12-26