Основные понятия. Область сходимости

Вопрос 27.Понятие степенного ряда. Теорема Абеля. Интервал сходимости.

Вопрос 26. Ряды с функциональными числами. Точка сходимости и область сходимости

Ряд, членами которого являются функции от х, называется функциональным:

.

Придавая определенное значение , получим числовой ряд

,

который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка х0 называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.

Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости.

В области сходимости функционального ряда его сумма является некоторой функцией от х: .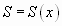

Определяется она в области сходимости равенством

, где

- частичная сумма ряда.

Определение 1.1. Степенным рядом называется функциональный ряд вида

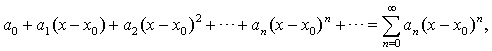(1.1)

где a₀, a₁, a₂, …,a_n,…, а также x₀ – постоянные числа. Точку x₀ называют центром степенного ряда.

Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида

(1.2)

Такой ряд всегда сходится при x =0 и, значит, его область сходимости есть непустое множество.

Теорема 1.1. (теорема Абеля). Если степенной ряд (1.2) сходится при некотором , где -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что Наоборот, если ряд (12) расходится при , то он расходится при всех значениях x таких, что

Доказательство. Пусть числовой ряд

(1.3)

сходится. Поэтому Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что 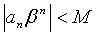для всех n =0,1,2,…

Рассмотрим теперь ряд

(1.4)

предполагая, что Так как и при этом то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда

(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.

Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.

Теорема Абеля позволяет дать описание области сходимости степенного ряда.

Теорема 1.2. Для степенного ряда (1.2) возможны только три случая:

1) ряд сходится в единственной точке x=0;

2) ряд сходится при всех значениях x;

3) существует такое R>0, что ряд сходится при всех значениях x, для которых и расходится при всех x, для которых

Определение 1.2. Интервал (-R,R), где число R определено в теореме 1.2, называется интервалом сходимости ряда (1.2), а число R – радиусом сходимости этого ряда.

Понятие радиуса сходимости будет распространяться на все три случая в теореме (3.2): для этого в случае 1 условимся считать R =0, а в случае 2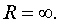

На практике радиус сходимости степенного ряда чаще всего определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда (1.2) отличны от нуля и существует предел Тогда радиус сходимости находится по формуле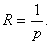

Действительно, в силу признака Даламбера ряд

сходится, если число

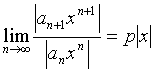
меньше 1, и расходится, если этот предел больше 1. Иначе говоря, ряд сходится для всех x таких, что и расходится при Это и означает, что число является радиусом сходимости ряда

Дата добавления: 2014-12-26