Енергетичні характеристики сигналів

Функціональний простір сигналів

Вибірка 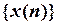лише в N точках повторює функцію 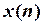. При зростанні N за рахунок зменшення кроку дискретизації T вибірка все ближче наближається до базового аналогового сигналу заданого на інтервалі 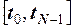, а відповідно точка N - вимірного векторного простору при 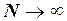займає деяке граничне положення. Тому, ми можемо говорити про функціональний простір сигналів. При 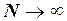вибірка переходить у функцію, що задана на відрізку 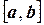, а сума переходить в інтеграл:

, .

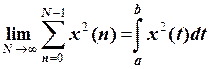Тоді норма сигналу згідно (2.5) дорівнює

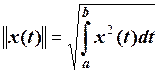. (2.10)

Метрика як відстань між сигналами і 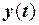згідно (2.6) дорівнює:

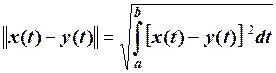. (2.11)

Скалярний добуток двох функцій згідно (2.7) визначається так:

. (2.12)

Кут між двома сигналами дорівнює:

. (2.13)

Відомі із фізики поняття потужності, енергії та середньої потужності електричного сигналу узагальнюють на аналогові сигнали довільної фізичної природи. Ці характеристики визначаються шляхом виконання певних математичних дій над функцією , яка є математичною моделлю сигналу:

1. Миттєва потужність сигналу :

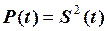. (2.14)

2. Енергія Е сигналу за час його дії на інтервалі :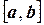

а) якщо дійсна функція,

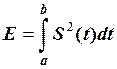; (2.15)

б) якщо комплексна функція,

, (2.16)

де – комплексно-спряжена функція до функції .

3. Середня потужність дійсного сигналу :

а) якщо скінчений сигнал (імпульс),

; (2.17)

б) якщо нескінчений періодичний сигнал з періодом ,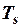

; (2.18)

в) якщо нескінчений неперіодичний сигнал,

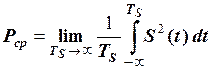. (2.19)

4. Середньоквадратичне (діюче) значення сигналу

. (2.20)

5. Взаємна енергія 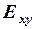двох сигналів та 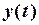на інтервалі :

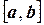а) якщо сигнали дійсні,

; (2.21)

б) якщо сигнали комплексні,

. (2.22)

6. Взаємна потужність двох сигналів та 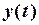на інтервалі часу :

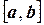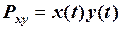, . (2.23)

Дата добавления: 2014-12-23