Гармонічні сигнали

Найчастіше гармонічний сигнал записують у вигляді косинусоїди. Її зручно записати наступним чином:

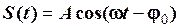, (2.29)

де А – амплітуда; 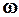– кругова частота, 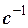; – початкова фаза.

Три константи А, , визначають все сімейство гармонік. Конкретним значенням цих констант відповідає конкретна гармоніка. У загальному випадку А, 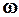і приймають будь-які значення із поля дійсних чисел.

Фазовий кут зручно вважати алгебраїчною величиною, що відповідає певному напрямку його відліку. При 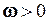напрямок осі часу t співпадає з напрямком фазового кута. Біжуча фаза гармоніки

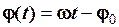. (2.30)

При 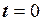біжуча фаза гармоніки є початковою:

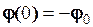. (2.31)

При значенні 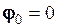косинусоїда незміщена. На рис. 2.8 вона зображена тонкою лінією. Якщо початкова фаза 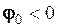, то 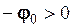, а це означає, що гармоніка 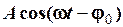випереджає гармоніку на величину (рис. 2.8). Зміщення при випередженні здійснюється проти напрямку осі t чи осі фазового кута .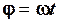

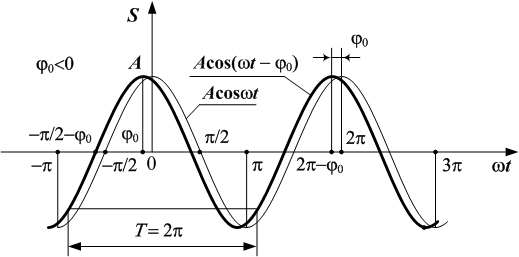
Рис. 2.8.

При 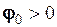, значення 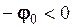і тоді, згідно (2.29), гармоніка 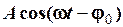запізнюється на . Теоретично гармоніка задана на всій числовій осі і не обмежена в часі. При зміні фазового кута 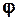на ціле число повних обертів вона повторює свої значення. Тому гармоніка періодична функція. У періодичної функції безліч періодів. Основний період 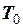, який є найменшим серед всіх додатних значень, визначається рівнянням

.

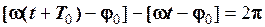Звідки

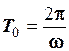. (2.32)

Достатньо знати кругову частоту 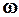, щоб визначити період .

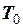Якщо ж задаватись періодом 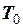, то можна знайти відповідну кругову частоту

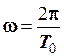. (2.33)

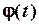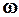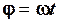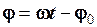Побудуємо графік біжучої фази . Згідно рівнянню (2.30) це лінійна функція при сталій круговій частоті . Графіки головного значення фазового кута гармоніки та фазового кута гармоніки 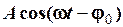зображено на рис. 2.9. Нагадаємо, що головне значення фазового кута лежить в межах 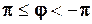, а .

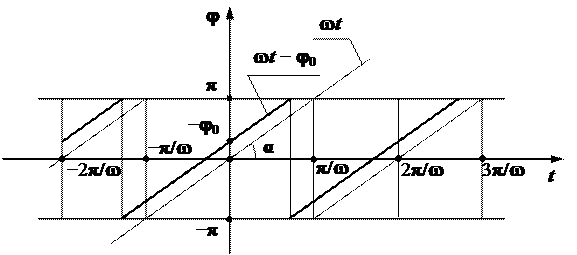Рис. 2.9.

Кутовий коефіцієнт обох біжучих фаз .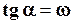

Тепер розглянемо синусоїду, яка іде із запізненням на кут :

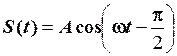. (2.34)

Графік цієї гармоніки зображено на рис. 2.10 і це є графік синусоїди.

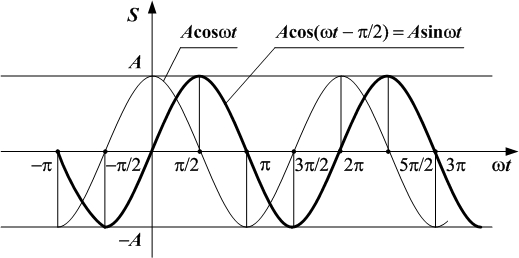
Рис. 2.10.

Дійсно

.

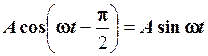Тому, гармоніку можна записувати і у вигляді синусоїди

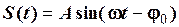. (2.35)

Синусоїда непарна функція: 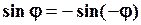. Отже, якщо аргументом гармоніки є фазовий кут 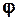, то вона є парною функцією, якщо розглядається як косинусоїда, або вона є непарною функцією, якщо розглядається як синусоїда. Ці твердження втрачають силу, якщо аргументом є час t, а початкова фаза 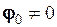. Дійсно, так як , то

.

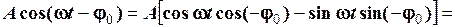
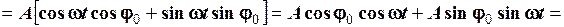
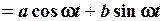Довільну косинусоїду представлено як суму незміщених косинусоїди та синусоїди. Змінивши знак аргументу t одержимо

.

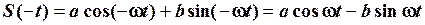Так як 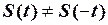та 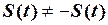, то це ні непарна, ні непарна функція. Аналогічним чином доводиться, що і зміщена синусоїда не є ні парною, ні непарною функцією.

Якщо початкова фаза 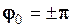, то 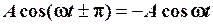. Це означає, що зміщення гармоніки на 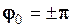рівносильне зміні знаку значення самої гармоніки. На рис. 2.11 зображена незміщена гармоніка 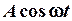та зміщена гармоніка 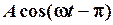. Ці дві гармоніки знаходяться в проти фазі. Практично цього ефекту можна одержати при зміні напрямку відліку амплітуди.

Дискретизований гармонічний сигнал одержують із аналогового

шляхом заміни неперервного часу дискретними відліками (рис. 2.12)

.

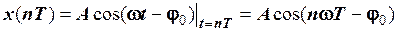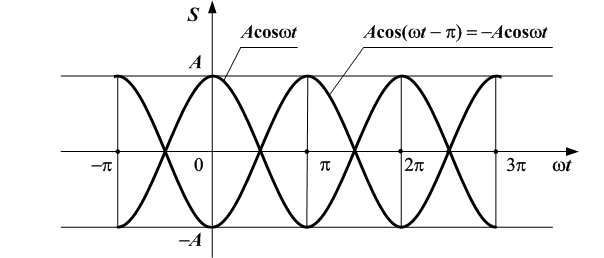
Рис. 2.11.

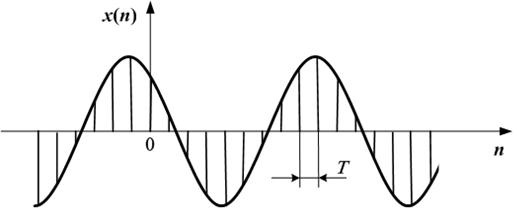
Рис. 2.12.

Одержали послідовність 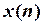, яка в точках повторює значення гармоніки.

Дата добавления: 2014-12-23