Функція одиничного стрибка

Функція одиничного стрибка, або функція вмикання, або функція Хевісайда аналітично описується виразом

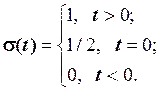(2.39)

Зміщена функція одиничного стрибка

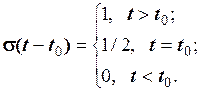(2.40)

Тут 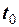− алгебраїчна величина, тобто це координата миттєвого стрибка функції (рис. 2.14).

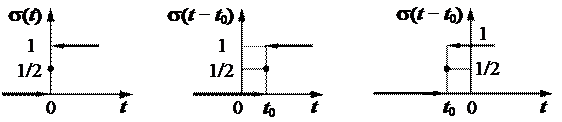Рис. 2.14.

Фізично функцію 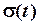реалізувати неможливо, бо неможливо здійснити миттєвий стрибок реального фізичного об’єкта. Але функцію 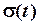можна розглядати як швидкий перехід сигналу з нульового рівня до одиничного значення за час 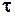при умові, що 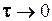(рис. 2.15).

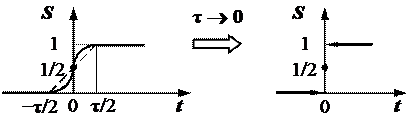Рис. 2.15.

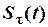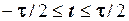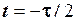Взагалі, перехідна неперервна функція на інтервалі може бути довільною, аби тільки її значення лежали в межах та вона мала полюс симетрії в точці з координатами (0, 1/2). Найпростішою серед цих перехідних функцій є лінійна. Хоча вона має скінчені розриви похідної в точках та 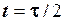, її фізична реалізація припустима.

Значення функції включення 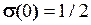є важливим лише в окремих випадках, тому функцію включення 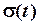на практиці розглядають в спрощеному вигляді. Замість формул (2.39) та (2.40) відповідно використовують такі формули

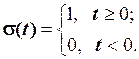(2.41)

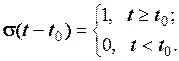(2.42)

При цьому спрощують і зображення s -функції (рис. 2.16).

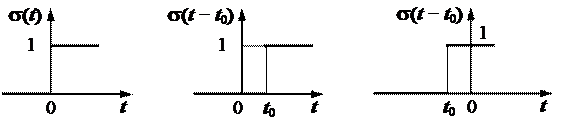Рис. 2.16.

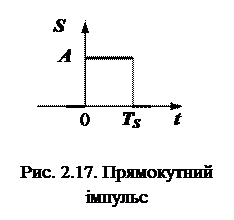Розглянемо прямокутний імпульс тривалістю 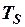(рис. 2.17). Він складається із трьох неперервних кусків. Математична модель цього імпульсу в аналітичній формі має вигляд

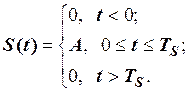
Використовуючи функцію одиничного стрибка, цей сигнал можна записати однією формулою

.

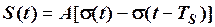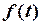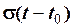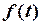При множенні сигналу на одержують сигнал , який повторює при 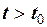(рис. 2.18).

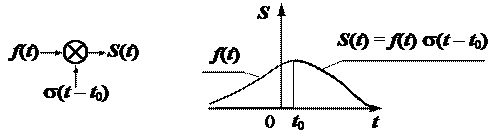Рис. 2.18.

Ось чому функцію 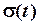ще називають функцією вмикання. Поки значення 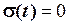, добуток 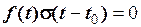, як тільки 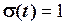функція 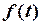потрапляє на вихід. 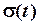проявляє себе як вимикач.

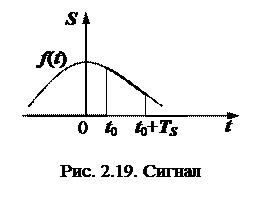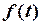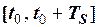Взагалі з допомогою функції Хевісайда можна з будь-якої функції виділити сигнал , який на відрізку повторює сигнал 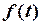(рис. 2.19).

.

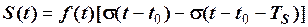Особливу роль в цифровій обробці сигналів відіграє дискретна функція одиничного стрибка.

Дата добавления: 2014-12-23