Розв’язування

.

Приклад 2.10. Задано трикутний імпульс напруги з амплітудою U. Тривалість імпульсу 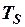(рис. 2.38). Обчислити енергію та відповідну норму заданого сигналу .

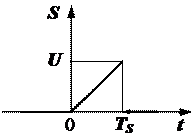
Розв’язування. Математичну модель сигналу запишемо у вигляді аналітичного виразу:

Енергія сигналу (імпульсу):

.

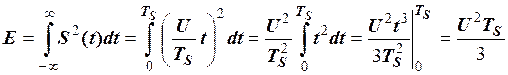Відповідна даній енергії норма імпульсу

.

Приклад 2.11. Визначити енергію та відповідну норму радіоімпульсу з прямокутною формою огинаючої. Радіоімпульс існує на інтервалі 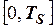і описується функцією .

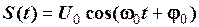Довідка. Для здійснення передачі сигналу на значні відстані без суттєвих втрат інформації, його помножують на високочастотну гармоніку 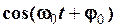, тобто передають у вигляді високочастотної гармоніки із змінною амплітудою . Після передачі сигналу 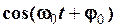, який називають радіоімпульсом, його фільтрують і знов одержують сигнал , який називають відеоімпульсом. Проілюструємо це у вигляді графіків (рис. 2.39).

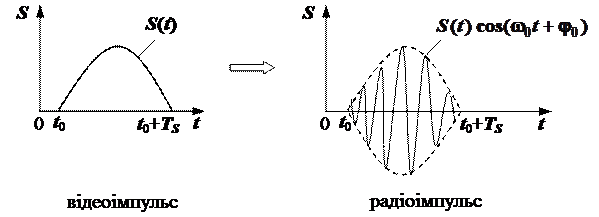Рис. 2.39.

Розв’язування. Так як радіоімпульс має сталу амплітуду U ₀, то він має прямокутну форму, що визначається огинаючими U = ± U ₀ (рис. 2.40).

Рис. 2.40.

Визначимо енергію радіоімпульсу:

.

Тут була здійснена заміна , тому , а . Якщо w ₀ достатньо велике, таке що 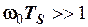, то енергія радіоімпульсу

.

Тобто значення енергії радіоімпульсу при високій частоті несучої гармоніки практично не залежить від початкової фази та самого значення . Звідси особлива роль енергетичної характеристики.

Норма радіоімпульсу

.

Зауваження. При визначенні інтегралу 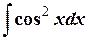скористались його табличним значенням.

Корисно запам’ятати, що

;

.

Приклад 2.12. Задано відеоімпульс 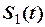у вигляді півперіоду синусоїди на відрізку 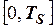, висота якого U (рис. 2.41).

		Підібрати амплітуду А прямокутного імпульсу тієї ж тривалості TS так, щоб відстань між двома сигналами та була мінімальною. Знайти при цьому кут між сигналами.

Рис. 2.41. Відеоімпульс

Розв’язування. Аналітичну форму сигналів запишемо у вигляді

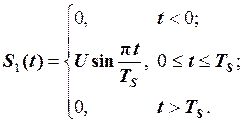
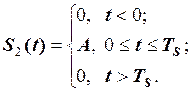
При визначенні 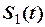на інтервалі була використана пропорція

.

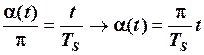Знайдемо квадрат відстані між сигналами:

.

Обчислимо кожний із трьох інтегралів окремо.

.

.

.

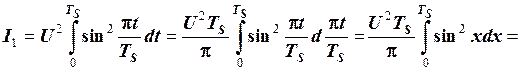
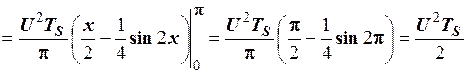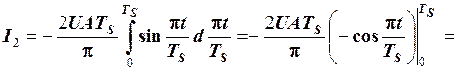
Отже,

. (1)

Умова мінімальної відстані в залежності від А має вигляд

.

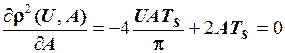Звідки

. (2)

Визначимо 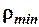, підставивши (1) в (2).

.

.

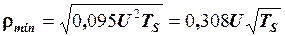Знайдемо енергію імпульсів:

;

;

.

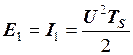Визначимо норми сигналів:

; .

Знайдемо кут між сигналами

.

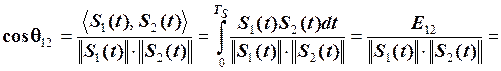
Отже, .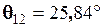

Приклад 2.13. Дано дві тривимірні вибірки: x (n)= (4; −4; 7)та y (n)= (3; −2; 6). Знайти відстань і кут між вибірками та складову вибірки х в напрямку вибірки у.

Розв’язування. Вибірку ототожнюємо із тривимірними векторами. Визначимо норми вибірок:

.

.

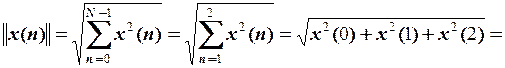
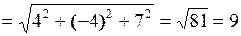Знайдемо відстань між вибірками як їх метрику

.

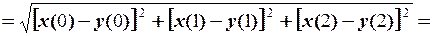
Скалярний добуток вибірок

.

Знайдемо кут між вибірками

.

Одиничний вектор в напрямку вибірки y:

.

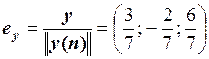Тому, складова вибірки x в напрямку вибірки y дорівнює:

.

Приклад 2.14. Сигнали 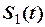та 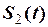прямокутні відеоімпульси з амплітудами А ₁ та А ₂, тривалості Т ₁ та Т ₂ зображені на рис. 2.42. Обидва сигнали одночасно відрізняються від нуля на інтервалі t. Визначити
кут між сигналами.

Рис. 2.42.

Розв’язування. Спочатку знайдено скалярний добуток сигналів:

.

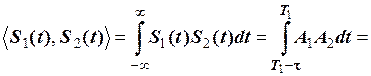
Визначимо норми сигналів:

;

.

Визначимо кут між сигналами:

.

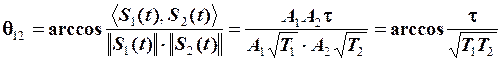Як бачимо, величина кута між прямокутними імпульсами не залежить від їх амплітуд А ₁ та А ₂.

Приклад 2.15. Задані два сигнали: прямокутний відеоімпульс та експоненціальний відеоімпульс 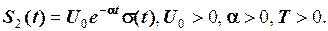Вважаючи тривалість Т прямо­кутного імпульсу фіксованою, визначити величину метрики .

Розв’язування. Знайдемо квадрат відстані між сигналами:

.

.

.

.

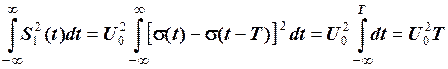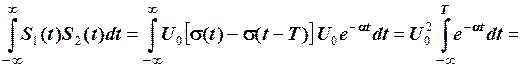
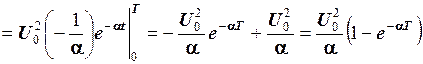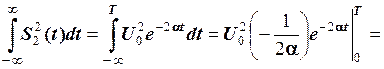
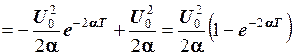Отже,

.

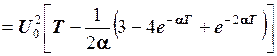Величина метрики як відстань між сигналами дорівнює

.

Дата добавления: 2014-12-23