Приклади

Приклад 2.1. Дано графічне зображення одиничного прямокутного імпульсу (рис. 2.28). Він має амплітуду А та тривалість 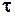. Записати в аналітичній формі математичну модель цього імпульсу та зміщених в сторону випередження та запізнення його копій.

		Розв’язування.З рисунку видно, що сигнал є кусково-неперервною функцією, що складається із трьох ділянок. Кожна ділянка має свій аналітичний вираз. Тому математична модель сигналу (1)

Рис. 2.28. Графік сигналу

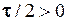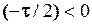Тут − додатне число, тому , . Запишемо загальну формулу зміщеного сигналу

(2)

При 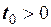сигнал йде із запізненням (рис. 2.29), а при 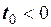− із випередженням (рис. 2.30).

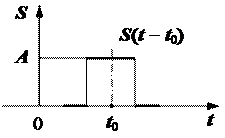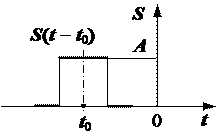Рис. 2.29. Графік сигналу Рис. 2.30. Графік сигналу

із запізненням із випередженням

Математичну модель незміщеного одиночного прямокутного імпульсу можна записати у вигляді єдиного аналітичного виразу, якщо використати функцію включення :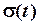

. (3)

Варто перевірити вірність цієї формули. Нагадуємо, що 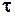− додатне число. Якщ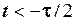о , то , а це означає, що . Тим більш , а тому також і 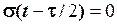. Отже, 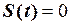, що відповідає рівнянню (1). Якщо 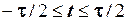, то , тому . А ось , тому 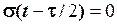. Підставляємо ці значення функції включення в формулу (3) одержимо, що . Це відповідає формулі (1). Нарешті, розглянемо випадок, коли 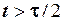. При цьому , тому , , тому . Тоді 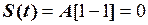. Отже, формула (3) відповідає формулі (1).

Для зміщених сигналів формула (3) набуває вигляду:

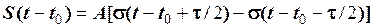, (4)

де 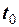− дійсне число. При 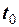> 0 мова йде про затримку сигналу, а при 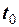< 0 − про випередження.

Приклад 2.2. Сигнал складається із трьох прямокутних одиничних імпульсів (рис. 2.31). Всі імпульси однакові, але зміщені між собою. Задати сигнал у вигляді аналітичного виразу.

Рис. 2.31. Графік сигналу

Розв’язування. Незміщений сигнал запишемо у вигляді

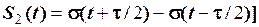. (1)

Тоді сигнал, що йде з випередженням

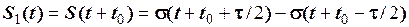, (2)

а сигнал, що йде з запізненням

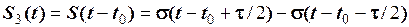. (3)

Отже, сигнал можна записати так

.

Використовуючи для запису зміщеного сигналу вираз 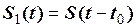, де 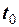вже алгебраїчна величина, дану суму можна записати достатньо компактно:

, (4)

де n = -1, 0, +1.

Значення n = -1 береться для сигналу 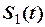, n = 0 − для сигналу , n = 1 − для сигналу .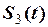

Приклад 2.3. На рис. 2.32 зображена періодична послідовність прямокутних одиничних імпульсів. Задати послідовність у вигляді аналітичного виразу.

Рис. 2.32. Графік імпульсів

Розв’язування. Скористаємося формулою (4) прикладу 2.2, враховуючи, що в даній задачі основний період 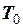дорівнює 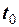. Отже

. (1)

Застосувавши функцію включення, математичну модель послідовності імпульсів вдалось записати у вигляді компактного аналітичного виразу.

Приклад 2.4. На рис. 2.33 зображені однакові відеоімпульси, що зміщені між собою. Незміщений відеоімпульс аналітично задається виразом

, (1)

де f (t) − деяка неперервна функція, на яку діють дві зміщені функції включення. Знаючи S (t), записати аналітичну формулу сигналів S ₁ (t) та S ₂ (t).

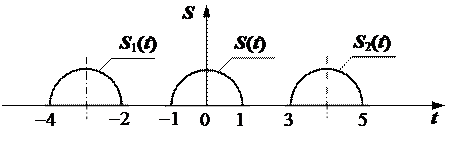Рис. 2.33. Графік відеоімпульсів

Розв’язування. В загальному випадку аналітичний вираз зміщеного сигналу повинен врахувати зміщення функції 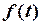, межі визначення якої не задані, та двох функцій включення.

Розглянемо спочатку сигнал 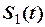. Координата осі цього відео імпульсу . Тому

.

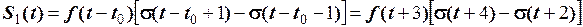Аналогічним чином розглядаємо сигнал . Тепер уже 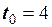. Тому

.

Приклад 2.5. Дано графічне зображення сигналу (рис. 2.34). Записати математичну модель в аналітичній формі як кусково-неперервну функцію, а потім у вигляді одного аналітичного виразу.

Рис. 2.34. Графік сигналу Рис. 2.35. Графік сигналу

Розв’язування. Функція кусково-неперервна, що має три характерні ділянки, аналітичні вирази яких мають вигляд:

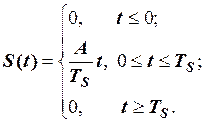
Рівняння на відрізку можна одержати із пропорції .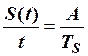

Задане графічне зображення (рис. 2.34) сигналу при 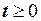подамо як суму двох лінійних сигналів 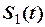та з однаковими за модулем, але різним за знаком значенням кута a (рис. 2.35).

Визначимо функції 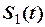та , використовуючи функцію вмикання:

, ;

, .

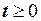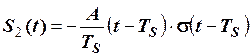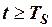Знаходимо функцію :

.

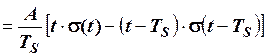Отже, сигнал поданий у вигляді одного аналітичного виразу.

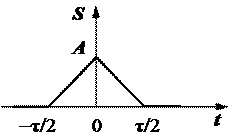Приклад 2.6. Відеоімпульс (рис. 2.36) має форму рівнобедреного трикутника і розміщений симетрично відносно початку відліку часу. Записати в аналітичній формі математичну модель цього відеоімпульсу та зміщених в часі його копій.

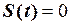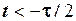Розв’язування. Якщо трикутний імпульс розглядати як кусково-неперервну функцію, то вона складається із чотирьох характерних ділянок. при , де 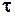− додатне число. При 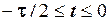сигнал є відрізком прямої, що з’єднує точку () та точку (0, А). Легко перевірити, що 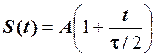відповідає цій умові. При сигнал є відрізком прямої, що з’єднує точку (0, А) та точку (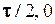). Це буде функція . На четвертій ділянці при сигнал 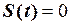. Таким чином математична модель кусково-неперервної функції задається виразом

(1)

Якщо використати функції включення, то аналітична модель трикутного імпульсу має вигляд

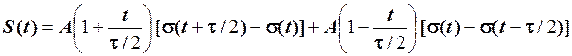. (2)

Розкриття дужок формули (2) не призведе до помітних спрощень.

Для зміщених сигналів формула набуває вигляду

(3)

,

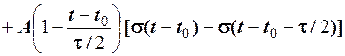де 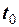− дійсне число. При 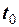> 0 мова йде про затримку сигналу, а при 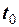< 0 − про випередження. Формула (3) визначена на всій осі часу.

Приклад 2.7. На рис. 2.37 зображена періодична послідовність трикутних імпульсів. Задати послідовність у вигляді аналітичного виразу.

Рис. 2.37. Графік сигналу

Розв’язування. Скористаємося формулою (3) прикладу 2.6. Параметр 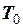− основний період послідовності. Послідовність запишемо у вигляді суми

(1)

.

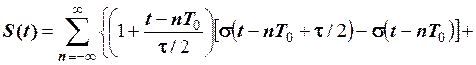
Отже, одержали аналітичний вираз періодичної послідовності трикутних імпульсів, що визначений на всій осі часу.

Приклад 2.8. Обчислити інтеграл .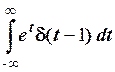

Розв’язування. Згідно фільтрувальній властивості дельта-функції

.

Так як 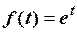, , то .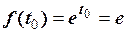

Отже,

.

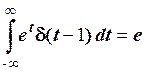Приклад 2.9. Обчислити інтеграл .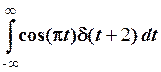

Дата добавления: 2014-12-23