РЕШЕНИЕ. Используя локальную теорему Лапласа, имеем

РЕШЕНИЕ.

Используя локальную теорему Лапласа, имеем

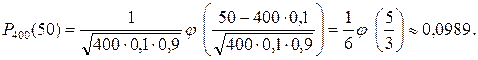
Задание 5. 2. Вероятность появления события за время испытаний P=0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз при 100 испытаниях.

Если вероятность появления события в независимых испытаниях постоянна и отлична от нуля и единицы, то вероятность того, что в n испытаниях событие произойдет от 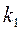до 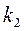раз определяется по формуле:

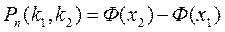
где Ф(х) - функция Лапласа.

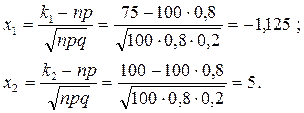
Учитывая, что функция Лапласа нечетна, т. е. Ф(-х)=-Ф(х), получим

P₁₀₀(75;90)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25).

По таблице (Приложение 2) найдем

Ф(5)=0,499; Ф(1,25)=0,394.

Искомая вероятность данного события равна

P₁₀₀(75; 90)=0,499+0,394=0,893.

б) требование, чтобы событие появилось не менее 75 раз, означает, что число появления события может быть равно 75, либо 76,..., либо 100. Таким образом, в рассматриваемом случае следует принять k₁=75, k₂=100. Тогда

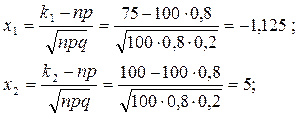
Ф(1,25)=0,394, Ф(5)=0,5.

Искомая вероятность равна

P₁₀₀(75; 100)=Ф(5)-Ф(-1,25)=0,5+0,394=0,894.

в) события «А появилось не менее 75 раз» и «А появилось не более 74 раз» противоположны, поэтому сумма вероятностей этих событий равна единице. Следовательно, искомая вероятность

P₁₀₀(0; 74)=1-P₁₀₀(75; 100)=1- 0,894=0,106.

Задание № 6.

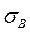По результатам контроля шлифованных шеек валов определить среднее значение параметра шероховатости , выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение 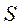для заданной выборки в предположении, что рассеивание значений параметра шероховатости подчиняется нормальному закону. Задавшись доверительной вероятностью определить доверительные интервалы для величины среднего значения параметра шероховатости 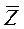и величины среднего квадратического отклонения .

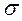№ детали в выборке	Значение параметра шероховатости Ra, мкм
1.	0,7i
2.	0,6j
3.	0,7j
4.	0,72
5.	0,76
6.	0,64
7.	0,6i
8.	0,70
9.	0,61
10.	0,8j

Теоретический материал для данного задания приводится в главе 10 [2.

Пример выполнения задания № 6.

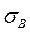По результатам контроля шлифованных шеек валов определить среднее значение параметра шероховатости , выборочное среднее квадратическое отклонение и исправленное выборочное среднее квадратическое отклонение 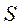для заданной выборки в предположении, что рассеивание значений параметра шероховатости подчиняется нормальному закону. Задавшись доверительной вероятностью определить доверительные интервалы для величин 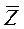и .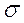

№ детали в выборке	Значение параметра шероховатости Ra, мкм
1.	0,75
2.	0,68
3.	0,78
4.	0,72
5.	0,76
6.	0,64
7.	0,60
8.	0,70
9.	0,61
10.	0,81

Дата добавления: 2014-12-26