РЕШЕНИЕ. 3 страница

Теперь необходимо осуществить проверку вида закона распределения. Это целесообразно делать с помощью критерия согласи Пирсона , так как объем выборки .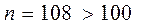

Статистикой критерия Пирсона служит величина

где: -количество наблюдений в каждом интервале;

- объем выборки;

- вероятность попадания случайной величины в -йинтервал.

Для того чтобы обеспечить удобство вычисления , необходимо произвести нормирование функции нормального распределения, то есть перейти к функции Лапласа. Функция Лапласа представляет интеграл с переменным верхним пределом вида

-

Для удобства его вычисления составляется таблицы:

№ интервала	Граница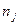
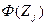
	12,80	35,26	24,03	-∞	-1,60	-0,500	-0,4450
	35,26	57,72	46,49	-1,60	-0,94	-0,4450	-0,3265
	57,72	80,18	68,95	-0,94	-0,28	-0,3265	-0,1105
	80,18	102,64	91,41	-0,28	0,38	-0,1105	0,1480
	102,64	125,10	113,87	0,38	1,04	0,1480	0,3510
	125,10	147,56	136,33	1,04	1,70	0,3510	0,4555
	147,56	170,00	158,78	1,70	+∞	0,4555	0,5000

№ интервала	Граница
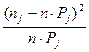
	12,80	35,26	0,0550	5,94000	1,0600	0,189
	35,26	57,72	0,1185	12,79800	0,2020	0,003
	57,72	80,18	0,2160	23,32800	-3,3280	0,475
	80,18	102,64	0,2585	27,91800	2,0820	0,155
	102,64	125,10	0,2030	21,92400	0,0760	0,000
	125,10	147,56	0,1045	11,28600	-0,2860	0,007
	147,56	170,00	0,0445	4,80600	0,1940	0,008
			1,00			0,84

В соответствии с таблицей приложения 5 [2] при значение 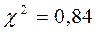дает с вероятностью 0,99 то, что нулевую гипотезу о том, что закон распределения является нормальным, следует принять.

Предельно допустимая концентрация в области рабочей зоны равна 300 мг/м³, но концентрация в 200 мг/м³, оказывает негативное воздействие на здоровье рабочего персонала. Поэтому необходимо определить вероятность возникновения такой концентрации.

Нормальный закон распределения является симметричным, поэтому дисперсия и среднее значение остаются прежними.

Итак:

, , .

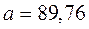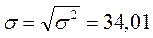Левой границей интервала будет значение 200, правой - 300. Переходим к функции Лапласа:

,

.

Значения функций Лапласа заданного аргумента находятся из таблицы приложения 2 [2]:

, ,

.

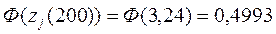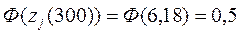Следовательно, .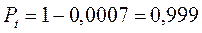

Как видно из примера, вероятность достижения концентрации гексана значения в пределах от 200 до 300 мг/м³, равная 0,0007 не велика, и можно сделать прогноз, что применение данного вида СОТС при сохранении текущих условий работы не будет вредным.

Задание № 8.

По заданным условиям (таблица 8.1), матрице планирования и результатов эксперимента (таблица 8.2) построить математическую модель в виде уравнения регрессии влияния режимов обкатывания заготовки роликом (продольной подачи S, мм/мин; скорости обкатки V, м/мин; усилия деформирования Р, кН,) на значение параметра шероховатости .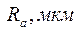

Таблица 8.1 - Условия эксперимента

Пределы варьирования	Факторы (обозначения)
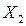
Продольная подача S, мм/мин,	Скорость обработки V, м/мин,	Усилие деформирования Р, кН,
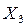
Основной уровень	0,3	25,3	2,5
Шаг варьирования	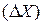0,1	12,2	0,8
Верхний уровень	0,4	37,5	3,0
Нижний уровень	0,2	13,1	2,0

Таблица 8.2 - Матрица планирования и результаты эксперимента

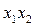
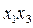
	+1	+1	+1	+1	+1	+1	0,9i
	-1	+1	+1	-1	-1	+1	0,8j
	+1	-1	+1	-1	+1	-1	0,8i
	-1	-1	+1	+1	-1	-1	1,1j
	+1	+1	-1	+1	-1	-1	1,2i
	-1	+1	-1	-1	+1	-1	1,2j
	+1	-1	-1	-1	-1	+1	1,4i
	-1	-1	-1	+1	+1	+1	1,3j
							1,2i
							1,3j
							1,2i
							1,3j

Теоретический материал для данного задания приводится в [5].

Наибольшее влияние на шероховатость поверхности при накатывании оказывают следующие параметры (факторы) (режимы обработки): продольная подача S,мм/об, скорость обработки V,м/мин., усилие деформирования Р, кН.

Предлагается алгоритм построения регрессионных моделей влияния указанных режимов обработки на достигаемую шероховатость обрабатываемых поверхностей осей, путем статистического анализа экспериментальных данных.

Порядок модели до реализации эксперимента неизвестен. В этом случае применяется последовательное планирование эксперимента, т.е. используется свойство композиционности. Это свойство плана позволяет разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к сложным, используя результаты предыдущих опытов.

На первом этапе выдвигается гипотеза о линейности уравнения регрессии, т.е.

.

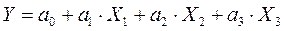На основе данных, полученных в результате реализации эксперимента, проверяется адекватность линейной модели. Если линейная модель неадекватна, то выдвигается гипотеза о значимом влиянии парных взаимодействий факторов:

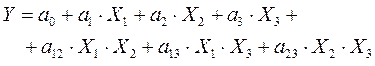
Вычисляются параметры данной модели и производится проверка ее адекватности. Если модель такого типа неадекватна, то выполненные ранее опыты дополняют новой серией, позволяющей вычислить коэффициенты модели квадратичной типа:

где 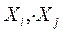- значения i-го и; j-го параметров режима поверхностного пластического деформирования (ППД); 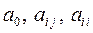- коэффициенты уравнения; i, j - номера факторов (параметров режима ППД), i=j; i,j = 1, 2, 3 (Р, S, V).

Для упрощения обработки результатов эксперимента факторы (параметры режима обработки ППД) нормализуют по формуле:

где 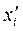- нормализованное значение фактора , на верхнем или нижнем уровне;

- действительное значение фактора;

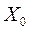- значение фактора на основном уровне;

- интервал варьирования i-го фактора.

Верхний уровень нормализованного фактора равен (+1), нижний - (-1), а основной нулю.

Эксперимент, в котором используют все возможные сочетания уровней, называется полным факторным экспериментом (ПФЭ). При числе уровней каждого фактора равном двум, число опытов ПФЭ составляет N = 2^k.

В рассматриваемом случае N = 2³ = 8. Вычисление параметров нормализованной линейной модели производится по формулам:

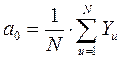
где 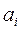- параметр нормализованной модели (i= 1, 2, 3...k);

k- число контролируемых факторов;

u - номер опыта (или серии опытов) (u = 1, 2, 3,..., N);

N - число опытов (или серий параллельных опытов);

Y_u - значение функции отклика в u-м опыте;

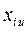- значение в u-oм опыте.

Все параметры линейной модели определяются с одинаковой дисперсией:

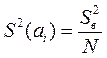
где - дисперсия воспроизводимости.

Если в каждой серии проводилось по mпараллельных опытов, то

где N - число серий опытов в плане; u - номер серии опытов;

j - номер параллельного опыта в серии;

Y_u - среднее значение отклика в u-й серии.

Если параллельные опыты отсутствуют, то для определения дисперсии воспроизводимости в центре плана проводится серия из m параллельных опытов.

Тогда

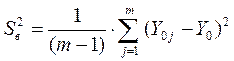
где - значение функции отклика (исследуемой характеристики шероховатости) в j-ом опыте серии (j=1, 2, 3,..., m);

- среднее арифметическое значение для .

Доверительный интервал для параметров линейной модели

где - значение критерия Стьюдента,

Р - заданный уровень достоверности значений .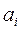

Для рассматриваемого случая

.

Параметр считается статистически значимым, если его абсолютная величина больше доверительного интервала: . Статистически незначимые параметры считаем равными нулю.

В зависимости от наличия сведений о дисперсии воспроизводимости эксперимента проверку адекватности уравнения регрессии можно производить по двум схемам. Первая из них применяется при отсутствии оценки дисперсии воспроизводимости, что характерно для пассивного эксперимента, и состоит из следующих этапов:

- вычисление дисперсии относительно среднего значения параметра оптимизации (остаточной дисперсии для уравнения нулевого порядка):

;

- расчет дисперсии, характеризующей отклонение экспериментальных значений величин от найденных по уравнению регрессии. Если порядок уравнения заранее неизвестен, то в случае многофакторного пространства начинают с уравнения первого порядка:

где 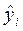- значение параметра, вычисленное по уравнению регрессии для условий i-ro опыта;

f=N-g - число степеней свободы;

g - число коэффициентов регрессии; для линейного уравнения g = k+1;для неполного квадратного уравнения, включающего члены типа и , 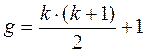;для полного квадратного уравнения ;

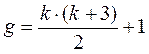k - число факторов;

- расчет отношения указанных дисперсий:

Если то модель неадекватна. Здесь и - числа степеней свободы.

Затем вычисляют коэффициенты уравнения регрессии в виде полинома первой степени (линейная модель). Для этого уравнения определяют значение и вычисляют отношение:

Затем проверяют значимость этого отношения . Если и новая модель неадекватна, переходят к модели более высокого порядка. Процедуру повторяют до тех пор, пока не будет выполнено условие .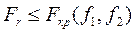

Индекс г соответствует степени предпоследнего полинома.

Если известна дисперсия воспроизводимости эксперимента, для оценки адекватности модели вначале рассчитывают дисперсию адекватности

,

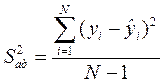а затем определяется расчетное значение критерия :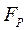

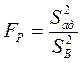
Если 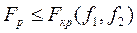, модель считается адекватной для принятой доверительной вероятности Р,чисел степеней свободы дисперсии адекватности , и дисперсии воспроизводимости . В противном случае модель неадекватна.

В данном случае дисперсия вопроизводимости 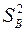известна. Число степеней свободы дисперсии адекватности при k = 3:

- для линейной модели:

;

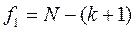- для модели, учитывающей парные взаимодействия:

;

- для модели учитывающей квадратичный характер зависимости:

.

Число степеней свободы для дисперсии воспроизводимости 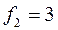. Вычисление параметров нормализованной модели с парными и тройными взаимодействиями производится по формулам:

;

;

.

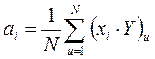Проверка статистической значимости параметров математической модели линейного типа и ее адекватности проводится так же, как и модели квадратичной зависимости.

Если линейная модель и модель с парными зависимостями неадекватны, в план проведенных опытов, который называется «ядром» эксперимента, добавляется некоторое количество специальным образом расположенных точек. Добавленные, или «звездные» точки плана находятся на расстоянии «звездного» плеча 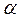от центра плана. Общее число опытов , при k факторах (в нашем случае k = 3)

,

где N - число опытов «ядра» плана (N = 8);

2z- число «звездных» точек (2z=2 - 3 = 6);

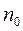- число опытов в центре плана.

Ортогональность плана заключается в выборе такого количества точек факторного пространства для измеряемого отклика, которое приводит к упрощению вычисления параметров модели. В этом случае значения каждого параметра модели вычисляются независимо от значений других параметров.

Значения параметров модели квадратичного типа вычисляются по формулам:

,

где 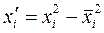. При 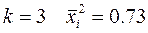, тогда .

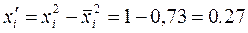В числителе формул находятся суммы значений функции отклика и значений нормализованного фактора в соответствующем столбце, а в знаменателе - сумма квадратов значений нормализованных факторов из соответствующих столбцов.

Дисперсия оценок параметров модели определяется по формулам:

;

;

;

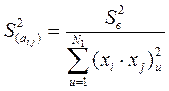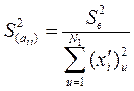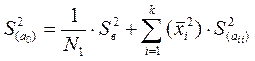
где - дисперсия воспроизводимости.

Доверительные интервалы для параметров модели в данном случае определяются при помощи критерия Стьюдента:

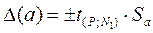
где 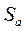- стандартное отклонение, рассчитанное для каждого из параметров модели.

Параметр математической модели считается статистически значимым, еcли соблюдается соотношение .

Пример выполнения задания № 8

Пусть условиям, матрица планирования и результатов эксперимента заданы таблицами 8.3 и 8.4.

Таблица 8.3 - Условия эксперимента

Пределы варьирования	Факторы (обозначения)
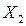
Продольная подача S, мм/мин,	Скорость обработки V, м/мин,	Усилие деформирования Р, кН,
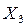
Основной уровень	0,3	25,3	2,5
Шаг варьирования	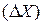0,1	12,2	0,8
Верхний уровень	0,4	37,6	3,0
Нижний уровень	0,2	13,1	2,0

Таблица 8.4 - Матрица планирования и результаты эксперимента

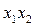
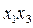
	+1	+1	+1	+1	+1	+1	0,9
	-1	+1	+1	-1	-1	+1	0,8
	+1	-1	+1	-1	+1	-1	0,8
	-1	-1	+1	+1	-1	-1	1,1
	+1	+1	-1	+1	-1	-1	1,2
	-1	+1	-1	-1	+1	-1	1,2
	+1	-1	-1	-1	-1	+1	1,4
	-1	-1	-1	+1	+1	+1	1,3
							1,2
							1,3
							1,2
							1,3

На первом этапе для поиска уравнения регрессии линейного типа был проведен полный факторный эксперимент типа 2³, состоящий из восьми опытов. Результаты реализации матрицы планирования эксперимента сведены в таблицу 8.4.

По результатам эксперимента вначале считаются параметры нормализованной линейной модели вида

,

где: ,

- нормализованное значение фактора на верхнем или нижнем уровне,

Дата добавления: 2014-12-26