РЕШЕНИЕ. 2 страница

При неудовлетворении этого условия, нулевую гипотезу отвергают и принимают альтернативную.

Для сравнение выборочного среднего с известным генеральным средним, используют критерий

.

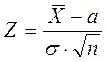Предполагается нормальное (логнормальное) распределение, однако в данном случае это требование является менее жестким.

Пусть при наличии большого объема экспериментальных данных были определены и .

Результаты исследований при несколько измененных условиях показали, что выборочные значения 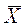и несколько отличаются от генеральных.

Требуется установить, имеется ли значимое различие между выборочным значением 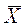и генеральным средним .

Решение этой задачи рассматривается для случаев, когда генеральная дисперсия 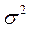известна и когда генеральная дисперсия 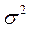неизвестна, но известна оценка . В качестве нулевой гипотезы принимается предположение о том, что . Генеральная дисперсия 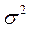сохранилась неизменной.

Нулевую гипотезу не отклоняют, если выполняется неравенство:

При альтернативе , (*)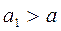

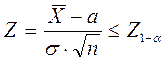При альтернативе ,

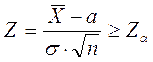
где и 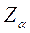- критические значения одностороннего критерия для уровня значимости .

При нарушении условий приведенных выше условий нулевую гипотезу отвергают и принимают альтернативную.

При альтернативной гипотезе 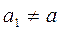используют двусторонний критерий значимости.

Если выполняется неравенство

,то нулевую гипотезу не отвергают.

Для сравнения двух средних значений нормально (логнормально) распределенных совокупностей используют критерий Стьюдента (Госсета)

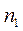Пусть из двух нормально распределенных генеральных совокупностей с неизвестными параметрами испытаны выборки объемом , и .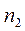

По результатам испытаний подсчитаны оценки параметров распределения .

Требуется проверить нулевую гипотезу о равенстве средних значений этих совокупностей, т.е. 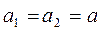,при альтернативной гипотезе .

Рассмотрим вначале случай, когда дисперсии генеральных совокупностей равны, т.е. 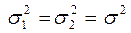(что может быть проверено по методике, изложенной выше - критерий Фишера).

Для проверки нулевой гипотезы 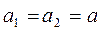вычисляют оценку дисперсии :

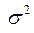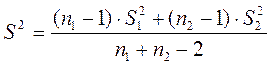
и статистику

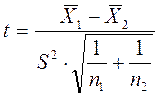
Статистику сопоставляют с критическим значением 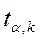, найденным для выбранного уровня значимости 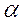и числа степеней свободы 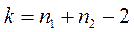из таблиц.

Если справедливо неравенство 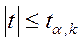то нулевую гипотезу не отвергают.

Если 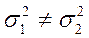, то равенство двух средних проверяют с помощью приближенного - критерия:

.

При этом число степеней свободы определяется из выражения:

,

где

Конечной целью любого статистического исследования является установление вида закона распределения изучаемой случайной величины, на основании которого можно прогнозировать поведение объекта или системы в дальнейшем.

В одних случаях закон распределения может быть установлен теоретически на основании выбранной модели рассматриваемого процесса. В других случаях функцию распределения выбирают априори.

Однако для получения надежных решений вероятностных задач в каждом отдельном случае необходима проверка соответствия опытных данных используемому закону распределения.

Одним из первых, наиболее простым, но весьма приближенным методом оценки согласия результатов эксперимента с тем или иным законом распределения является графический метод.

Опытные данные наносят на вероятностную бумагу и сравнивают с графиком принятой функции распределения, которая на вероятностной сетке изображается прямой линией. Если экспериментальные точки ложатся вблизи прямой со случайными отклонениями влево и вправо, то опытные данные соответствуют рассматриваемому закону распределения.

Систематические и значительные отклонения экспериментальных точек от аппроксимирующей прямой свидетельствуют об ошибочности принятой модели для обоснования закона распределения исследуемой случайной величины.

Графический способ в значительной степени является субъективным и используется на практике лишь в качестве первого приближения при решении этой задачи.

Существует большой ряд достаточно строгих аналитических критериев согласия результатов эксперимента выбранному ряду гипотетического распределения.

Однако при решении задач, связанных с исследованием характеристик (например, механических свойств) многие из них теряют свою универсальность в связи с тем, что параметры гипотетического распределения заранее неизвестны, и могут оцениваться лишь по результатам испытаний.

Если выбранный критерий согласия не позволяет сделать уверенный, однозначный вывод о соответствии опытных данных гипотетическому распределению, то необходимо провести проверку нулевой гипотезы по другому критерию.

Даже при очень больших объемах выборок (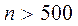) в ряде случаев нельзя отдать предпочтение какому-либо одному закону распределения. В этом случае выбор распределения решается удобством его применения в конкретной задаче.

Критерий согласия Пирсона (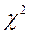) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению при большом объеме выборки ().

Критерий применим для любых видов функции даже при неизвестных значениях их параметров. В этом заключается его универсальность.

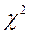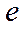Использование критерия предусматривает разбиение размаха варьирования выборки на интервалы и определение числа наблюдений (частоты) для каждого из интервалов,

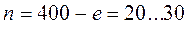Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Число интервалов зависит от объема выборки. Обычно принимают: при ; при ; при ; при .

Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако если число таких интервалов составляет менее 20% от их общего количества, допускаются интервалы с частотой 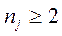. Статистикой критерия Пирсона служит величина:

где 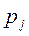- вероятность попадания изучаемой случайной величины в 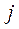-ый интервал, вычисляемая в соответствии с гипотетическим законом распределения .

При вычислении вероятности 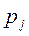нужно иметь в виду, что левая граница 1-го интервала и правая граница последнего должна совпадать с границами области возможных значений случайной величины. Например, при нормальной законе распределения правый интервал начинается в - , а последний простирается до .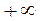

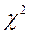определяют по соответствующей таблице для уровня значимости и числа степеней свободы 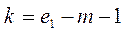, здесь e_l - число интервалов после объединения, 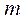- число параметров, оцениваемых по рассматриваемой выборке.

При несоблюдении неравенства 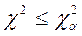принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.

Недостатком критерия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределения по критерию 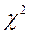другими критериями. Это необходимо при объеме выборки .

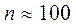Критерий согласия этот критерий используется при объемах выборки и является более мощным, чем критерий 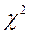, однако при его применении требуется больший объем вычислений.

Поэтому при 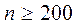этот критерий целесообразно использовать только в тех случаях, когда проверка гипотезы по другим критериям не приводит к безусловным выводам.

Критерий базируется на распределении статистики, представляющей собой взвешенную сумму квадратов разностей между эмпирической и теоретической функцией распределения.

где - накопленная часть

где 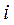- номер образца в вариационном ряду;

- оценка вероятности события ;

- теоретическая (гипотетическая) функция распределения;

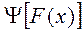- весовая функция.

Обычно весовую функцию используют двух видов:

1.

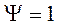
2. 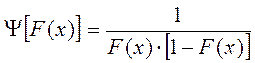- этот вариант весовой функции применяют в тех случаях, когда наибольшее значение имеет соответствие эмпирической функции распределения теоретической в области крайних значений случайной величины (на «хвостах» распределения).

При использовании весовой функции в виде 1 статистику называют статистикой Смирнова, а в виде 2 - статистикой Андерсона-Дарлинга. Критерий применим для любых видов функций F(x), если известны значения их параметров.

Предлагаемая методика прогнозирования выходных характеристик технологической системы на основе обработки статистической информации представлена на рисунке 7.1.

После того, как произведен сбор информации, встает вопрос об ее объеме и тех выводах, которые можно сделать на ее основе. Необходимо отметить, что в ходе сбора информации могут возникать случайные и систематические ошибки. Они должны быть исключены при помощи критериев проверки, иначе выводы, сделанные на основе такой информации не могут быть достоверными.

Собранная на первом этапе информация представляет собой выборку определенного объема. Анализ количества имеющихся данных позволяет сделать вывод о том, расчеты какого уровня возможны.

Далее осуществляется определение выборочных характеристик и затем, если в выборке существуют данные, резко отличающиеся от основной массы, следует проверить, принадлежат ли они выборке или их можно отбросить, так как эти величины являются случайными ошибками.

Для этого применятся различные критерии для отбрасывания резко выделяющихся результатов, используя критерий Ирвина, критерий Груббса или t- критерий

На следующем этапе проводится построение гистограммы, по которой в дальнейшем будет происходить проверка вида закона распределения.

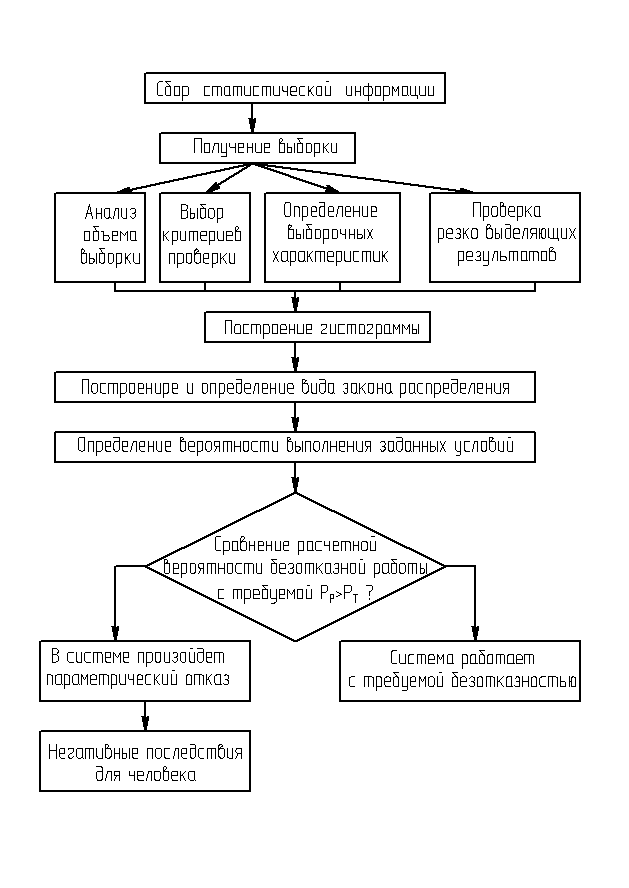
Рисунок 7.1. Алгоритм прогнозирования выходных характеристик системы

Построение гистограммы производится по следующему алгоритму:

1. На первом этапе происходит систематизация исходных данных, то есть производится формирование вариационного ряда .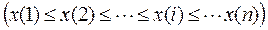

2. Находят размах варьирования по формуле: .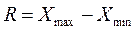

3. Выбирают число интервалов .

4. Находят длину каждого интервала по формуле: .

5. Строят прямоугольную систему координат. По оси абсцисс откладываются все интервалы, на которые разбит вариационный ряд (см. п. 3). Для этого на оси абсцисс проставляют первое значение вариационного ряда, затем к нему нужно прибавить найденную длину каждого интервала и также отметить на оси абсцисс. Повторяют эту операцию столько раз, пока не будут отмечены все интервалы.

6. Высота столбиков гистограммы - это количество значений вариационного ряда, попавших в каждый интервал.

После того как построена гистограмма, можно предположить кривую закона распределения, и соответственно проверить вид самого закона. Если рассматривать статистическую обработку, то этот этап является завершающим, так как имея закон распределения можно исследовать с любых позиций распределение случайной величины.

В нашем случае для расчетов по разработанной методике необходимо определение вероятности попадания исследуемого параметра в заданный интервал или же вероятности непревышения величиной предельно допустимого значения.

На следующем этапе алгоритма производится расчет вероятности безотказной работы или нахождения параметра в заданных пределах. Если мы имеем нормальный закон распределения, то это происходит по формулам и зависимостям, описанным выше. Если же имеет место какой- либо другой закон распределения, то существуют правила нахождения вероятности. К примеру, при логнормальном распределении полученная выборка должна быть сначала переведена в десятичные логарифмы, затем она проверяется на нормальность и, если гипотеза об этом подтверждается, то полученное распределение подчиняется логнормальному закону.

Когда построен закон распределения и определен вид кривой, то параллельно с этим этапом находится максимально (или минимально) допустимое значение исследуемой величины, исходя из условий функционирования системы.

Далее по закону распределения рассчитывается площадь под кривой и, соответственно, вероятность выполнения заданных условий.

На следующем этапе производится сравнение полученной расчетной вероятности с требуемой для данной конкретной системы и данных условий работы.

Если полученное значение больше заданного, то можно утверждать, что в системе не будет параметрического отказа и негативного влияния на технологическое оборудование, человека и окружающую среду.

Если же вероятность безотказной работы меньше требуемого уровня, то в системе с достаточно большой вероятностью произойдет отказ, т.е. выход исследуемого параметра за допустимые пределы, что может привести к серьезным последствиям.

Таким образом, в результате проведения расчетов по предложенной методике можно получить информацию о том, с какой вероятностью исследуемый параметр находится в допустимых пределах или же выходит за них.

Рассмотрим пути решения задачи, когда параметр превышает максимально допустимое значение или находится ниже минимально допустимого и причины, по которым это может произойти (Рисунок 7.2).

В первом случае необходимо проверить, нельзя ли изменить заданный максимум (или минимум). Так как вероятность нахождения изучаемой случайной величины в заданных пределах рассчитывается исходя из закона распределения, то, например, увеличивая значение максимально допустимой величины, можно получить большую вероятность выполнения необходимых условий, чем в предыдущем случае.

Рисунок 7.2.. Условия повторной проверки данных расчета.

Однако изменить предельно допустимое значение практически никогда не представляется возможным, так как это норматив, который не подлежит коррекции.

Следующий вариант заключается в повторной проверке статистической информации, на основе которой был проведен прогноз. Необходимо проанализировать условия сбора информации и возможность наличия систематических ошибок. Если эта гипотеза подтверждается, то производится сбор новой информации для тех же условий работы и расчет повторяется снова.

Если при расчете по каким-либо причинам не были исключены случайные ошибки, то они устраняются и в этом случае сбор новой информации не производится и далее расчет происходит в соответствии с алгоритмом.

Также необходимо отметить случай, когда возможно изменение условий работы системы, это может быть связано с диапазонами изменения температур, режимов нагружения и т.д. Тогда рассматриваемая система может начать функционировать в других условиях, более благоприятных, чем ранее и вредного влияния на другие объекты не произойдет. В этом случае также необходим повторный сбор статистической информации и расчет вероятности безотказной работы.

Четвертый вариант, при котором повторяется цикл расчета, происходит при изменении параметров самой системы. Это могут быть какие-либо конструктивные изменения или изменение величин параметров. В этом случае также необходим повторный сбор статистической информации, так как мы будем иметь дело с уже новой системой с другими параметрами и характеристиками.

Затем для последних двух случаев производится новый расчет вероятности и ее сравнение с нормативом.

Бывает ситуация, когда невозможно изменить ни параметры самой системы, ни условия ее функционирования, а вся информация, на основе которой осуществлялось прогнозирование, верна. При этом вероятность выхода исследуемого параметра за допустимые пределы достаточно высока и не удовлетворяет условиям работы. В этом случае после проведения процедуры прогнозирования необходимо, если, например, речь идет о повышенной концентрации вредных веществ в рабочей зоне, еще до начала работы, поставить дополнительное фильтрационное оборудование, которое будет предотвращать и устранять вредные выбросы.

В каждом случае, когда полученное значение 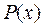не удовлетворяет условиям надежности системы, становится возможным снова повторить предложенную последовательность действий и добиться нужного результата.

Пример выполнения задания № 7

Пусть интервал допустимых норм концентрации задан виде 200 мг/м³ – 300 мг/м³, а выборка:

101; 78; 126,8; 80,1; 21; 107; 36,1; 115; 35,6; 96; 80; 89; 35,8; 126; 12,8; 82; 78,5; 126,3; 100; 78; 115; 24,7; 126; 95; 113; 78,5; 150,3; 82; 36,1; 105; 95; 35,8; 112; 150,3; 82; 109; 35,5; 98; 126,3; 97; 112; 78,8; 126,9; 78,5; 104; 82; 101; 78,8; 126,8; 15,5; 100; 36,1; 103; 96; 89; 80; 101; 13; 98; 80Д; 104; 96; 126; 78; 151; 89; 14,6; 109; 37; 126,8; 82; 150,3; 35,5; 126,9; 96; 35,8; 110; 80; 95; 79; 17,2; 103; 78; 95; 109,8; 101; 35,3; 105; 79,8; 170; 98; 78,6; 126; 82; 100; 36,2; ИЗ; 80,1; 110,4; 36; 105; 78; 95; 108; 104,7; 80; 97; 104.

Вариационный ряд выборки будет:

12,8; 13; 14,6; 15,5; 17,2; 21; 24,7; 35,3; 35,5; 35,5; 35,6; 35,8; 35,8; 35,8; 36; 36,1; 36,1; 36,1; 36,2; 37; 78; 78; 78; 78; 78; 78,5; 78,5; 78,5; 78,6; 78,8; 78,8; 79; 79,8; 80; 80; 80; 80; 80,1; 80,1; 80,1; 82; 82; 82; 82; 82; 82; 89; 89; 89; 95; 95; 95; 95; 95; 96; 96; 96; 96; 97; 97; 98; 98; 98; 100; 100; 100; 101; 101; 101; 101; 103; 103; 104; 104; 104; 104,7; 105; 105; 105; 107; 108; 109; 109; 109,8; 110; 110,4; 112; 112; ИЗ; 113; 115; 115; 126; 126; 126; 126; 126,3; 126,3; 126,8; 126,8; 126,8; 126,9; 126,9; 150,3; 150,3; 150,3; 151; 170.

Как видно , .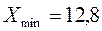

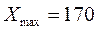Размах варьирования .

Число интервалов 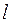положим равным 7 (обычно принимают ).

Длина каждого интервала составляет .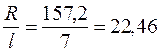

Количество значений вариационного ряда в каждом интервале равно:

Номер интервала:	Количество значений:

Таким образом, имеем следующие границы интервалов:

Номер интервала:	Граница интервалов
	12,8 – 35,26
	35,26 – 57,72
	57,72 – 80,18
	80,18 – 102,64
	102,64 – 125,1
	125,1 – 147,56
	147,56 - 170

Когда необходимые данные найдены, строится гистограмма, представленная на рисунке 2.

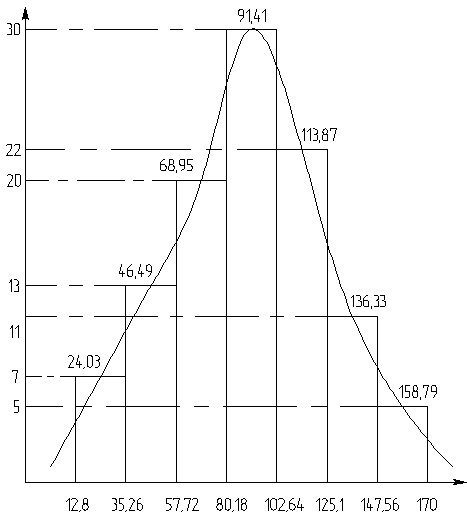
Рисунок 2. Гистограмма выборки.

Определяются середины интервалов как половины от суммы границ интервалов.

Номер интервала:	Значение середины интервала
	24,03
	46,49
	68,95
	91,41
	113,87
	136,33
	1158,79

Найдем среднее значение 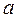, дисперсию 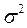среднее квадратическое отклонение :

, , .

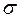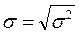Для удобства вычислений составим таблицу

№ интервала	Граница	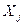середины	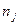число наблюдений
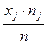
	12,80	35,26	24,03		1,56	282,65
	35,26	57,72	46,49		5,60	227,47
	57,72	80,18	68,95		12,77	80,95
	80,18	102,64	91,41		25,39	0,76
	102,64	125,10	113,87		23,20	119,52
	125,10	147,56	136,33		13,89	222,96
	147,56	170,00	158,78		7,35	222,61

Таким образом, имеем: , .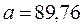

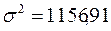Следовательно, 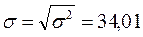и .

Тогда:

левая граница трехсигмового интервала:

,

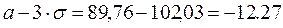правая граница трехсигмового интервала:

.

Как видно, первое и последнее значение вариационного ряда не выходят за рамки трехсигмового интервала, поэтому проверка отбрасывания резковыделяющихся элементов вариационного ряда не требуется.

Дата добавления: 2014-12-26