РЕШЕНИЕ. 4 страница

- действительное значение фактора,

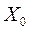- значение фактора на основном уровне,

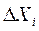- интервал варьирования i-го фактора,

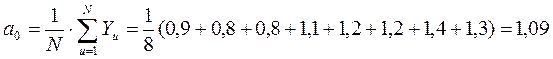
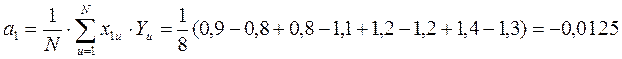
Для определения дисперсии воспроизводимости было дополнительно проведено четыре опыта с факторами на нулевом уровне . Результаты опытов приведены в таблице 8.4 в строках 9 - 12. Как видно для них

.

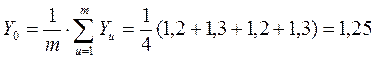Тогда дисперсия воспроизводимости равна:

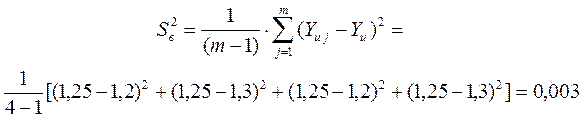
а дисперсия определения параметров линейной модели определится как

.

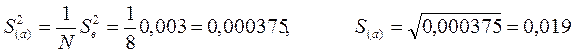Доверительный интервал для параметров линейной модели будет равен:

,

где - значение критерия Стьюдента определено в соответствии с таблицей приложения 6 [2] при принятом уровне значимости 0,05.

Параметр считается значимым, если его абсолютная величина 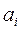больше модуля доверительного интервала : . Как видно, все параметры линейной модели будут значимы.

Нормализованное уравнение линейной регрессии принимает вид:

.

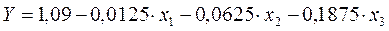Действительное уравнение линейной регрессии в этом случае будет:

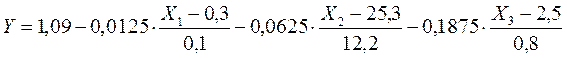
После преобразований:

.

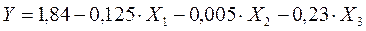Для проверки адекватности полученного уравнения линейной регрессии определяется дисперсии адекватности :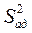

,

где: 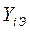- экспериментальное значение параметра шероховатости в i-ом опыте,

- расчетное значение шероховатости по линейному уравнению регрессии для условий i-го опыта,

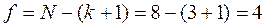- число степеней свободы дисперсии адекватности,

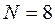- число опытов,

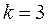- число учитываемых параметров.

Результаты расчета сводятся в таблицу 8.5.

Таблица 8.5 - Результаты расчета адекватности модели линейной регрессии.

Номер опыта	Значения факторов	Экспериментальные значения параметра	Расчетные значения параметра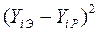
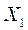
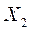
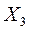
	0,4	37,6		0,9	0,9	0,00
	0,2	37,6		0,8		0,02
	0,4	13,1		0,8	1,0	0,05
	0,2	13,1		1,1	1,1	0,00
	0,4	37,6		1,2	1,1	0,00
	0,2	37,6		1,2	1,2	0,00
	0,4	13,1		1,4	1,3	0,05
	0,2	13,1		1,3	1,3	0,00
Сумма:	0,012

Тогда дисперсия адекватности равна:

.

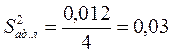Далее определяем расчетное значение функции Фишера 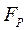рассеивания значений, как отношение дисперсии 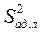адекватности линейного уравнения регрессии и дисперсии воспроизводимости:

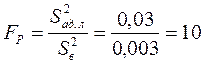
По таблицам распределения значений функции Фишера (таблица приложения 7 [2]) для принятого уровня достоверности 0,95, числа степеней свободы 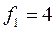дисперсии адекватности и числа степеней свободы 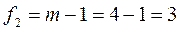дисперсии воспроизводимости, находим критическое значение .

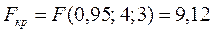Уравнение регрессии считается адекватным, если 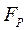< 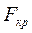. Сравнивая значения 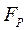и 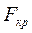, убеждаемся, что 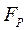> 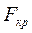, следовательно полученное уравнение регрессии неадекватно.

Переходим к уравнению регрессии вида

,

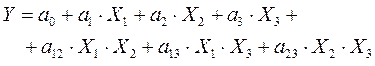учитывающие парные влияния факторов на параметры шероховатости.

Определяем значения коэффициентов парных взаимодействий факторов:

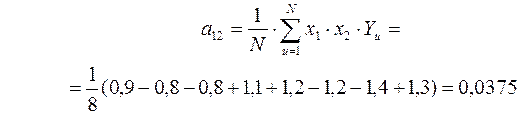
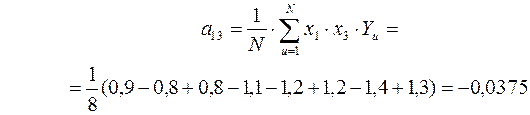
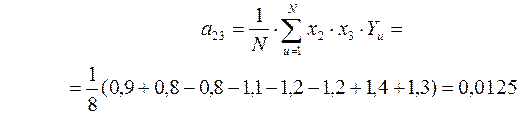
Доверительный интервал для параметров рассматриваемого уравнения регрессии определится как:

Так как значения коэффициентов парных взаимодействий превышают по абсолютной величине доверительный интервал, то следует считать вычисленные параметры значимыми.

Тогда нормализованное уравнение регрессии с учетом парных взаимодействий имеет вид:

Действительное уравнение регрессии с учетом парных взаимодействий будет иметь вид:

После преобразований получаем:

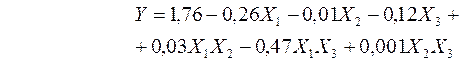
Для проверки адекватности полученного уравнения регрессии с учетом парных взаимодействий определяется дисперсии адекватности :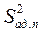

,

где 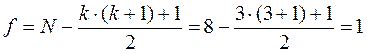- число степеней свободы для уравнения регрессии, учитывающего парные взаимодействия.

Результаты расчета сводятся в таблицу 8.6.

Таблица 8.6 - Результаты расчета адекватности уравнения регрессии

Номер опыта	Значения факторов	Экспериментальные значения параметра	Расчетные значения параметра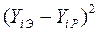
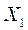
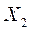
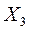
	0,4	37,6		0,9	0,9	0,00
	0,2	37,6		0,8		0,02
	0,4	13,1		0,8	1,0	0,05
	0,2	13,1		1,1	1,1	0,00
	0,4	37,6		1,2	1,1	0,00
	0,2	37,6		1,2	1,2	0,00
	0,4	13,1		1,4	1,3	0,05
	0,2	13,1		1,3	1,3	0,00
Сумма:	0,012

Тогда дисперсия адекватности равна:

.

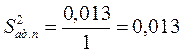Определяем расчетное значение функции Фишера 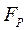рассеивания значений, как отношение дисперсии адекватности и дисперсии воспроизводимости:

По таблицам распределения значений функции Фишера для принятого уровня достоверности 0,95, числа степеней свободы 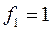дисперсии адекватности и числа степеней свободы 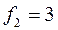дисперсии воспроизводимости, находим критическое значение .

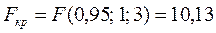Уравнение регрессии считается адекватным, если 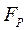< 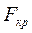. Сравнивая значения 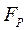и 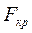, убеждаемся, что 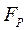> 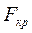, следовательно, полученное уравнение регрессии адекватно и может быть принято.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. С.П. Кудаев. Основы дискретной математики и теории вероятностей. Учебное пособие. Саранск. Изд-во Мордов. ун-та. 2000. – с. 99

2. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистики. Учебное издание. - М.: Изд-во Высшая школа, 2003. – с 404.

3. Е.С. Вентцель, Л.А. Овчаров. Теория вероятностей и ее инженерные приложения. Учебное пособие для студ. втузов. - М.: Издательский центр «Академия», 2003. – 464 с.

4. Пуш Е.А., Синельникова Е.А.. Статистические методы обработки информации в инженерных задачах. Учебное пособие. –М.:ИЦ ГОУ МГТУ «Станкин», 2005 – 80 с.

5. М.М. Кане. Исследование и изобретательство в машиностроении. Практикум.-Мн: УП «Технопринт, 2003.-237 с.

6. Кудаев С.П. Сравнение показателей качества в машиностроении с помощью проверки статистических гипотез. Методическое пособие. Саранск. Изд-во Мордов. ун-та, 1997. – с. 50.

СОДЕРЖАНИЕ

Введение
Задание № 1
Пример выполнения задания № 1
Задание № 2
Пример выполнения задания № 2
Задание № 3
Пример выполнения задания № 3
Задание № 4
Пример выполнения задания № 4
Задание № 5
Пример выполнения задания № 5
Задание № 6
Пример выполнения задания № 6
Задание № 7
Пример выполнения задания № 7
Задание № 8
Пример выполнения задания № 8
Список рекомендуемой литературы

Математическое моделирование процессов в машиностроении: Методические указания и контрольные задания.

Учебно-методическое пособие.

Составитель: Кудаев Сергей Петрович

Редактор Кудаев С.П.

Компьютерная верстка Кудаев С.П.

Лицензия

Подписано в печать

Печать офсетна

Формат

Мордовский государственный университет имени Н.П. Огарева

430027, г. Саранск, ул. Большевистская, 68

Типография «Рузаевский печатник»

Министерства печати и информации РМ

431440, г. Рузаевка, ул. Трынова, 67а

Дата добавления: 2014-12-26