Теоретический материал. Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору

Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Метод конечных разностей — широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на разностные коэффициенты, что позволяет свести решение дифференциального уравнения к решению его разностного аналога, то есть построить его конечно-разностную схему.

Рассмотрим интерполяционную задачу для функции :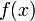

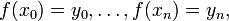
где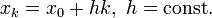

Конечной разностью 1-го порядка называют разность между двумя соседними значениями 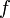в узлах интерполяции, то есть

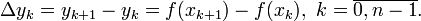
Конечной разностью 2-го порядка называют разность между двумя соседними конечными разностями 1-го порядка, то есть

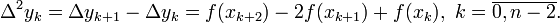
Конечной разностью порядка 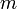(для ) называют разность между двумя соседними конечными разностями порядка 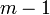, то есть

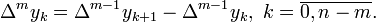
Пример1. Дана таблица некоторой функции

i	xi	yi
	8,8	5,9
	8,9	5,4
		4,8

Вычислить конечную разность Δ²y_0.

Оформим решение в виде таблицы:

i	xi	yi	Δy	Δ^2y
	8,8	5,9	5,4-5,9=-0,5	-0,6-(-0,5)=-0,1
	8,9	5,4	4,8-5,4=-0,6
		4,8

Ответ: Δ²y₀ = -0,1.

Рассмотрим использование интерполянта для нахождения производной функции в точке х по заданной таблично функции у=f(х) методом конечных разностей на примере.

Пример2. Некоторая функция y=f(x) задана в виде таблицы

xi
yi	3,1	5,2	7,2	9,2

Требуется найти значение производной данной функции в некоторой точке. Можно заменить данную функцию, аналитическая запись которой неизвестна, некоторой другой функцией (интерполянтом) y=φ(x), для которой φ(x)⋲f(x) и найти производную функции y=φ(x). Если шаг таблицы h (разность между соседними значениями х) постоянен, то можно воспользоваться формулой:

(*)

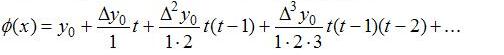Вычисления будем производить с двумя знаками после запятой. Для заданной в виде таблицы функции y=f(x) необходимо найти f '(0,3).

h=1-0=1, t=(x-0)/1=x.

Вычисление конечных разностей оформим в виде таблицы:

i	xi	yi	Δy	Δ^2y	Δ^3y
		3,1	5,2-3,1=2,1	2-2,1=-0,1	0-(-0,1)=0,1
		5,2	7,2-5,2=2	2-2=0
		7,2	9,2-7,2=2
		9,2

Тогда, подставив полученные значения в формулу (*), получим

.

Далее находим φ'(x) и φ'(0,3). Получим, что φ'(0,3)=2,2.

Задание для практической работы по теме «Нахождение значения производной функции в точке Х по заданной таблично функции у=f(х) методом численного дифференцирования».

Некоторая функция y=f(x) задана в виде таблицы. Найти приближенно f ' (a) с помощью конечных разностей..

Вариант 1. а=0,2

xi
yi

Вариант 2. а=2,5

xi
yi

Вариант 3. а=0,2

xi
yi

Вариант 4. а=3,1

xi
yi

Вариант 5. а=0,5

xi
yi

Практическая работа № 17

Тема 4.2: «Приближенное решение задачи Коши дифференциального уравнения y'=f(x,y) с начальным условием y(x₀)=y₀ методом Эйлера».

Цель: Решать приближенно дифференциальное уравнение вида y'=f(x,y) с начальным условием y(x₀)=y₀ (задачи Коши) методом Эйлера.

Теоретический материал :

Численное дифференцирование используется для приближенного вычисления производных функции заданной таблицей и для функций, которые по разным причинам неудобно или невозможно дифференцировать аналитически. В последнем случае вычисляется таблица функции в окрестности исследуемой точки и по этим значениям вычисляется приближенное значение производной.

Рассмотрим численный метод решения дифференциального уравнения первого порядка вида у'=f(x,y), который носит название метода Эйлера.

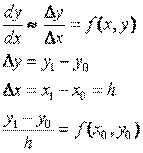
y1=y0+h*f(x0,y0) x1=x0+h	Расчетные формулы для 1-го шага
yi+1=yi+h*f(xi,yi) xi+1=xi+h	Расчетные формулы для i-го шага

Примеры вычислений

Дано у'= xy², x₀=0, y₀ =2, (или по другому y(0)=2), h=0,1. Найти с точностью до десятых y(0,2) (т.е. y₂).

Алгоритм решения поместим для удобства в таблицу.

шаг i	xi	yi	у'= xiyi^2	Δy =h*f(xi,yi)
			0·2^2=0	0,1·0=0
	0+0,1=0,1	2+0=2	0,1·2^2=0,4	0,1·0,4=0,04
	0,1+0,1=0,2	2+0,04=2,04⋲2

Ответ: y(0,2)⋲2

Задание для практической работы по теме «Решить приближенно дифференциальное уравнение вида y'=f(x,y) с начальным условием y(x₀)=y₀ (задачи Коши) методом Эйлера»

Вычислить значение y(0,3) для функции заданного вида с начальными условиями y(0)=2 методом Эйлера.

Вариант 1. у'=y-x²y,

Вариант 2. у'=y+x²y

Вариант 3. у'=(1-2x)·y²

Вариант 4. у'=(1-x²)·y

Вариант 5. у'=(y²-y)·x

Вариант 6. у'=4x-2y

Вариант 7. у'=2x-y

Вариант 8. у'=x+3y

Вариант 9. у'=4x+y

Вариант 10. у'=3x-2y+5

Практическая работа № 18

Тема 4.3: "Приближенное вычисление значения функции y(x) в точке с помощью производной".

Цель: Вычислять приближенное значения функции y(x) в точке с помощью производной.

Теоретический материал :

Вспомним уравнение касательной к графику функции f(x) в точке с абсциссой 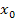. Объяснение по графику и записи рисунка. Каково взаимное расположение точек графика функции и точек касательной вблизи точки касания с абсциссой 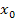? (Ответ: очень близко расположены). Что это означает? Если функция y= f(x) дифференцируема в точке 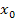, то значения функции в точках из окрестности точки 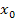очень мало отличаются от значений функции, задающей уравнение касательной, и для всех значений х из окрестности точки 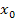можно записать:

f(x)≈ .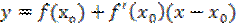

Поскольку 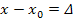x, можно записать

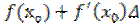f(x)≈ x

Дата добавления: 2014-12-26