Пример вычисления. Пусть дана функция и надо найти её значение при х=2,03

Пусть дана функция 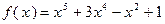и надо найти её значение при х =2,03. Заметим, что при х = 2 легко вычислить f( 2 ) = 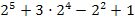= 77.

Применяя выведенную формулу, получим: f(x)=f( 2,03 ),

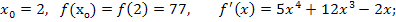
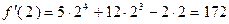, Δ x= х- x₀ = 2,03-2 =0,03;

f( 2,03 )= 77+172·0,03=77+5,16=82,16.

Если произвести вычисления на калькуляторе, то получается f( 2,03 )= 82,297634. Как видим, приближенное значение, полученное при помощи формулы, очень мало отличается от точного значения функции в данной точке.

Задание для практической работы по теме «Приближенное вычисление значения функции y(x) в точке с помощью производной»

Вычислить:

1) приближенное значения функции y(x) с помощью производной;

2) точное значения функции y(x) с помощью ПК или калькулятора;

3) абсолютную и относительную погрешность.

Вариант1: 1,04¹⁵

Вариант2: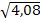

Вариант3: 0,99¹⁵

Вариант4: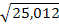

Вариант5: 1,04¹⁰

Вариант6: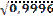

Вариант7: 0,98²⁵

Вариант8: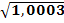

Вариант9: 1,02⁵⁰

Вариант10: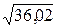

Практическая работа № 19

Тема 4.4: "Вычисление интегралов по формулам прямоугольников".

Цель: Вычислять определенный интеграл приближенно методом прямоугольников.

Теоретический материал :

Введение. Пусть требуется найти определенный интеграл от непрерывной функции ƒ(х). Если можно найти первообразную F(x) функции ƒ(х), то интеграл вычисляется по формуле Ньютона-Лейбница:

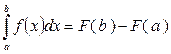
Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция у = ƒ(х) задана графически или табличнo) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.

Рассмотрим две наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников и формулу трапеций, основанные на геометрическом смысле определенного интеграла.

Формула прямоугольников. Пусть на отрезке [а; b], а < b, задана непрерывная функция ƒ(х). Требуется вычислить интеграл, численно равный площади соответствующей криволинейной 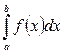трапеции.

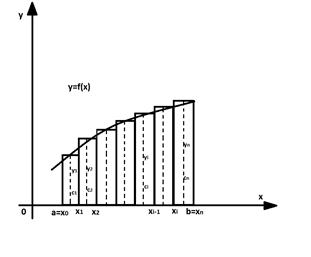
Разобьем основание этой трапеции, т. е. отрезок [а; b], на n равных частей (отрезков) длины 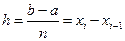(шаг разбиения) с помощью точек х₀= а, x₁, х₂,..., х_n = b. Можно записать, что х_i= х₀+h·i, где i = 1,2,..., n

В середине 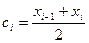каждого такого отрезка построим ординату ŷ_i =ƒ(с_i) графика функции у = ƒ(х). Приняв эту ординату за высоту, построим прямоугольник с площадью h · ŷ_i.

Тогда сумма площадей всех n прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла

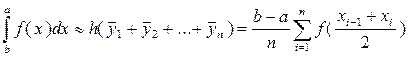
Эта формула называется формулой средних прямоугольников

Дата добавления: 2014-12-26