Пример вычисления

Вычислить методом прямоугольников интеграл 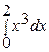, разбив отрезок интегрирования [0; 2] на 4 части.

Решение: Имеем: ƒ(х) = х^3,

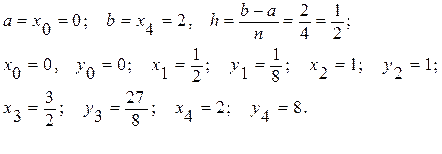
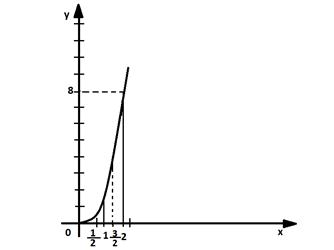
по формуле прямоугольников:

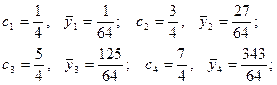
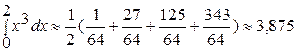
Точное значение интеграла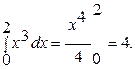

Абсолютная погрешность равна 0,125.

Задание для практической работы по теме «Вычисление интегралов по формулам прямоугольников».

Дан интеграл 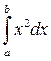. Вычислить:

1). интеграл методом прямоугольников, где a- порядковый № студента по журналу, b=a+2. Разбить отрезок интегрирования на 8 частей.

2). интеграл точно.

3). абсолютную погрешность.

Практическая работа № 20

Тема 4.5: " Вычисление интегралов по формулам трапеций ".

Цель: Вычислять определенный интеграл приближенно методом трапеций.

Теоретический материал :

Формула трапеций. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьем отрезок [а; b] на n равных частей длины 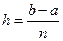Абсциссы точек деления а = х₀, x₁,х₂,...,b = х_n.

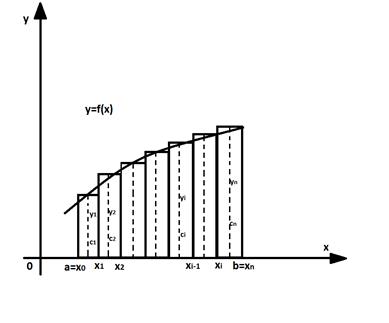
Пусть у₀,у₁...,у_n —соответствующие им ординаты графика функции. Тогда расчетные формулы 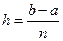для этих значений примут вид х_i = a+h*i, у_i=ƒ(x_i), i= 0,1,2,..., n; Заменим кривую у=ƒ(х) ломаной линией, звенья которой соединяют концы ординат y_i и y_i+1 (i = 0,1,2,...,n). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями у_i, y_i+1 и высотой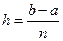

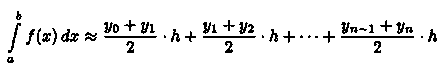
или

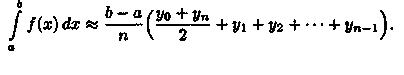
Эта формула называется формулой трапеций.

Пример вычисления.

Вычислить методом трапеций интеграл 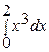, разбив отрезок интегрирования [0; 2] на 4 части.

Решение: Имеем: ƒ(х) = х^3,

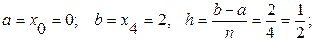
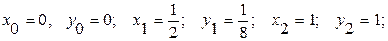
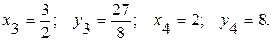
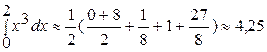
Точное значение интеграла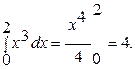

Абсолютная погрешность равна 0,25.

Задание для практической работы по теме «Вычисление определенного интеграла приближенно методом трапеций»

Дан интеграл 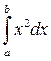. Вычислить:

1). интеграл методом трапеций, где a- порядковый № студента по журналу, b=a+2. Разбить отрезок интегрирования на 8 частей.

2). интеграл точно.

3). абсолютную погрешность.

Список литературы

1. Пехлецкий И.Д. Математика, СПО. – М.: Академия, 2008.

2. Григорьев С.Г., Задулина С.В. Математика, СПО. – М.: Академия, 2009.

3. Валуце И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука,

1980.

4. Подольский В.А., Суходский А.М. Сборник задач по высшей математике. – М.: Высшая школа, 1974.

5. Лисичкин В.Т., Соловейчик И.Л., "Математика", Москва "Просвещение", 2001г.

6. Омельченко, В.П., Курбатова Э.В. "Математика", Москва "Просвещение", 2001г.

7. Пискунов Н. С. Дифференциальное и интегральное исчисление. Т. 2, гл. 13, М., Интеграл-Пресс, 1997

8. Матвеев Н. М. Обыкновенные дифференциальные уравнения. СПб., Специальная литература, 1996

Дата добавления: 2014-12-26