Пример 2.1. Дискретные случайные числа и их имитация

Дискретные случайные числа и их имитация

Ключевые слова: псевдослучайная величина, метод Монте-Карло, эмпирическое дискретное распределение, теоретическое дискретное распределение

При наблюдении и формализации случайных характеристик параметров моделируемой системы необходимо определить их характер. Это необходимо для того, чтобы суметь его воспроизвести (сымитировать) искусственно для экспериментов с моделью. В процессе наблюдения реальной динамики исследуемого объекта у разработчика модели накапливается статистический материал. Он и служит основанием для того, чтобы сделать вывод об особенностях потока. Рассмотрим процесс составления распределения дискретной случайной величины на примере.

Моделируемая ситуация. Частный предприниматель занимается оказанием услуг по доставке багажа по городу (такси). Осуществим построение распределения расхода топлива.

Постановка задачи. При наблюдении за работой такси (20 заказов) был отмечен расход бензина для различных поездок следующим рядом данных: 2,3; 2,1; 4; 2,8; 3,3; 3,5; 2,9; 3,6; 3,9; 3,1; 3,1; 3,1; 4,2; 3,5; 3,6; 2,5; 4,5; 4; 3; 3,7; 3,5 литров. Составьте формулу для среды MS Excel, позволяющую имитировать данное распределение.

Решение. Для начала нужно ответить на вопрос: что будет являться шагом моделирования? Из условия видно, что исследуемый параметр 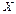измеряется в литрах. Тогда в качестве диапазона моделирования выберем интервал от нуля до пяти: вероятность очень коротких поездок сохраняется, и при этом в ряде данных есть значение, превышающее значение четыре (4,5). В качестве шага моделирования возьмём один литр бензина. Теперь можно подсчитать: сколько значений попадает в каждый интервал (табл. 10, строка 2).

Далее осуществим подсчёт значений, попавших в каждый интервал (строка 3). Так как значения могут быть различны, то нормируем число попадания в интервал к единице (поделим каждое значение строки 3 на число замеров). Гистограмма, построенная по строке 4, называется функцией вероятностей распределения и говорит о том, с какой вероятностью при очередной поездке будет затрачен соответствующий объём бензина (функция вероятностей (А) на рис. 16).

Таблица 10

Плотность появления события

Показатели	Интервалы
0–1	1–2	2–3	3–4	4–5	5–6
Значения	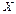–	–	2,3; 2,1; 2,8; 2,9; 2,5; 3	4; 3,3; 3,5; 3,6; 3,9; 3,1; 3,1; 3,1; 3,5; 3,6; 3,7; 3,5	4,2; 4,5	–
Число значений (плотность)
Значения функции вероятностей события X (p (X))			0,3	0,6	0,1
Значения функции вероятностей с накоплением			0,3	0,9

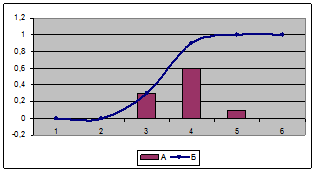
Рис. 16. Функция вероятностей (А) и распределения (Б)
дискретной случайной величины

Вынесем в отдельную строку таблицы (пятая) значения плотности с накоплением. Получим ряд, называющийся функцией распределения: она показывает, какова для выбранного диапазона вероятность появления событий, меньших либо равных 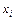(рис. 16 – функция распределения).

Для составления функции, имитирующей полученное распределение в MS Excel, воспользуемся датчиком случайных чисел: запишем в ячейку А1 формулу «=СЛЧИС()». Теперь составим формулу, имитирующую случайную величину, подчиняющуюся данному закону: «=ЕСЛИ(А1>0,9; 4+СЛЧИС(); ЕСЛИ(А1>0,3; 3+СЛЧИС(); 2+СЛЧИС()))». Добавление к каждому сегменту условия слагаемого СЛЧИС() обусловлено тем, что значения моделируемого ряда должны быть дробными.

Вывод: функция вероятностей дискретной случайной величины по расходу бензина представлена на рис. 16. Формула, имитирующая данное распределение, была приведена выше.

Приведённый подход к генерации дискретной случайной величины по таблице или функции распределения называется методом обратной функции.

Для оценки дискретных случайных величин используются некоторые теоретические распределения. Перечислим некоторые из них, отметив их назначение:

• распределение Пуассона – применяется для вычисления вероятности появления случайных событий при заданной интенсивности их появления в единицу времени;

• биномиальное распределение – применяется для вычисления вероятности числа удачных событий из фиксированного объёма серии экспериментов при заданном значении априорной вероятности;

• распределение Бернулли – применяется для вычисления вероятности появления одного исследуемого значения события в одиночной реализации случайного процесса (частный случай биномиального распределения);

• гипергеометрическое распределение – применяется для вычисления вероятности числа меченых элементов в выборке фиксированного объёма из исследуемой совокупности.

Дата добавления: 2014-12-26