Случайные величины и их распределения

Базовые сведения о случайных величинах

Вопросы к главе

þ Какими отличительными признаками обладают пошаговые модели?

þ Каковы основные этапы жизненного цикла пошаговой модели?

þ В чём сущность дискретного модельного времени?

þ Какими параметрами обладает модельное время?

þ Для чего осуществляется предобработка (нормализация) исходных данных?

þ Как получить аналитический вид закономерности, заданный в виде дискретного временного ряда?

þ По каким критериям осуществляется оценка адекватности аппроксимирующей кривой?

þ Как изменяется достоверность данных в результате процесса предобработки?

þ Каков принцип составления законов преобразования информации в пошаговых моделях?

þ Как в программе MS Excel можно реализовать пошаговую модель?

þ Какие процессы можно моделировать при помощи дифференциальных уравнений?

þ Какими отличительными признаками обладают дифференциальные модели?

þ Каковы основные этапы жизненного цикла дифференциальной модели?

þ В чём сущность аналогового модельного времени?

þ Какие типы связей могут быть между подсистемами?

þ Что такое внутренняя динамика объекта?

þ Что такое внешняя динамика объекта?

þ Для чего применяется диаграмма процессов?

þ Каково назначение основных компонентов (блоков) в диаграмме процессов?

þ Каков принцип составления системы дифференциальных уравнений для аналоговых моделей?

þ Как осуществляется переход от диаграммы процессов с системе дифференциальных уравнений?

þ Как в программе MathCAD можно реализовать дифференциальную модель?

Глава 2. ИМИТАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

Ключевые слова: случайность, вероятность, функция распределения, функция плотности распределения, эмпирическое распределение, теоретическое распределение, математическое ожидание, дисперсия, псевдослучайная величина, метод Монте-Карло

Случайность (стохастичность) – одна из тех характеристик реальных процессов, которую необходимо учитывать в процессе их описания. Она может выражаться как во входных факторах модели (случайные значения температуры за окном помещения, высоты волны, номера экзаменационного билета и пр.), так и в особенностях её функционирования (случайные значения времени обслуживания клиента, напряжения в электрической сети, адресов секторов на цифровом носителе при записи файла и пр.). Поэтому при описании исследуемого объекта случайные события и процессы также нужно уметь включать в модель и учитывать при моделировании.

В случае имитации физических, социальных, экономических и прочих явлений с помощью моделирования случайных процессов мы имеем в конечном итоге дело со случайными величинами, которые обладают определенными характеристиками: типом случайной величины (дискретная, непрерывная), законом распределения вероятности (функцией распределения, функцией плотности вероятности). Рассмотрению этих вопросов и будет посвящена вторая глава.

Закономерности случайных колебаний свойств исследуемого объекта (стоимость, время, скорость и пр.) выражаются в оценках параметров законов распределения случайной величины, то есть в виде численных характеристик описываемых событий. Таким образом, по статистическим данным можно оценить вероятность[9] того или иного события или совокупности событий: произойдёт ли то или иное событие и с какой вероятностью.

& Случайная величина (англ. random quantity, random number, variate) – переменная величина, которая в зависимости от случайного исхода испытания принимает некоторое значение из области возможных значений.

Очевидно, что случайным процессом можно назвать такую последовательность проявления свойства моделируемого объекта, при котором его значения являются случайными величинами. Как и модельное время, случайная величина может быть как дискретной, так и непрерывной (аналоговой). Формально это выглядит так:

& Дискретная случайная величина (англ. discrete variate) – это случайная величина, которая может принимать конечное множество возможных значений.

& Непрерывная случайная величина (англ. analog variate) – случайная величина, которая может принимать любое значение из интервала возможных значений.

Так, число бракованных деталей из поставляемой партии деталей будет описываться дискретной случайной величиной, а значение силы тока в электрической сети или отклонение точки падения снаряда от центра цели – аналоговой.

Полная характеристика случайной величины есть закон ее распределения.

& Закон распределения (англ. distribution law) – это соотношение, которое устанавливает связь между значениями случайной величины и вероятностями, соответствующими этим значениям.

Например, множество 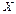возможных состояний конвейера есть , где нормальное функционирование и поломка 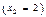описываются функцией вероятности в виде соответствующих вероятносте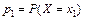й и

Разнообразие представления закона распределения случайной величины составляют ряд распределения, плотность вероятности и функция распределения. Ряд распределения для вышеприведенного примера есть множество точек где

& Функция вероятностей (англ. probability function) – это формальная запись (таблица, график, формула) соотношения возможных значений целочисленной случайной величины 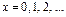и вероятностей соответствующих значений. Обозначается как

& Плотность вероятностей или функция плотности (англ. density function) – это функция, отражающая предел отношения вероятности попадания случайной величины 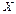в интервал к длине интервала по формуле (6).

(6)

Из данных определений следует, что понятия функция вероятностей и функция плотности эквивалентны, но применимы к различным видам случайных величин: первый относится к дискретным, а второй – к непрерывным. Другой важной характеристикой случайных величин является функция распределения.

& Функция распределения (англ. distribution function) – это функция описывающая вероятность попадания величины показателя 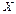в интервал от β до , то есть ставит в соответствие каждому значению вероятность события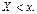

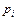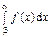Фактически функция распределения рассчитывается одинаково как для дискретной, так и для аналоговой природы случайной величины, то есть является суммой по на или интегралом , где 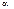– значение оси абсцисс для события В теоретических законах функция распределения может быть симметрична относительно оси ординат, то есть параметр 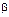будет отрицателен (вплоть до 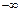). При моделировании большинства физических величин (скорость, вес, число штук и пр.) 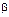приравнивается к нулю.

а	б

Рис. 15. Функции, характеризующие случайные величины:

а – непрерывную, б – дискретную

Графически функция плотности, функция вероятностей и их функции распределения представлены на рис. 15. Видно, что если от функции плотности или от функции вероятностей взять интеграл или сумму соответственно, то он/она будет равняться единице при любых определяющих условиях. Также очевидно, что, зная закон распределения, всегда можно перейти к функции плотности по формуле (6).

Дата добавления: 2014-12-26