Диаграммы процессов и переход к дифференциальным уравнениям

Построение дифференциальных моделей требует от аналитика значительной квалификации в математике и опыта моделирования. Поэтому для упрощения составления дифференциальных уравнений часто применяются промежуточные формы описания моделируемого объекта. Далее будет рассмотрен один из таких методов, получивший название диаграммы процессов языка моделирования DYNAMO.

В 1975 году Джеем Форестером была предпринята попытка моделирования глобальных экологических, социальных и экономических связей. В результате он составил компьютерную модель мировой динамики (рис. 11) и выработал метод схематичного представления взаимодействий объектов модели. Впоследствии такие схемы стали называться диаграммами процессов языка DYNAMO.

Рассмотрим элементы диаграмм процессов.

Таблица 5

Составные элементы диаграммы процессов

Название блока	Обозначение	Параметры	Пояснение
Накопитель			Объект, хранящий величину переменного показателя модели (пересчитывается с каждым шагом моделирования), например величина, показывающая число товара, проданного за день. В накопитель записывается цифра, соответствующая начальному значению моделируемого показателя
Связь			Характеристика направления потока измеряемой величины, например прирост популяции кроликов. Объединяется с блоком «темп»
Генератор		по усло-вию	Внешний неконтролируемый источник, входящий в блок «накопитель», например, источником может являться поток посетителей торговой точки. Это может быть постоянное число (соединяется с блоком «константа») или случайное (внутри контура этого блока записываются параметры распределения)
Константа (коэффициент)			Выявленные или установленные константы, нормы изменения, физические постоянные, например постоянное значение налоговой ставки. Внутри блока записывается число-константа
Преобразователь (функция)			Функция, отражающая характер выявленных зависимостей внутри подсистемы, например закон удвоения прироста населения. Внутри блока через точку с запятой располагаются три параметра: коэффициент возрастания, коэффициент снижения, константа. В случае отсутствия какого-либо из них пишется нуль
Темп			Показатель, характеризующий скорость изменения потока в системе и его характер (положительное или отрицательное воздействие), например скорость снижения спроса на товар при выходе на рынок очередной партии товара-конкурента. Объединяется с блоком «связь»: записывается в виде числа со знаком (+ или -)

Если разделить исследуемый объект на части, то сразу можно будет выделить подсистемы. Каждая подсистема будет накапливать и преобразовывать входной ресурс (параметр), а на выходе перераспределять его по другим подсистемам. Исходя из этого, осуществим классификацию внутренних объектов модели (табл. 5).

В свою очередь, по отношению к отдельным накопителям можно выделить в модели три типа связи:

1) донорский (односторонняя исходящая) – связь, при которой происходит только передача собственного запаса другим (другой) подсистемам;

2) реципиентный (односторонняя входящая) – связь, при которой происходит только принятие запаса от других (другой) частей системы;

3) вольтерровский (двусторонняя)[7] – подсистема и принимает, и отдаёт запас анализируемого параметра.

Рис. 11. Диаграмма процессов модели «Мир-1»

Таким образом, можно осуществлять описание объекта моделирования при помощи сочетания различных объектов. Такое представление и называется диаграммой процесса.

При переходе от диаграммы процессов к формальному описанию модели (системе уравнений), необходимо использовать соответствующие математические механизмы. Для функциональных моделей, где время моделирования является непрерывным, применяются дифференциальные уравнения.

Как было отмечено выше, исследуемый объект (подсистема) представляется на диаграмме процессов в виде блока «накопитель». Он содержит исследуемый параметр x. Тогда линейное уравнение, описывающее внутреннюю динамику объекта в момент времени 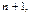будет представлено в виде функции, зависящей от предыдущего значения исследуемой переменной:

, (5)

где – параметр, влияющий на динамику положительно; 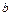– отрицательно, а – константа, которая может иметь как положительное, так и отрицательное значение. Каждая подобная функция может описывать изолированное развитие процесса x, отражая идеальное состояние внутреннего преобразования исследуемой величины без учёта внешних воздействий и влияния других подсистем.

Взаимодействие подсистем модели описывается совокупностью обыкновенных дифференциальных уравнений, каждое из которых включает как внутреннюю динамику развития подсистемы (5), так и воздействие на неё других компонентов модели. Пусть в модели исследуется признак x, имеющийся у m объектов (подсистем). Тогда поведение всей системы описывает система дифференциальных уравнений (4). При этом элемент 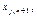где 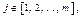для j -го уравнения будет рассчитываться как 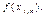Дальнейшие преобразования ведутся по аналогии и представлены в табл. 6. Следует отметить, что данные правила приведены для уравнений первого порядка без степеней.

Например, значения внутри функции (овала) «+1; –1; +12» можно переписать как функцию 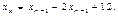Наличие префикса «на единицу товара изменение в» означает умножение предыдущего значения ресурса в накопителе на соответствующий коэффициент. Наличие префиксов «за» или «на» означает прибавление/вычитание константы.

Внешние факторы делятся на управляемые и неуправляемые. Неуправляемым параметром в задаче будет, например, отсутствие сертификата качества международного образца на препарат, изображаемое в виде блока «генератор» и имеющее постоянное значение (блок «константа»). Управляемые (локальные) взаимодействия описываются стрелками) с блоками типа «темп», в которых пишется значение параметра взаимодействия единицы одного ресурса (накопителя) на значение другого. Стрелки рисуются так, чтобы отражать направление воздействия с учётом знака (положительное или отрицательное). Если известно, что каждая особь вида a отрицательно воздействует на численность 5 особей вида b за единицу времени (шаг моделирования), то в уравнение второго вида будет записано слагаемое Подробнее эти принципы будут проиллюстрированы далее на примерах.

Таблица 6

Соотношение элементов условия задачи, блоков диаграммы процессов и элементов дифференциальных уравнений

Блоки диаграммы процессов	Элемент дифференциального уравнения	Типовые формулировки описания в задачах	Пояснение
	Критерий исследования для каждой подсистемы	• m предприятий производят… • m тел в вакууме воздействуют друг на друга гравитационным полем… • Известно, что целевая группа потребителей делится на m категорий…	Система состоит из m уравнений. Каждое пересчитывается с наступлением нового шага моделирования
	Знак влияния темпа (+ или –) в системе уравнений	• Каждая особь волка убивает за сезон… • Отрицательная реакция спроса на единицу товара…	Указывает на то, какой объект модели воздействует на j -е уравнение в системе
	Функция, независящая от	• Таможенная пошлина составила… • Чистота вещества в катализаторе ускорила химическую реакцию в… • Влияние колебания цен на бензин отрицательно сказалось на …	Внешнее воздействие на систему. Вводится через соединение с константой или законом распределения
	Константа в системе уравнений	• Показатели прибора дали погрешность расчётов… • Государственная пошлина равна…	Постоянные величины, действующие на подсистему из внешней среды
	Функция внутренней динамики f (xn), описываемая отдельно от системы	• Внутриатомные связи приводят к… • Внутренняя динамика описывается… • Технологический цикл состоит из…	Внутренняя динамика развития, имеющая три параметра, записывающихся через «;»
	Конструкция xixjc в системе уравнений	• Конкурирующая фирма снижает спрос на товар с коэффициентом c … • Положительная реакция препарата на один литр биомассы со скоростью c …	Величина, отражающая степень влияния подсистемы xi на подсистему xj с коэффициентом c

Используя табл. 6, можно реализовать переход от содержательного изложения условий к уравнениям. Имея же формализованную модель, не составит труда реализовать её в любой системе математических расчетов (MathCAD, MatLab, Maple, Mathematica, пр.).

Дата добавления: 2014-12-26