Сущность дифференциального (функционального) подхода

Построение аналоговой (дифференциальной) аналитической модели

Ключевые слова: аналоговая (дифференциальная, функциональная) модель, дифференциальное уравнение, система уравнений, диаграмма процессов, связи между подсистемами

Моделирование, основанное на использовании аналоговых законов, немного отличается от работы с дискретными данными. Так как природа аналоговых величин не имеет чётких переходов между своими состояниями, то и их просчёт может производиться в любой точке из области определения модельного времени. Этого можно достичь, когда форма представления закономерностей имеет вид формул, а точнее – обыкновенных дифференциальных уравнений. Поэтому данный тип моделей получил название дифференциальных или функциональных математических моделей.

Дифференциальные уравнения как инструмент описания процессов в механике впервые стали использоваться с XVII века. В моделировании они широко применяются для описания траектории движения объектов, изменения численности биологических популяций, просчёта экономических показателей и пр.

& Дифференциальное уравнение (англ. differential equation) – уравнение для определения функции, связывающее переменные, искомые функции и их дифференциалы или производные.

Отличие дифференциальных уравнений от других математических конструкций заключается в том, что на каждом этапе просчёта исследуемого процесса они содержат ссылки на его предыдущие состояния. Существует много различных видов дифференциальных уравнений, и все они используются для описания различных процессов и явлений. Наиболее простые процессы поддаются описанию обыкновенными дифференциальными уравнениями, каноническое определение которых следующее:

& Обыкновенное дифференциальное уравнение (англ. ordinary differential equation) – уравнение, в кото­ром неизвестной является функция от одной независимой переменной, причём в это уравнение входит не только сама неизвестная функция, но и её производные различных порядков.

Обыкновенные дифференциальные уравнения – один из самых распространённых инструментов исследования детерминированных сложных систем. Они используются тогда, когда с достаточной точностью можно описать как внутренние механизмы динамики отдельных подсистем, так и их влияние друг на друга.

Сущность моделирования обыкновенными дифференциальными уравнениями заключается в том, что для расчета очередного значения исследуемого показателя нужно знать только его предыдущее значение и характер преобразования:

(2)

Задав начальные условия просчёта, то есть 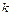и можно всегда проследить дальнейшее поведение модели:

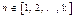, . (3)

Графически такую схему можно представить как процесс с обратной связью (рис. 10), где 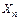– значение переменной в момент модельного времени а – система внешних воздействий (помехи и управление).

Рис. 10. Процесс с обратной связью

Если требуется описать взаимодействие нескольких объектов (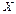 в (3) является вектором), то для каждого составляют отдельное уравнение, а потом их объединяют в систему:

(4)

Особенностью такого подхода является то, что описание моделируемого объекта строится относительно одного показателя (прибыли, концентрации вещества, объёмов производства, скорости движения и пр.), по которому идёт итеративный просчёт. Даже если необходимо исследовать взаимодействие обособленных подсистем, достаточно выявить зависимость каждого из них от исследуемого параметра и описать взаимодействия в виде системы дифференциальных уравнений.

Дифференциальное моделирование обладает следующими признаками:

– аналоговым временем моделирования;

– взаимовлияющими законами динамики моделируемых подсистем, просчитываемыми одновременно (как система уравнений);

– однородными показателями в рамках одной модели;

– детерминированными законами развития каждой подсистемы.

Очевидно, что выявление корректных аналитических законов динамики подсистем и их объединение в рамках одной модели – процесс довольно сложный и требующий при просчёте значительных вычислительных мощностей.

Дата добавления: 2014-12-26