Пример 1.3

Примеры

Общие замечания. Дифференциальные модели наиболее естественно рассматривать в математических пакетах. Для примера выберем среду MathCAD.

Моделируемая ситуация. Фармацевтическая компания производит два вида новых сверхэффективных лекарственных препаратов от психических расстройств: препарат А и препарат Б. Данные препараты различаются по продолжительности фармакологического действия и цене. Фармакологическое действие препарата А короче, а его производство значительно дешевле, чем препарата Б. На рынках сбыта конкурентов у этой продукции пока нет. Требуется оценить спрос на товар для планирования объёмов производства, если известны некоторые данные по динамике покупок после продажи первых партий.

Постановка задачи. После исследования рыночной ситуации и динамики продаж стало известно, что за неделю на одну проданную партию препарата А приходится повышение спроса в 3,8 раз. При этом снижение спроса за счёт побочных эффектов на одну партию товара имеет коэффициент 0,007, а долгосрочный заказ на экспорт обеспечивает дополнительный спрос на 4,32 партии в неделю.

На препарат Б происходит постоянное повышение спроса на 2,7 партии в неделю. За счёт наличия побочных эффектов при приёме препарата наблюдается снижение спроса с коэффициентом 0,45.

На спрос влияет и взаимная рыночная конкуренция товаров. Для препарата А:

– снижение спроса от конкуренции с более эффективным продуктом Б на единицу товара – 0,003 партии;

– отсутствие сертификата качества международного образца снижает спрос с постоянной скоростью 0,2 партии за неделю.

Для препарата Б:

– повышение спроса от конкуренции с более дешевым и опасным препаратом А на единицу товара – 0,029 партии;

– отрицательный эффект от появления на рынке подделок (контрафакта) уменьшает спрос на 1,8 партии еженедельно.

Осуществите моделирование на следующие 60 недель, если известно, что начальный спрос на препарат А – 12 партий в неделю, на препарат Б – 7. Предложите недельную норму производства препаратов.

Решение. Для начала выявим параметр исследования в модели – это объём спроса на продукцию. Следовательно, моделироваться будет покупательская активность на каждый из двух видов товара, представленных в виде отдельных подсистем.

Составим диаграмму процессов. Из условия видно, что все факторы можно разделить на внутренние (внутрипроизводственные) и внешние (рыночная среда). Они описаны отдельно в первой и второй части условия соответственно. Будем рассматривать их параллельно с составлением диаграммы процессов. Так как выделены две подсистемы, то диаграмма будет иметь два блока типа «накопитель» (прямоугольник на рис. 12) с вписанными в них начальными значениями.

Рис. 12. Диаграмма процессов к задаче об объёме продаж препаратов

Внутрипроизводственные факторы выносятся в блок «преобразователь»: сначала записывается цифра при положительном множителе значения накопителя, затем – при отрицательном, а потом – константа. Знаки для каждой цифры определяются по условию. Так, для товара Б отрицательным коэффициентом внутренней динамики спроса является значение –0,45, а константой – значение 2,7, положительный множитель отсутствует. Следовательно, в блок «функция» войдут цифры «0; –0,45; 2,7».

Внешняя динамика для препарата А будет складываться из внутренней динамики (соединение блоков «накопитель» и «функция»), воздействия неконтролируемой оценки медицинского сообщества (константа –0,2) и конкурирующего воздействия препарата Б (связь от накопителя Б с значением в блоке «темп» –0,003). Следует подчеркнуть, что все внешние воздействия на накопитель (исключая блок «функция») имеют стрелки (связи), направленные в его сторону.

Опираясь на данные из диаграммы процессов, осуществим формализацию модели. Для начала опишем внутреннюю динамику спроса на препараты А и Б:

,

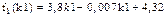Взаимодействие подсистем модели и описание влияния внешних факторов представляется другой конструкцией – системой дифференциальных уравнений. Для каждого накопителя существует своё уравнение, включающее как внешнюю, так и внутреннюю динамику изменения исследуемой величины вида. Если спрос на первый препарат обозначить через 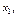а на второй – через 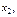то дифференциальное уравнение для первого накопителя будет выглядеть так: Второе уравнение составляется аналогичным образом.

Особенность дифференциальных моделей заключается в том, что, в отличие от пошаговых, где пересчёт величин идёт изолированно друг от друга, каждое уравнение зависит ещё и от других объектов системы. Поэтому рассматриваются не отдельные значения каждого накопителя, а возможность их совместного существования во времени, так называемая коэволюция. Для этого оба уравнения объединяются в систему в соответствии с формулой (4).

Осуществим перевод формальной записи модели в виде команд для среды моделирования (в данном случае MathCAD). Запись и решение системы линейных дифференциальных уравнений в этом математическом пакете чрезвычайно просты. Для этого необходимо объявить правила индексации (оператор ORIGIN), затем задать коэффициенты уравнений, описать функции внутренней динамики, составить и решить систему дифференциальных уравнений. На рис. 13 представлена последовательность команд, реализующих моделирование.

Здесь система уравнений 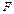зависит от значений исследуемой величины (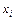) и времени (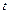), измеряемом в неделях. Начальные условия задаются в системе непосредственно перед просчётом модели. Процесс моделирования осуществляется с помощью функции rkfixed, имеющей пять обязательных параметров:

– переменную, по которой осуществляется дифференцирование (x);

– начальный момент моделирования (0);

– конечный момент моделирования (60);

– число точек между начальным и конечным моментами моделирования (2000, задаётся условно);

– матрицу, содержащую систему дифференциальных уравнений (в примере F).

Рис. 13. Листинг модели в окне программы MathCAD

Проведём анализ результатов моделирования. Переменная X содержит результаты 61 эксперимента, показывая поведение каждой подсистемы. На рис. 14 представлена динамика спроса на рассматриваемые медицинские препараты А и Б. Первая размерность переменной X содержит шаг моделирования, а другие – значения спроса.

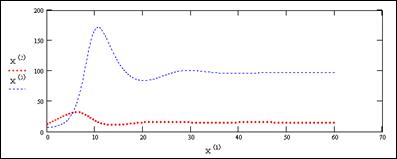
Рис. 14. Динамика спроса на конкурирующие товары

Несмотря на то, что товары конкурируют на рынке сбыта, со временем спрос на них стабилизируется. Этому способствует отрицательная петля взаимного усиления спроса, влияющего на продажу препаратов. Произведя ряд экспериментов, можно увидеть, что, изменяя начальное количество партий, мы получили проявление той же закономерности, имеющей стационарное состояние. Такая динамика говорит о наличии устойчивых целевых групп потребителей.

Выводы. На основе получившейся динамики спроса можно дать заключение, что в неделю рационально осуществлять производство 97 партий препарата А и 15 партий препарата Б. Нелинейное поведение начального этапа отражает особенности конкурентной борьбы товаров на рынке. Взаимное влияние препаратов изначально имеет «взрывной» характер, но к 37 неделе стабилизируется вокруг постоянных значений.

Дата добавления: 2014-12-26