Непрерывные случайные числа и их имитация

Ключевые слова: псевдослучайная величина, метод Монте-Карло, теоретический закон непрерывной случайной величины, равномерное распределение, нормальное распределение, показательное распределение

Имитирование случайного дискретного процесса, имеющего сложное распределение, – трудоёмкий процесс. Поэтому эмпирическое распределение зачастую аппроксимируют с помощью стандартных теоретических распределений. Это позволяет сделать процесс генерации случайных событий намного проще и управляемей. Рассмотрим наиболее часто применяемые теоретические распределения.

Равномерное распределение – распределение случайной величины, принимающее любое значение из своей области определения с равной долей вероятности. Пример равномерного распределения представлен на рис. 17.

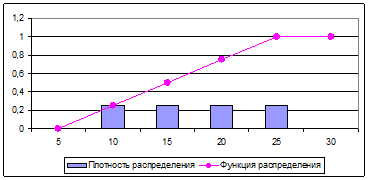
Рис. 17. Равномерное распределение для 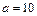и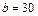

Область распределения характеризуется двумя числами – минимальным (a) и максимальным (b) значениями, между которыми и будет находиться случайная величина. Для данной области распределения функция плотности имеет вид:

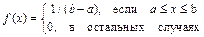. (10)

Чтобы получить ряд чисел, подчинённых равномерному закону распределения, недостаточно формулы (10). Пусть дано случайное число n из интервала от 0 до 1. Тогда его можно преобразовать к равномерному распределению на интервале 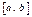по следующей формуле:

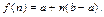(11)

Область применения – любые процессы, не имеющие закономерности поведения, то есть демонстрирующие равную возможность появления любого значения на исследуемом диапазоне.

Распределение Гаусса (нормальное) – распределение случайной величины, плотность вероятности значений которой подчиняется следующему закону:

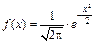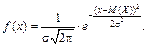или (11)

Гауссово распределение имеет два параметра: матожидание и среднеквадратичное отклонение (рис. 18). Первый вариант формулы (11) используется для генерации нормально распределённых чисел с матожиданием 0 и отклонением 1 (нормированное распределение), второй вариант позволяет задавать собственные значения параметров распределения (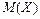 задаёт смещение по оси абсцисс, а σ – крутизну и островершинность).

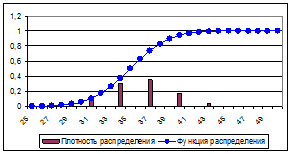
Рис. 18. Гауссово распределение для 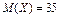и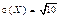

Для получения числа, распределённого по нормальному закону, требуется осуществить преобразование:

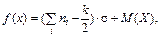
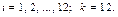(12)

Область применения – ситуации, где исследуемая величина имеет случайный характер, но её значения симметрично колеблются вокруг одного значения с определённым разбросом.

Показательное (экспоненциальное) распределение – распределение случайной величины, плотность вероятности значений которой подчиняется следующему закону:

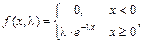
где 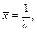а Экспоненциальное распределение имеет один параметр 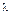, а параметры, рассчитываемые по формулам (7) и (9), совпадают (рис. 19).

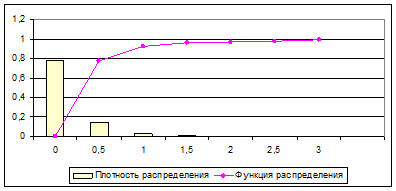
Рис. 19. Показательное распределение для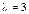

Для получения числа, распределённого по экспоненциальному закону, требуется осуществить преобразование:

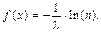
Область применения – ситуации, где исследуемая величина имеет случайный характер, но её значение колеблется вокруг одного значения с определённым разбросом.

Гамма-распределение – распределение случайной величины, плотность вероятности значений которой подчиняется следующему закону:

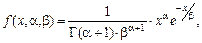
где 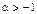, а 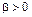, оператор 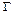– гамильтониан. Параметр 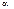определяет эксцесс, а 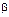– островершинность, которая играет роль шкалы (рис. 20). Если значение параметра 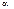– целое положительное число, то такое распределение ещё называют распределением Эрланга. Нормальное распределение и показательное распределение являются частным случаем гамма-распределения.

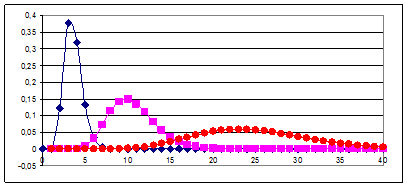Рис. 20. Три различных варианта функции плотности гамма-распределения ( = 12; 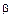= 0.3, 0.8 и 0.2 соответственно)

Область применения – ситуации, где исследуемая величина имеет случайный характер, но её значения неравномерно колеблются вокруг одного значения с определённым разбросом.

Кроме этих теоретических распределений, на практике также часто применяются распределение Пирсона (хи-квадрат), распределение Стьюдента и распределение Фишера, отражающие специфику значений формул (7), (8) и (9).

Рассмотрим генерацию непрерывных случайных величин на примере, реализованном в MS Excel.

Дата добавления: 2014-12-26