Векторний спосіб задання руху точки

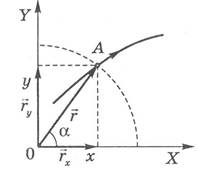Точка задана радіус-вектором, якщо відомі його довжина (числове значення) і напрям у просторі, тобто значення його проекцій r_x, r_y, r_z на осі координат ОХ, ОУ, OZ, або величини кутів між радіус-вектором і осями координат. Для випадку руху на площині (рис. 1.4) маємо:

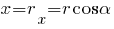
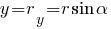
Тут — модуль вектора overline{r}, r_x та г_у — його проекції на осі координат. Усі три величини — скалярні; одночасно х та у — координати точки А.

Вектор г можна розкласти на складові вздовж координатних осей X та У, тобто записати як суму двох векторів:

Три останні рівняння встановлюють зв’язок між координатним і векторним способами означення положення точки.

Векторний спосіб опису руху точки визначає залежність радіус-вектора від часу:

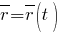
Дане являє собою рівняння руху точки, записане у векторній формі. Якщо воно відоме, то для будь-якого моменту часу можна розрахувати радіус-вектор точки, тобто визначити її положення так само, як і координатним способом. Таким чином, задання трьох скалярних рівнянь відповідає заданню одного векторного рівняння.

Природній спосіб задання руху точки Застосовується коли координата точки заздалегідь відома, тоді положення точки в просторі визначальних 4-х елементів (мал.10.6):. Просторів. Крива. Дугова координата С на кривій 3. Початок відліку дугової координати. Напрямок позитивного відліку дугової координати При русі т. М дугова координата С змінюється із часом: S=S(t) (10.11)

Залежність 10.11 - кінематичне рівнянням руху або законом руху точки М по заданій траєкторії. Функція S(t) –передбачається неприривною, однозначної й двічі диференційованою. Позначимо - довжина шляху, що пройшла точка, яка рухається. Шлях точки - відстань, що пройшла точка уздовж траєкторії в напрямку руху точки. Нехай задані рівняння 10.3. З курсу диференціальної геометрії елемент дуги траєкторії ds виписується виразом:

2 Швидкість руху. Середня шляхова швидкість, середній вектор швидкості, миттєва швидкість. Геометричний зміст похідної..Визначення миттєвої швидкості при різних способах(векторному, координатному, «природному») опис руху. Знаходженя положенняматеріальної точки за відомою залежністю миттевої швидкості від часу та початковими умовами. Знаходження шляху пройденою матеріальною точкою за певний проміжок часу., геомеметричнгий зміст визначеного інтегралу. Знаходження середніх значень скалярних і векторних функцій.

Шви́дкість — фізична величина, що відповідає відношенню переміщення тіла до проміжку часу, за який це переміщення відбувалось. Швидкість — величина векторна, тобто вона має абсолютну величину і напрямок. У системі СІ швидкість вимірюється — м/с

.

Середньою швидкістю нерівномірного руху ц, за даний відрізок часу І називають фізичну величину, що дорівнює відношенню переміщення до відрізка часу, за який це переміщення відбулося:

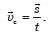
Миттєва швидкість тіла — це його середня швидкість за такий малий відрізок часу, який включає цей момент, що протягом цього відрізка рух тіла можна вважати рівномірним.

Похідною функції f(x) у точці х₀ називається границя (якщо вона існує) відношення приросту функції у точці х₀ до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x₀).

Похідна функції має такий геометричний зміст: похідна функції в заданій точці є кутовим коефіцієнтом дотичної до графіка функції в цій точці, тобто дорівнює тангенсу кута нахилу дотичної до графіка функції в заданій точці

Дата добавления: 2014-12-26