Простая регрессия

В ходе простой регрессии можно получить следующие результаты:

- выбрать из нескольких математических моделей ту, которая с большей точностью описывает экспериментальную зависимость (по максимуму коэффициента корреляции, по минимуму стандартной ошибки, по минимуму значимости и т.п.);

- построить прогноз на будущее на основе выбранной модели с 95-процентным доверительным интервалом;

- провести анализ регрессионных остатков.

Процедура простой регрессии для экспериментальных зависимостей от одной переменной и временных рядов предоставляет возможность строить наиболее употребительные регрессионные модели.

Так, например, для описания неограниченных и монотонно-возрастающих или монотонно-убывающих экспериментальных зависимостей могут быть использованы следующие модели:

- линейная модель 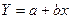применима для зависимостей, у которых первая производная (скорость изменения Y, прирост Y) постоянна.

- параболическая модель 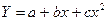характеризуется тем, что ее первая производная изменяется по линейному закону.

- логарифмическая зависимость 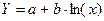применима для моделирования медленно изменяющихся процессов, поскольку ее первая производная убывает обратно пропорционально Х.

- экспонента 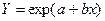применима для зависимостей, у которых логарифмы Y изменяются по линейному закону.

Скорость роста степенной функции 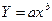при больших Х больше логарифмической и меньше экспоненциальной, а также может быть меньше или больше, в зависимости от своих параметров, скорости роста линейной функции.

Для описания ограниченных монотонно-возрастающих и монотонно-убывающих экспериментальных зависимостей (зависимостей с насыщением, значения которых стремятся к некоторому пределу) могут быть применены следующие модели:

- при предельном значении 0: степенная модель 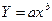, экспонента 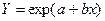, , 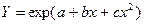гипербола ;

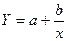- при произвольном предельном значении: модифицированные степенная функция 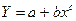, экспонента и гипербола ;

- в случае двух пределов: логистическая модель , в которой значение параметра " а " определяет нижний предел, а значение параметра " b " - расстояние между нижним и верхним пределами.

Для моделирования зависимостей с одним максимумом (минимумом) применимы парабола 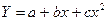(неограниченная зависимость), экспоненциально-параболическая модель 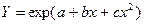(колоколобразная симметричная зависимость с максимумом в Х=0 и пределом Y=0) и функция оптимума 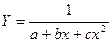, 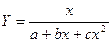(зависимость с резким экстремумом и последующим пологим приближением к пределу Y=0).

Для представления зависимостей с несколькими экстремумами применимы полиномиальные модели , степень которых минус единица определяет число экстремумов.

Для описания периодических зависимостей (зависимостей с незатухающими колебаниями) применима модель с синусоидой , в которой параметр " b " определяет долговременный прирост, параметр " c " - амплитуду колебаний, а параметр " e " - длину периода колебаний.

Перед выбором модели для получения представления о характере зависимости Y от X целесообразно построить функциональный график исходных данных. Часто бывает целесообразно рассчитать несколько моделей и среди тех, для которых может быть принята гипотеза адекватности экспериментальным данным, произвести выбор по критерию минимума стандартной ошибки.

Следует также учитывать, что ряд нелинейных моделей в процессе вычислений приводятся к линейной модели с предварительным преобразованием значений переменной–отклика Y, что влечет минимизацию не самих отклонений экспериментальных точек от регрессионной кривой, а взвешенных этим преобразованием отклонений. Если такой эффект нежелателен, можно воспользоваться моделью по вводимой формуле, вычисление которой не содержит предварительного преобразования.

Дата добавления: 2014-12-26