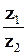Множення та ділення комплексних чисел

Тригонометрична форма комплексного числа

Користуючись формулами (1.13), можна будь-яке комплексне число, що відмінне від нуля, представити в тригонометричній формі:

z = x + yi = r cos j + i r sin j = r (cos j + i sin j). (1.23)

Таким чином, остаточно маємо:

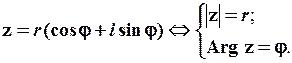(1.24)

Якщо j таке, що – p < j ≤ p, то j = arg z.

ü Тригонометрична форма (1.24) комплексного числа має такі особливості:

· множник перед дужками як радіус обов’язково додатне число (r > 0);

· алгебраїчне значення аргументу j однакове за величиною та знаками для синусу і косинусу;

· доданки cos j та sin j записуються зі знаком плюс, хоча можуть бути додатні або від’ємні в залежності від значення j.

ü Тригонометрична форма комплексного числа зручна для здійснення множення та ділення комплексних чисел, піднесення до степеня n та добування кореня степеня n комплексного числа.

Здійснимо множення двох комплексних чисел, що задані в тригонометричній формі, як множення двох многочленів:

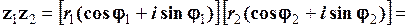
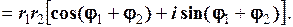
Отже,

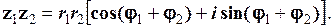(1.25)

Або

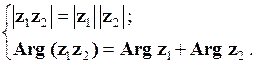(1.26)

ü Модуль добутку комплексних чисел дорівнює добутку їх модулів, а аргумент – сумі їх аргументів (рис. 1.6, а).

ü Здійснивши аналогічним чином ділення комплексного числа 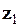на комплексне число за умов що ≠ 0, одержимо:

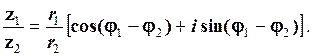(1.27)

Тобто

(1.28)

ü Модуль частки від ділення комплексного числа 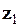на комплексне число дорівнює частці їх модулів, а аргумент – різниці аргументів діленого і дільника (рис. 1.6, b).

		b)

z₁

z = z₁z₂

z₂

z =

z₂

z₁

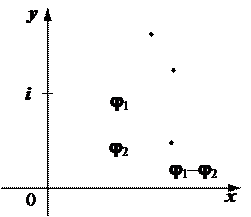Рис. 1.6. Множення та ділення комплексних чисел

Рис. 1.5

ü Тригонометрична форма дозволяє досить легко здійснювати множення та ділення чисел.

ü Так як , то множення числа z на і зводиться до повороту вектора z на кут π/2 проти годинникової стрілки, а ділення z на і зводиться до повороту вектора z на кут π/2 за годинниковою стрілкою.

Дата добавления: 2014-12-23