Контрольні запитання

Розв’язування.

Розв’язування.

Розв’язування.

Приклади розв’язування індивідуальних задач

Задача 1.1.

1. Задане в алгебраїчній формі число 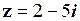записати в тригонометричній та показниковій формах.

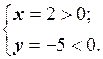
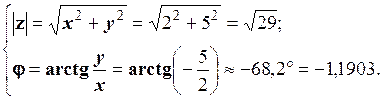
В тригонометричній формі:

В показниковій формі: .

2. Задане в алгебраїчній формі число 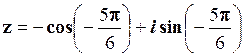записати в тригонометричній та показниковій формах.

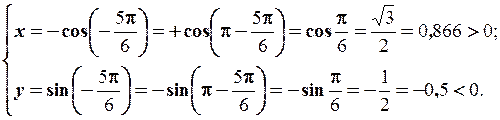
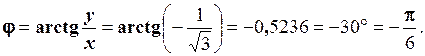
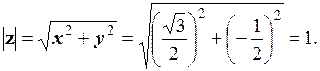
В тригонометричній формі:

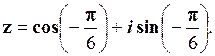
В показниковій формі: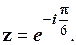

Задача 1.2. Спростити вираз 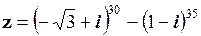до числа в алгебраїчній формі.

1. ; .

.

.

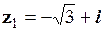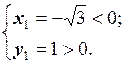
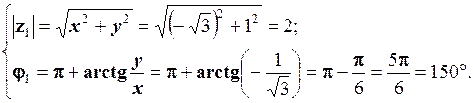
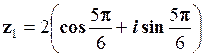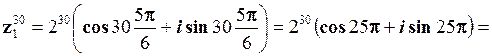
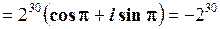2. .

.

.

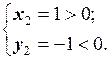
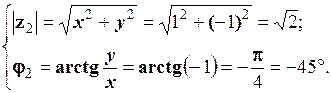
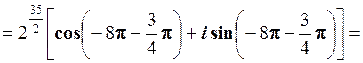
3. .

.

.

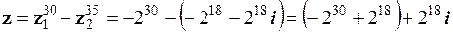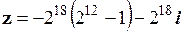Задача 1.3. Знайти корені .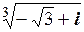

Розв’язування. Так як n = 3, то одержимо три корені.

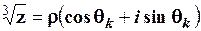; , k = 0, 1, 2.

1.

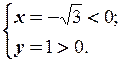
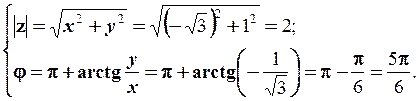
Отже,

.

2. .

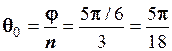3. .

4. 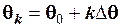, k = 0, 1, 2.

.

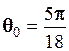. Отже, .

. Отже, .

Значення 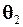зменшуємо на 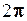. Тоді

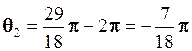. Отже, .

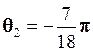5. .

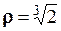Отже,

6. ;

;

.

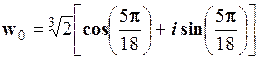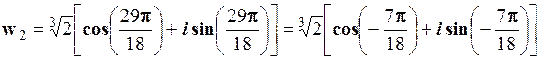Зобразимо всі три корні на колі радіуса .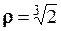

1. Уявна одиниця та її властивість.

2. Алгебраїчна форма комплексного числа, його модуль, реальна та уявна частини.

3. Додавання та множення комплексного чисел в алгебраїчній формі.

4. Віднімання та ділення комплексних чисел в алгебраїчній формі.

5. Геометрична форма комплексного числа, полярні координати.

6. Перехід від декартових координат до полярних.

7. Аргумент числа z та його головне значення.

8. Формула визначення через значення .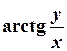

9. Додавання та віднімання векторів, що зображують комплексне число.

10. Тригонометрична форма комплексного числа та її особливості.

11. Множення та ділення комплексних чисел в тригонометричній формі.

12. Формула Муавра.

13. Добування кореня степеня n, основні формули.

14. Алгоритм добування кореня степеня n.

15. Яке число коренів має вираз ?

16. Формула Ейлера.

17. Показникова форма комплексного числа.

18. Множення та ділення комплексних чисел в показниковій формі.

19. Спряжені комплексні числа, їх модулі, сума та добуток.

20. Довести, що .

21. Які дії над комплексними числами зручно здійснювати, якщо вони задані в алгебраїчній, тригонометричній та показниковій степенях.

22. Що одержують при діленні та множенні числа z на уявну одиницю i.

23. Скільки значень має вираз для цілих дійсних n та n = 0.

24. Формула та характерні точки одиничного кола на комплексній площині.

Дата добавления: 2014-12-23