Приклади. Приклад 1.1. Визначити число , де n– ціле дійсне число або нуль

Приклад 1.1. Визначити число 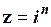, де n – ціле дійсне число або нуль.

Розв’язування. Спочатку розглянемо додатні значення n. Будемо послідовно множити число і начисло і:

n = 1: ;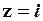

n = 2: 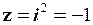(по визначенню);

n = 3: ;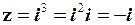

n = 3: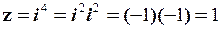

і так далі.

Результати послідовного множення на число і показані на рис. 1.11, а.

При множенні числа на уявну одиницю і число z треба повернути на кут по одиничному колу за годинниковою стрілкою.

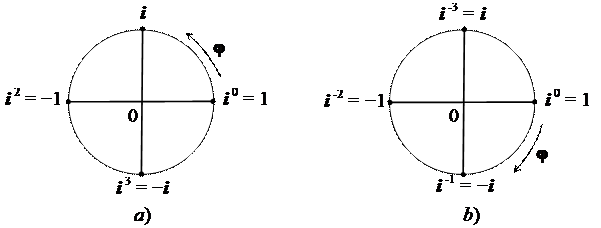Рис. 1.11.

Функція

Рис.1.11.

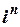приймає лише чотири значення. Так як число z = 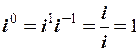, то загальна формула для визначення числа 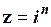при n ≥ 0 набуває вигляду:

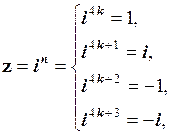(1.64)

де k = 0, 1, 2, ….

При збільшенні степеня на 4 число 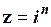повторює своє значення. Тому, будь-яке число n ділимо на 4, тоді ціла частина від ділення є число k. Наприклад:

.

При n < 0 процедура аналогічна (рис. 1.11, b). Так як множення на 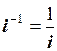, тобто рівносильне діленню на і, то число z треба повернути на кут 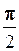за годинниковою стрілкою. Загальна формула числа при n < 0 має вигляд:

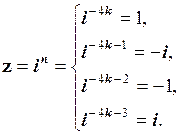(1.65)

Наприклад:

.

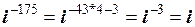Порівнюючи формули (1.64) та (1.65) та користуючись рис. 1.11, а та рис. 1.11, b, бачимо, що для парних n: 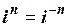, а для непарних n: – .

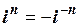Приклад 1.2. Спростити вираз .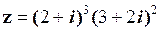

Розв’язування. Дії множення та піднесення до степеня комплексних чисел, що задані в алгебраїчній формі, будемо виконувати за правилами множення алгебраїчних многочленів. Спочатку кожний множник піднесемо до степеня і спростимо, а потім результати перемножимо.

.

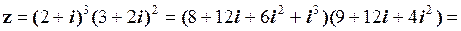
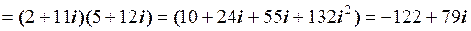Зауважимо, що будь-який проміжний результат є комплексним числом, а отже, зводиться до двочлена. Тому алгебра многочленів комплексних чисел зводиться до алгебри двочленів.

Приклад 1.3. Записати вираз 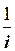в алгебраїчній формі.

Розв’язування. Помноживши чисельник та знаменник на i, одержимо:

.

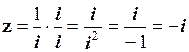Приклад 1.4. Записати число 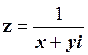в алгебраїчній формі.

Розв’язування. Помножимо чисельник та знаменник на число 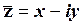, яке є спряженим до числа 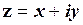, що стоїтьв знаменнику, а потім скористаємося формулою (1.54):

.

Реальна частина: 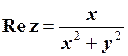, уявна частина: .

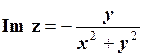Приклад 1.5. Записати число в тригонометричній формі.

Розв’язування. Тригонометрична форма комплексного числа має вигляд

,

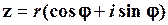де модуль числа z згідно (1.6) дорівнює

.

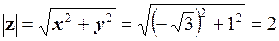Так як 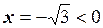, а 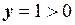, то головне значення аргументу згідно формули (1.17) дорівнює:

.

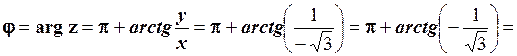
Отже,

.

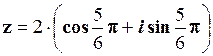Приклад 1.6. Записати число 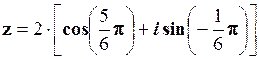в тригонометричній формі.

Розв’язування. Спочатку числу z надамо алгебраїчної форми:

.

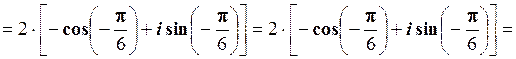
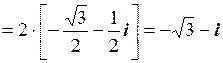Модуль числа z дорівнює:

.

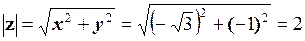Так як 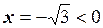, а 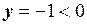, то згідно (1.17):

.

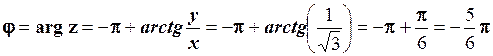Таким чином, .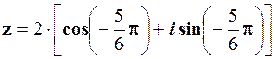

Приклад 1.7. Записати число 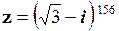в алгебраїчній формі.

Розв’язування. Спочатку число 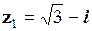запишемо в тригонометричній формі, а потім скористаємося формулою Муавра.

.

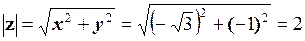Так як 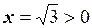, то згідно (1.17):

.

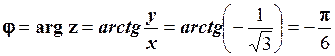Отже,

.

Згідно формулам (1.29) та (1.30)

.

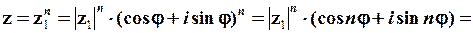
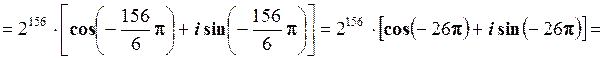
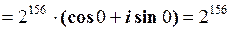Було відкинуто ціле число повних обертів кута 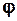. Так як –26 = 13(–2 π), то було відкинуто 13 обертів за годинниковою стрілкою.

Приклад 1.8. Знайти всі значення кореня .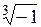

Розв’язування.

.

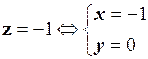Отже, .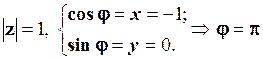

Таким чином, тригонометрична форма числа z набуває вигляду:

.

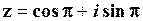Згідно формулам (1.33), (1.34) та (1.35)

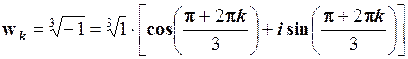, k = 0, 1, 2.

n = 3, .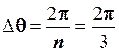

При відповідних значеннях k корені дорівнюють:

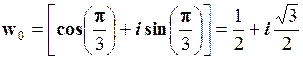, при k = 0;

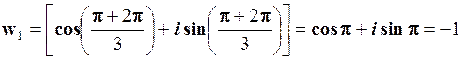, при k = 1;

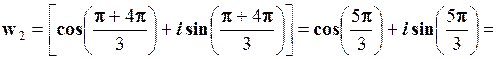
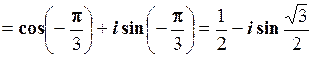, при k = 2.

Всі три корені зображені на рис.1.12.

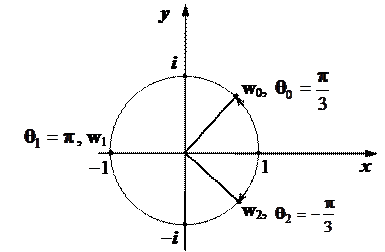Рис. 1.12.

Приклад 1.9. Записати в показниковій формі комплексне число .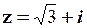

Розв’язування. Згідно формули (1.43)

.

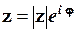Знайдемо модуль 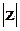та головне значення аргументу j = arg z числа z.

.

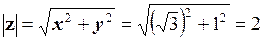Так як 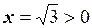, то згідно (1.17):

.

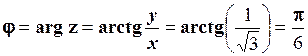Отже,

.

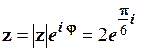Приклад 1.10. Розділити число 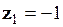на число .

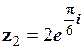Розв’язування. Запишемо число 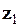в показниковій формі. Так як 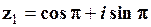(див. приклад 1.7), то .

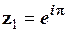Згідно формули (1.47):

.

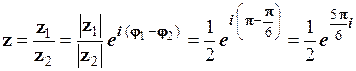Дата добавления: 2014-12-23