
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема «Технология компьютерного 1 страница
|
|
|
|
математического моделирования»
Целесообразно вводные занятия по этой теме проводить в виде беседы, привлекая знания учеников по различным общеобразовательным дисциплинам, их жизненный опыт. Изложение необходимо иллюстрировать большим количеством примеров.
Особая роль первого раздела заключается в том, что здесь повторяются и обобщаются основные понятия компьютерного математического моделирования (КММ), известные из базового курса информатики, вводятся новые — «моделирование», «информационное моделирование», «математическое моделирование», «формализация», «идентификация модели» и др.
Другой важный аспект темы — формирование представления об этапах компьютерного математического моделирования. Здесь, с одной стороны, фигурируют приведенные выше понятия, с другой — присутствует полная технологическая цепочка КММ. Конечно, все эти этапы будут неоднократно повторяться при исследовании конкретных процессов (объектов), но основы закладываются именно на вводных занятиях. Действительно, одним из условий успешного усвоения учащимися систематического курса КММ является наличие у них хорошо развитых представлений об этапах КММ, о значении каждого из этапов.
При обсуждении этапов КММ можно использовать общую схему абстрактного моделирования, изображенную выше на рис. 13.4. Обсуждение следует конкретизировать, учитывая особенности именно математического моделирования.
Формализованная схема является промежуточным звеном между содержательным описанием и математической моделью и разрабатывается в тех случаях, когда из-за сложности исследуемого процесса переход от содержательного описания к математической модели оказывается невозможным. На этапе построения формализованной схемы должна быть дана точная математическая задача исследования с указанием окончательного перечня искомых величин и оцениваемых зависимостей.
Прежде всего составляется список величин, от которых зависит поведение объекта или ход процесса, а также список тех величин, которые желательно получить в результате моделирования.

где Fj - символически обозначает некоторые математические операции над входными величинами.
Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием. Чаще всего невозможно, да и не нужно, учитывать все факторы, которые могут повлиять на значения интересующих нас величин yj. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Отбрасывание менее значимых факторов огрубляет модель и способствует пониманию главных свойств и закономерностей объекта моделирования.
На этапе перехода от формализованной схемы к математической модели необходимо перейти от абстрактной формулировки к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстанет перед нами в виде уравнения, системы уравнений, неравенств, матриц, дифференциальных уравнений и т. д.
В беседе следует подчеркнуть тот факт, что математическое моделирование отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т.е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Возможности аналитических методов решения сложных математических задач, однако, очень ограничены и, как правило, гораздо сложнее численных. Поэтому при проведении занятий по КММ в школе следует пользоваться численными методами, реализуемыми на компьютерах. Это создает определенное методическое единство курса и заметно снижает барьер необходимой математической подготовки учащихся. Разумеется, и в численные методы при профессиональном занятии математическим моделированием приходится углубляться настолько, что при этом требуется значительное математическое образование, но можно попытаться в школьной практике ограничиться лишь простейшими из них.
И, наконец, после изучения этого раздела учащиеся должны уяснить подходы к классификации компьютерных математических моделей. Как известно, бывают классификации моделей по используемому математическому аппарату, по отраслям наук и т.д. Наиболее органичной представляется классификация по целям моделирования. Действительно, выделение целей моделирования — это первое, что необходимо сделать перед содержательным описанием и формализацией объекта (процесса), и в конечном итоге именно цели моделирования определяют, какая модель будет построена. При этом важно подчеркнуть, что в зависимости от целей моделирования и выбранных факторов для одного и того же процесса можно получить существенно различающиеся математические модели. Учителю следует привести примеры постановки задач, приводящих к моделям, относящимся к основным классам: дескриптивным, оптимизационным, многокритериальным, игровым, имитационным.
Тема «Моделирование физических процессов»
Эта тема фигурирует в нескольких вариантах курса компьютерного моделирования. Причина — традиции и относительная простота решаемых задач, их близость школьному курсу физики.
Как правило, эта тема является началом к изложению компьютерного моделирования в физике. Поэтому ей может предшествовать вводная лекция (беседа) о компьютерном моделировании физических процессов в целом.
В начале на ряде примеров проиллюстрируйте утверждение, что физика — наука, в которой математическое моделирование является чрезвычайно важным методом исследования. Причину этого в целом можно сформулировать так: при максимальном проникновении в физику математических методов, порой доходящем до фактического сращивания этих наук, реальные возможности решения возникающих математических задач традиционными методами очень ограничены.
Во многих вариантах курса компьютерного моделирования математические модели в физике по праву занимают больший объем по сравнению с другими, и на их изучение отводится большее количество времени. Действительно, создание той или иной модели физического процесса является естественным и не требует некоторых искусственных приемов, к которым часто приходит прибегать в других предметных областях. Поэтому восприятие этих математических описаний процессов или явлений не вызывает у учащихся, по крайней мере, психологических трудностей. В профильном курсе, ориентированном на учащихся, специализирующихся по физико-математическому и естественнонаучному профилю, целесообразно наибольшее внимание уделить именно моделям физики.
Перечень рассматриваемых вопросов может быть таков:
• движение тел с учетом сопротивления среды;
• движение маятника с учетом сопротивления среды, вынужденные колебания, резонанс и т.д.;
Обозначив первые (входные) величины через х1, х2,..., хn, а вторые (выходные) через y1, у2,..., yk, можно поведение объекта или процесса символически представить в виде
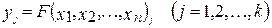
• движение небесных тел (задача двух тел);
• движение электрических зарядов;
• тепломассоперенос (на примере процесса теплопроводности в линейном стержне).
Номенклатура компьютерных математических моделей в физике может ориентироваться на подготовленность и интересы учащихся, их специализацию в том или ином разделе физики.
Цели обучения: t
• ввести в КММ на примере моделей из области физики;
• отработать схемы вычислительного эксперимента на сравнительно простых, знакомых по курсу физики задачах.
Поставленные задачи обучения считаются успешно выполненными, если у учащихся вырабатывается комплекс указанных ниже знаний, умений и навыков.
Изучение каждой новой содержательной задачи и, как следствие, получение новой математической модели требует мотивировки целесообразности ее введения. Мотивировка может, во-первых, опираться на жизненный опыт учащихся, во-вторых, достигаться путем разрешения проблемной ситуации.
Моделирование процессов движения тел в среде. При моделировании процесса движения тела, прежде всего, целесообразно рассмотреть традиционные для школьного курса физики динамические модели, но с учетом сопротивления среды. Это свободное падение тела, полет тела, брошенного под углом к горизонту, движение тела с переменной массой. При этом составляющие силы сопротивления можно рассмотреть предварительно, перед изучением конкретных моделей либо в ходе построения одной из моделей.
Более детально обсудим методику построения компьютерных математических моделей физических процессов и их последующего исследования на примере нескольких задач.
Первая из них — моделирование свободного падения тела с учетом сопротивления среды. Основная дидактическая роль этой наиболее простой задачи — практическое знакомство с этапами компьютерного математического моделирования, освоение этих этапов, приобретение навыков формулирования и разрешения учебных проблем, проблемных ситуаций. Несмотря на то, что на первый взгляд она является простой, при ее исследовании придется решить ряд серьезных проблем, о чем будет сказано ниже.
В ходе обучения обязательно придется пользоваться понятиями «предел» и «производная». Понятие «предел» не вызывает существенных затруднений; в контексте данного обсуждения вполне достаточно интуитивного понимания предела, сформированного у учащихся к X классу.
Не совсем так обстоит дело с понятием «производная». Возможны две ситуации:
1) учащиеся вполне владеют понятием и дифференциальная форма записи второго закона Ньютона (и последующих при решении конкретных задач дифференциальных уравнений) будет им понятна (при этом никакой техники дифференцирования, тем более решения дифференциальных уравнений, не требуется);
2) учащиеся не знакомы с этим понятием; в этом случае необходимо сделать математическое отступление и пояснить понятие «производная», на что, как показывает опыт, вполне достаточно одного урока.
Другая методическая проблема, которую необходимо решить, — ,t строить модели динамических процессов в виде дифференциальных или конечно-разностных уравнений. Как показывает практика, учащиеся физико-математических классов вполне способны воспринять дифференциальные уравнения и численные методы их решения. Для этого достаточно ввести дифференциальные уравнения и объяснить простейшие численные методы их решения, базируясь на физическом и геометрическом смысле производной.
При использовании численных методов интегрирования дифференциальных уравнений разумно рассмотреть явные схемы невысокого порядка (не выше второго); если кто-либо из учащихся проявит интерес именно к методам решения систем дифференциальных уравнений и их устойчивости, то следует предложить им самостоятельно изучить литературу, где излагаются явные ме-тоды более высокого порядка либо неявные схемы. Такой подход (подтвердил свою жизнеспособность.
При изучении динамических процессов в менее подготовленной аудитории рекомендуется ограничиться конечно-разностными уравнениями. Любую модель из рассмотренных ниже можно сформулировать в конечно-разностном виде, вообще не упоминая о дифференциальных уравнениях (примеры далее приводятся).
Свободное падение тела с учетом сопротивления среды. В этой и многих других физических задачах, на основе которых строятся модели, фундаментальную роль играет второй закон Ньютона — основа динамики. Формулируем его вначале в «школьной» форме  , а затем, чтобы исследовать реалистические ситуации, необходимо подвести учащихся к более общей математической форме. Проводим следующее рассуждение: если движение происходит с переменной скоростью, то, как известно учащимся, для его характеристики привлекаются два понятия: средняя скорость за некоторый промежуток времени Dt, равная отношению —
, а затем, чтобы исследовать реалистические ситуации, необходимо подвести учащихся к более общей математической форме. Проводим следующее рассуждение: если движение происходит с переменной скоростью, то, как известно учащимся, для его характеристики привлекаются два понятия: средняя скорость за некоторый промежуток времени Dt, равная отношению — 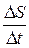 , где DS — пройденный путь и мгновенная скорость в данный момент времени t, которая на математическом языке записывается как
, где DS — пройденный путь и мгновенная скорость в данный момент времени t, которая на математическом языке записывается как  . Точно так же при движении с постоянным ускорением можно ввести два понятия — среднее ускорение за время Dt, равное
. Точно так же при движении с постоянным ускорением можно ввести два понятия — среднее ускорение за время Dt, равное  , и мгновенное ускорение в момент t:
, и мгновенное ускорение в момент t: 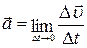 .
.
В стандартных математических обозначениях 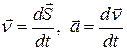 , т. е. мгновенная скорость есть производная от перемещения по времени, а мгновенное ускорение — производная от скорости по времени. Второй закон Ньютона в уточненной редакции утверждает: ускорение, с которым движется тело в данный момент времени, пропорционально действующей на него в этот момент силе и обратно пропорционально имеющейся в данный момент у тела массы:
, т. е. мгновенная скорость есть производная от перемещения по времени, а мгновенное ускорение — производная от скорости по времени. Второй закон Ньютона в уточненной редакции утверждает: ускорение, с которым движется тело в данный момент времени, пропорционально действующей на него в этот момент силе и обратно пропорционально имеющейся в данный момент у тела массы:
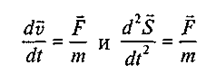 (1)
(1)
разные записи этого утверждения.
Приведенное рассуждение является типичным для этой темы обоснованием перехода от дискретного к непрерывному.
Далее отмечаем, что при реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Очевидно, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды.
Поясните учащимся, что закономерности, связывающие силу сопротивления со скоростью движения тела, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. Приведите эти закономерности (при этом вполне достаточно ограничиться линейной и квадратичной по скорости составляющими силы сопротивления:
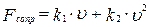 .
.
Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения — это уравнение второго закона Ньютона с учетом двух сил, действующих на тело — силы тяжести и силы сопротивления среды. Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем:
 (2)
(2)
При выводе уравнения целесообразно изобразить на рисунке силы, действующие на тело; это будет способствовать наилучшему восприятию полученного уравнения и не вызовет дополнительных вопросов.
Вопрос, который следует обсуждать на первом этапе, таков: каков характер зависимости скорости от времени, если все параметры, входящие в последнее уравнение, заданы? При такой постановке модель носит сугубо дескриптивный характер.
На этом этапе возникает вопрос о способах решения дифференциальных уравнений. Очевидный ответ: универсальные методы их решения — численные. Для начала вполне достаточно ограничиться методом Эйлера. Проводим следующее рассуждение: если на основании определения производной заменить ее в уравнении (2) конечно-разностным отношением 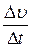 , то, зная скорость v0 в начальный момент времени t = 0 и обозначив ее как v 1в момент Dt, перепишем уравнение в виде
, то, зная скорость v0 в начальный момент времени t = 0 и обозначив ее как v 1в момент Dt, перепишем уравнение в виде
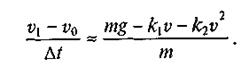 (3)
(3)
Если далее понимать под v} приближенное значение скорости в момент Dt, то получим формулу для вычисления v1:
 (4)
(4)
Это и есть формула метода Эйлера.
Далее рассуждение ведется по индукции. Располагая значением v1 можно, отталкиваясь от него, найти v2 и т.д. Общая формула метода Эйлера применительно к данной задаче такова:
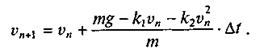 (5)
(5)
Возникает следующая проблема: до каких пор проводить расчеты? В данной задаче естественным представляется ответ: до падения тела на землю. Для обнаружения этого события необходимо рассчитывать не только скорость, но и пройденный путь. Поскольку перемещение связано со скоростью соотношением 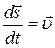 , то, проводя схожие с приведенными выше рассуждения, приходим ко второму разностному уравнению sn+l = sn + vn×Dt, решаемому одновременно с первым. Иначе говоря, мы применили метод Эйлера к системе дифференциальных уравнений. Решая эту систему при заданных начальных условиях v(0) = v0, s(0) = s0, получим таблицу значений функций v(t), s(t).
, то, проводя схожие с приведенными выше рассуждения, приходим ко второму разностному уравнению sn+l = sn + vn×Dt, решаемому одновременно с первым. Иначе говоря, мы применили метод Эйлера к системе дифференциальных уравнений. Решая эту систему при заданных начальных условиях v(0) = v0, s(0) = s0, получим таблицу значений функций v(t), s(t).
Важные, тесно связанные между собой методическая и содержательная проблемы — это контроль точности и выбор шага по времени D t. Казалось бы, чем меньше шаг, тем точнее решение, но, во-первых, это утверждение не является вполне верным (причины обсудим ниже), а во-вторых, при очень мелком шаге расчетов «результатов» слишком много и они становятся необозримыми. Отсюда возникает еще одна методическая проблема: как выбрать шаг по времени для вывода значений перемещения и скорости на экран. Этот шаг выбирается из соображений разумной достаточности информации и обозримости представления результатов на экране; из практических соображений удобно, если он кратен D t (реально шаг вывода результатов может составлять десятки и сотни D t).
Кроме того, ставится задача: представить полученные результаты в наиболее удобном для восприятия виде. Это могут быть графики зависимостей v(t), s(t); изображение процесса падения в динамике (здесь возможны вариации).
Как отмечалось выше, если математическая подготовка учащихся недостаточна, проводить моделирование на основе дифференциальных уравнений затруднительно и нецелесообразно. Возможный выход — использование конечно-разностных уравнений. К построению модели и учету факторов, влияющих на изучаемое явление или процесс, подходим на должном уровне строгости, но предельный переход не выполняем, останавливаемся и записываем вместо дифференциальных соответствующие конечно-разностные уравнения. Проведем соответствующее несложное рассуждение, в котором упоминание о дифференциальных уравнениях отсутствует полностью.
Вспомним, что ускорение есть приращение скорости, а скорость — приращение перемещения:  . Знаки приближенного равенства свидетельствуют о том, что эти соотношения тем точнее, чем меньше промежуток D t; в пределе D t ® 0 они становятся точными.
. Знаки приближенного равенства свидетельствуют о том, что эти соотношения тем точнее, чем меньше промежуток D t; в пределе D t ® 0 они становятся точными.
Если в некоторый момент времени t0 величина s имеет значение s0, а величина v — значение v 0, то в некоторый последующий момент времени t1 = t0 + Dtбудем иметь:
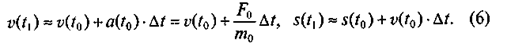
Здесь введены обозначения F0 = F(t0, v0, s0), m0 = m(t0, v0, s0).
При вычислениях значений v и s в последующие моменты времени можно поступать аналогично (6). Так, если известны значения vi и si в момент ti, то
 (7)
(7)
На самом деле мы, естественно, пришли к формулам метода Эйлера, но методически иначе, даже не упоминая о дифференциальных уравнениях.
При построении этой и подобной ей моделей следует обратить внимание учащихся на то, что в разбиении непрерывного времени на отрезки длиной D t проявляется одна из фундаментальных идей информатики об универсальности дискретной формы представления информации, отраженная как в конструкции компьютера, так и во множестве приложений информатики.
Вопрос о выборе конкретного значения D t весьма непрост и определяется следующими соображениями. При компьютерном моделировании мы можем получить решение задачи о движении тела на некотором конечном отрезке времени [t0, Т].Чем меньше величина D t:
а) тем больше вычислений требуется, для того чтобы пройти весь заданный временной интервал;
б) тем выше точность в передаче значений непрерывных функций s(t), v(t) их дискретными представлениями — наборами чисел si = s(ti), vi = v(ti).
Вопрос о точности результатов является в описываемом моделировании одним из центральных. Он распадается на два: как оценить эту точность и можно ли, уменьшая D t, достигать все большей точности?
Остановимся вначале на первом. Теоретические оценки точности слишком сложны и на практике часто неприменимы. Самый популярный эмпирический прием оценки точности заключается в следующем: отрезок [t0, Т]проходится с некоторым шагом D t, а затем с существенно меньшим (например, в два раза) шагом. Сравнение результатов в точках t1, t2,..., T позволяет составить представление о реальной точности результатов. Если она недостаточна, то следует повторить процесс с еще меньшим шагом.
Однако уменьшение D t, как ни странно, не всегда ведет к улучшению результатов моделирования. Одна из причин в том, что чем меньше шаг, тем больше арифметических действий и тем больше шансов увеличить чисто вычислительную погрешность округления, всегда сопутствующую компьютерным вычислениям. Другая причина глубже и связана со способом дискретизации — перехода от описания реально непрерывного процесса движения тел к описанию по простейшим формулам (4) — (7). Обе вместе могут привести к неустойчивости решения, т. е. получению результатов, не имеющих реально ничего общего с истинными. Обычно неустойчивость становится заметной при повторениях процесса с уменьшением шага D t. Способы дискретизации, ведущие к более устойчивым методам решения таких задач, описаны в литературе (см., в частности, [5, 9]).
Отметим, что существует немало компьютерных программ, моделирующих простые физические процессы. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако при их использовании остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как иллюстративные. Поэтому более целесообразно нацеливать учащихся на самостоятельную разработку программ.
В некоторых случаях для ускорения процесса работы над какой-либо задачей целесообразно вместо составления программы воспользоваться прикладной программой (например, табличным процессором или математическим пакетом типа MathLab, что, впрочем, уже потребует дополнительных усилий).
Для того чтобы продемонстрировать учащимся практическую значимость решаемых задач, построенных математических моделей, целесообразно предложить содержательную проблему, для решения которой необходимо применить построенную модель, предварительно формализовав задачу и выполнив ранжирование факторов. В качестве такой содержательной задачи может, например, выступать задача о полете парашютиста. Проведем детальное моделирование. Перед тем как его начинать, необходимо решить вопрос об удобных способах представления результатов. Разумеется, колонка чисел, выдачи которой проще всего добиться от компьютера при численном моделировании, желательна. Однако слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым интегрируется дифференциальное уравнение, т.е. далеко не все значения vh найденные компьютером, следует записывать в результирующую таблицу.
Кроме таблицы необходим график зависимости v(t); по нему хорошо видно, как меняется скорость со временем, т.е. происходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Изображениям в разные моменты можно придать разный цвет — от «холодного» зеленого при относительно малых скоростях до «горячего» красного при высоких скоростях — прием условных цветов, широко используемый в современной научной графике.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом — скажем, через каждый метр или 100 метров, смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются.
Решение будем выполнять до тех пор, пока парашютист не опустится на землю. Шаг интегрирования дифференциального уравнения можно подобрать методом проб и ошибок, решая уравнение несколько раз, начав, например, с заведомо большого значения D t = 0,1 с и постепенно уменьшая его до тех пор, пока качество решения не станет приемлемым.
Полное моделирование включает изучение временной зависимости не только скорости, но и пройденного телом пути. Не сделав последнего, можно в конкретных ситуациях получить бессмысленный физически результат. Например, парашютист прыгает с самолета и через некоторое время достигает вполне безопасной для приземления скорости 10 м/с. Но сколько он перед этим пролетел? Если это расстояние много больше высоты, с которой состоялся прыжок, то фактическая скорость приземления много выше, и это ничего хорошего не сулит.
Компьютерная реализация этой модели может быть выполнена программированием как на традиционном языке программирования (Паскаль, Бейсик и др.), так и, например, в электронных таблицах. Частичное тестирование программ можно проводить при k2 = 0, т.е. для движения без трения. Решение в этом случае очевидно (свободное падение).
Как отмечалось выше, методически целесообразным бывает использование табличных процессоров для моделирования. Результаты решения подобных задач обязательно следует иллюстрировать графиками зависимости скорости и перемещения от времени (если же движение неодномерно, тот и изображениями траекторий). Разумеется, предпочтительным является построение графиков программным путем. Если учащиеся реализуют программы на языке программирования, то проще всего заложить в программу еще и построение графиков; если решение реализуется в электронной таблице, то можно воспользоваться заложенными в эти программы графическими возможностями.
Следует заметить, что для хранения результатов расчетов в данном случае требуется очень много ячеек таблицы, и хотя современные табличные процессоры позволяют хранить большой объем информации, в случае нехватки памяти рекомендуется увеличить шаг, с которым проводятся вычисления (снизив при этом точность вычислений). Табличный процессор позволяет представлять результаты расчетов и в графической форме. Можно при работе над задачей получить результаты двумя способами: с помощью табличного процессора и составлением собственной программы — для того, чтобы затем сравнить эти результаты и временные затраты каждого из способов.
Модели свободно падающего тела можно придать черты оптимизационной, поставив задачу, например, так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Или по-другому: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k2), чтобы скорость приземления была безопасной? Выполнение таких исследований многократно более трудоемко, нежели просто изучение одного прыжка при заказанных условиях.
Таким образом, в методическдм плане рассмотренная модель выигрышна, поскольку, несмотря на свою простоту, позволяет обсуждать множество связанных с ней проблем.
При выполнении компьютерной лабораторной работы по исследованию модели можно предложить разноуровневые учебные задания (рассчитанные, соответственно, на «среднего» и «сильного» ученика):
1) получить результаты и их графическое отображение для заданного набора параметров модели;
2) исследовать свободное падение тела в средах различной вязкости и провести содержательное сравнение результатов исследования;
3) придать модели черты оптимизационной (самостоятельно или с помощью учителя), выполнить указанные исследования, провести содержательное сравнение результатов исследования.
По использованной здесь схеме могут вводиться и исследоваться другие модели, где учитывается сопротивление среды. При этом уже нет нужды отвлекаться на изучение численных методов решения систем дифференциальных уравнений, поскольку это достаточно проделать аккуратно только один раз, скажем, на примере рассмотренной выше модели.
Перечислим модели движения тела в среде, которые допускают достаточно простое исследование:
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 688; Нарушение авторских прав?; Мы поможем в написании вашей работы!