Тема «Технология компьютерного 3 страница

В рассмотренной задаче, как и в любой более сложной задаче об очередях, может возникнуть критическая ситуация, когда очередь неограниченно растет со временем. В самом деле, если люди заходят в магазин очень часто (или продавец работает слишком медленно), то очередь начинает нарастать, и в любой системе с конечным временем обслуживания наступит кризис. Моделирование приближения к критической ситуации по мере возрастания одного из параметров — интересная исследовательская задача.

На примере задачи об очереди отрабатываются сразу несколько новых понятий и навыков, таких как:

• понятие о случайных процессах;

• понятие и простейшие навыки имитационного моделирования;

• построение оптимизационных имитационных моделей;

• построение многокритериальных моделей (путем решения задач о наиболее рациональном обслуживании покупателей в сочетании с интересами владельца магазина).

Тема «Моделирование динамики развития популяций»

В данной теме ограничимся обсуждением методики проведения занятий по моделированию некоторых процессов, составляющих основу классической экологии (т.е. процессов развития отдельных популяций и их взаимодействия). В такой постановке этот материал может быть полезен для проведения нескольких уроков в пределах предмета, в котором моделирование экологических процессов является не основой, а частью. Такой выбор обусловлен следующими причинами. Во-первых, соответствующие модели достаточно просты и изучены, постановка их вполне очевидна и в познавательном плане интересна и полезна. Во-вторых, модели распространения загрязнений окружающей среды, которые успешно применяют в современной социальной экологии, требуют использования весьма сложного математического аппарата, да и сами еще не вполне устоялись.

С другой стороны, возможны профильно-ориентированные на экологию курсы информатики. Для таких курсов рассматриваемого в данном параграфе материала недостаточно. Дополнительный материал на эту тему можно найти, к примеру, в пособиях [25, 30].

Вводная беседа в этой теме может быть посвящена введению в проблематику классической экологии и использование в ней математических моделей. Следует дать определения таким понятиям, как «популяция», «сообщество», «внутривидовая конкуренция», «межвидовая конкуренция».

Математические модели в экологии используются практически с момента возникновения этой науки. И хотя поведение организмов в живой природе гораздо труднее адекватно описать средствами математики, чем самые сложные физические процессы, модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Кажется удивительным, что люди, занимающиеся живой природой, воссоздают ее в искусственной математической форме, но есть веские причины, которые стимулируют эти занятия. Вот основные цели создания математических моделей в классической экологии:

1. Модели помогают выделить суть или объединить и выразить с помощью нескольких параметров важные разрозненные свойства большого числа уникальных наблюдений, что облегчает экологу анализ рассматриваемого процесса или проблемы.

2. Модели выступают в качестве «общего языка», с помощью которого может быть описано каждое уникальное явление, и относительные свойства таких явлений становятся более понятными.

3. Модель может служить образцом «идеального объекта» или идеализированного поведения, при сравнении с которым можно оценивать и измерять реальные объекты и процессы.

Модель считается адекватной рассматриваемому явлению только в том случае, если она выполняет одну из указанных выше функций.

При проведении беседы следует обратить внимание учащихся на то, что привлечение компьютеров существенно раздвинуло границы моделирования экологических процессов. С одной стороны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического исследования, с другой — возникли принципиально новые направления, и прежде всего — имитационное моделирование.

После вводной лекции приступаем к построению и исследованию конкретных моделей. Методически уместно начать это с рассмотрения развития популяций с дискретным размножением, после чего следует плавный переход на популяции с непрерывным размножением. Естественная последовательность рассмотрения такова:

• динамическое моделирование численности изолированной популяции с дискретным размножением:

а) при отсутствии внутривидовой конкуренции;

б) при наличии внутривидовой конкуренции;

• динамическое моделирование численности изолированной популяции с непрерывным размножением:

а) при отсутствии внутривидовой конкуренции;

б) при наличии внутривидовой конкуренции;

• динамическое моделирование взаимодействия популяций:

а) состоящих в отношениях межвидовой конкуренции;

б) состоящих в отношениях «хищник— жертва»;

• имитационное моделирование развития популяции и взаимодействия популяций.

Примеры ряда моделей, обозначенных выше, можно найти в пособиях [5, 9, 22, 27, 30, 35]. Обсудим методику их построения и исследования на нескольких примерах.

Пример. Моделирование развития изолированной популяции с дискретным размножением с учетом внутривидовой конкуренции.

Рассматриваются биологические виды, для которых потомки и предки не сосуществуют во времени (многочисленные растения, насекомые и др.). Тогда последовательные значения численности популяции можно представить последовательностью N₀, N₁,....

Если нет никаких причин ограничения численности популяции, тогда возникает простейшая очевидная модель: N_t+1 = R×N_t, где R— коэффициент воспроизводства. Решение этой модели очевидно: N_t = N₀×R¹, ипри R >1 численность популяции нарастает по геометрической прогрессии.

Даже эта простейшая модель заслуживает обсуждения. Она выражает то, что в литературе иногда называют «законом Мальтуса».

Очевидно, что долго неограниченно возрастать популяция не может. Простейший способ учета внутривидовой конкуренции связан с гипотезой о том, что коэффициент воспроизводства не есть константа, а зависит от численности популяции, спадая по мере ее роста. На этом этапе следуют разъяснить учащимся методику построения моделей в сфере знаний, где основным способом исследования являются наблюдения, в которой точные математические законы отсутствуют в силу сложности системы (в отличие от, например, физики). В такой ситуации делаются достаточно произвольные допущения, в значительной мере оправдываемые простотой, а полезность модели определяется путем сопоставления ее решений с закономерностями поведения реальных систем.

Проиллюстрируем это простым соображением. Итак, надо учесть, что величина R монотонно спадает с ростом величины N. Реального вида этого спада мы не знаем; его можно представить множеством способов с использованием общеизвестных элементарных функций, а если надо, то и выходом из этого класса.

Модель, в основу которой положена простейшая из таких функций, выглядит следующим образом: 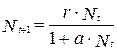. Методика исследования этой модели и ряда других описана в указанных выше пособиях. Полезность модели следует их того, что описываемое ею поведение численности популяций многократно наблюдалось экологами в природе.

После этого ставим вопрос: достаточно ли этой модели для качественного описания развития любой популяции с дискретным размножением? Ответ может последовать лишь из того, наблюдались ли качественно иные динамики развития таких популяций, и является положительным. В природе наблюдались существенно более сложные процессы, нежели монотонное возрастание численности популяций с выходом на стационар, предсказываемое описанной выше моделью. Поэтому продолжился поиск более адекватных моделей.

В частности, целесообразно рассмотреть модель, предсказывающую четыре качественно разных типа динамики численности популяций (в зависимости от соотношения значений параметров): монотонное возрастание с выходом на стационар, колебательное установление стационарной численности, регулярное колебательное изменение (так называемые предельные циклы) и хаотическое поведение без каких-либо видимых закономерностей. Все эти типы динамик наблюдаются в природе.

Методика изучения сложных движений зависит от математической подготовки учащихся. Чаще всего предельные циклы и хаотическое поведение приводим описательно, иллюстративно, не стремясь дать определение этим сложным процессам. В классах же с высоким уровнем математической подготовки и выраженным интересом учащихся обсуждение этих вопросов может быть существенным элементом развития математических интересов.

При изучении более сложных моделей, выраженных дифференциальными уравнениями, методика исследования в основном остается та же. Она включает следующие этапы:

• постановку проблемы, введение терминологии, описание поведения соответствующих природных систем;

• построение математической модели;

• попытку качественного исследования модели, включая построение диаграмм на фазовой плоскости параметров модели;

• численное решение дифференциальных уравнений (как правило, простейшими из методов либо путем использования готовых программ).

Совсем иной является методика построения имитационных моделей экологических процессов. Ограничимся формулировкой одной из задач [5], на которой можно отработать построение такой модели.

Пример. Разработать имитационную модель системы «хищник — Жертва» по следующей схеме.

«Остров» размером 20x20 заселен дикими кроликами, волками и волчицами. Имеется по несколько представителей каждого вида. Кролики в каждый момент времени с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов не окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и получает одно очко. В противнем случае она теряет 0,1 очка.

Волки и волчицы с нулевым количеством очков умирают.

В начальный момент времени все волки и волчицы имеют 1 очко.

Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда если волчица находится в одном из восьми близлежащих квадратов, волк гонится за ней.

Если волк и волчица окажутся в одном квадрате и там нет кролика, которого нужно съесть, они производят потомство случайного пола.

Пронаблюдайте за изменением популяции в течение некоторого периода времени. Проследите, как сказываются на эволюции популяций изменения параметров модели.

Дата добавления: 2014-12-27