
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ВВЕДЕНИЕ. Содержание Введение .. Тема 1 Операции над векторами и матрицами
|
|
|
|
Николаев В.С.
«МАТЕМАТИКА»
Москва 2009
Содержание
| Введение……………………………………………………………………….. | |
| Тема 1 Операции над векторами и матрицами.............................................. | |
| Тестовые задания по теме 1. ………………………………………………… | |
| Тема 2 Системы линейных алгебраических уравнений …………………… | |
| Тестовые задания по теме 2. ………………………………………………… | |
| Заключение …………………………………………………………………... | |
| Литература …………………………………………………………………… |
http://www.gaudeamus.omskcity.com/PDF_library_economic_5.html
(электронная библиотека по ЭММ)
В учебном пособии представлен краткий курс высший математики, который будет полезен студентам, не математического профиля (ЕН Ф.01). В пособии изложены основные понятия, формулы и методы высшей математики, представлены решения типичных задач, предложены задачи и тестовые задания для самостоятельной работы и проверки своих знаний, которые будет полезны и при сдаче зачетов и экзаменов, а также представлены варианты для контрольных работ.
Учебное пособие написано в соответствии с требованиями государственных стандартов высшего образования по высшей математике для экономических специальностей. В программу высшей математики входят линейная алгебра с элементами аналитической геометрии, дифференциальное и интегральное исчисления, ряды, дифференциальные уравнения, теория вероятностей и математическая статистика и экономико-математические модели.
Во все темы учебного пособия вошли основные понятия, определения, методы расчетов и решения типовых задач. В связи с тем, что экономистам в основном нужно знать приложения высшей математики в экономике, акцент ставится на таких примерах, задачах, моделей, которые имеют интерес с точки зрения экономической науки. Такие задачи есть во всех темах.
Студентам предлагается прочесть теоретическую часть каждой темы, обращая внимание на определения, свойства, описание методов расчета, решения задач и попытаться самостоятельно решить представленные в соответствующем параграфе задачи.
Тема №1 Операции над векторами и матрицами
§1.1 Матрицы
Любая статистическая таблица это пример матрицы. Таковой является, например следующая таблица:
Производство деталей за смену
| Детали, шт. | Бригады | |
| I | II | |
| А | ||
| Б | ||
| В |
Совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется прямоугольной матрицей размерности m ´ n.
þ Обозначения: Матрицы обозначаются прописными латинскими буквами A, B, C; элементы матрицы обозначаются строчными латинскими буквами, например, aij, i = 1,2,… m; j = 1,2, …n, где i показывает номер строки, j - номер столбца матрицы. Другими словами элемент матрицы aij - это элемент, находящийся на пересечении i –ой строки и j –ого столбца матрицы.
Общий вид прямоугольной матрицы записывается как
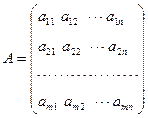 .
.
Матрица называется квадратной матрицей порядка n, если число строк m равно числу столбцов n.
При m = 1 матрица содержит одну строку и называется вектором-строкой. При n = 1 матрица содержит один столбец и называется вектором-столбцом. Элементы вектора называются также компонентами или координатами вектора.
Если все элементы прямоугольной матрицы нули (aij = 0), то матрица называется нулевой матрицей и обозначается буквой 0.
Если в квадратной матрице элементы главной диагонали равны единице (aii = 1), а все остальные элементы – нули (aij = 0, i¹j), то матрица называется единичной матрицей и обозначается как E.
Матрицы A и B равны, если равны все соответствующие элементы этих матриц aij = bij.
§1.2 Операции над матрицами
1. Сумма двух матриц. При сложении двух матриц A и B получается матрица C = A + B, элементы которой определяются как сумму соответствующих элементов этих матриц: cij = aij + bij. Из этого правила следует, что можно сложить только матрицы одинаковой размерности или одинакового порядка.
2. Умножение матрицы на действительное число. При умножении матрицы A на действительное число k получается матрица B = kA, элементы которой определяются умножением всех элементов матрицы B на это число: bij = kaij.
3. Умножение двух матриц. При умножении матриц A и B получается матрица C = A×B, элементы которой определяются по правилу 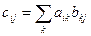 ; элемент i -й строки и j -го столбца матрицы C равен сумме произведений i -й строки матрицы A на соответствующие элементы j -го столбца матрицы B. Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Если матрицы A и B квадратные матрицы n –го порядка, то имеет смысл как произведение матриц A×B, так и произведение матриц B×A, причем полученные матрицы тоже n –го порядка. При этом в общем случае A×B ¹ B×A, т.е. произведение матриц не коммутативно.
; элемент i -й строки и j -го столбца матрицы C равен сумме произведений i -й строки матрицы A на соответствующие элементы j -го столбца матрицы B. Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Если матрицы A и B квадратные матрицы n –го порядка, то имеет смысл как произведение матриц A×B, так и произведение матриц B×A, причем полученные матрицы тоже n –го порядка. При этом в общем случае A×B ¹ B×A, т.е. произведение матриц не коммутативно.
@ Задача 1. Найти сумму матриц 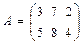 и
и 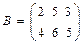 .
.
Решение: При сложении двух матриц суммируются все соответствующие элементы этих матриц:
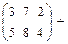
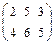
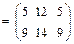 .
.
@ Задача 2. Найти произведение числа 4 и матрицы 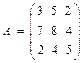 .
.
Решение: При умножении матрицы на число все элементы матрицы умножаются на это число:
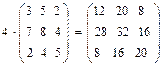 .
.
@ Задача 3. Найти произведение матриц  и
и  .
.
Решение: Элементы матрицы A×B определяются сложением произведений элементов первой строки матрицы А с соответствующими элементами первого столбца матрицы В, произведений элементов первой строки матрицы А с соответствующими элементами второго столбца матрицы В и т.д.:
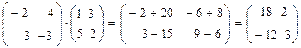 .
.
@ Задача 4. Найти произведение матриц 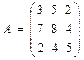 и
и 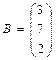 .
.
Решение: Элементы полученной матрицы представляют собой суммы произведений элементов строк матрицы А с элементами единственного столбца матрицы В:
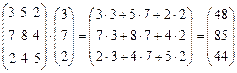 .
.
Свойства матриц
Если A, B и C матрицы, а k и m действительные числа, то выполняются следующие свойства.
1. Сумма матриц обладает свойством коммутативности: A + B = B + A.
2. Сумма трех матриц обладает свойством ассоциативности: (A + B) + C = A + (B + C).
3. Сумма матрицы A и нулевой матрицы 0 равна матрице A: A + 0 = A.
4. Сумма матрицы A и противоположной матрицы – A равна нулевой матрице 0: A – A = 0.
5. Произведение матрицы A и единичной матрицы E равно матрице A: EA = AE = A. При этом выполняется свойство коммутативности.
6. Сумма матриц обладает свойством дистрибутивности относительно действительного множителя (числа): k(A + B) = kA + kB
7. Произведение матрицы с двумя действительными множителями обладает свойством ассоциативности: k(mA) = (km)A.
8. Произведение матриц обладает свойством ассоциативности относительно действительного множителя: k(AB) = (kA)B.
9. Произведение трех матриц обладает свойством дистрибутивности: (AB)C = A(BC), A(B + C) = AB + AC, (A + B)C = AC + BC.
§ 1.3. Определители и их свойства
Определители
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 353; Нарушение авторских прав?; Мы поможем в написании вашей работы!