Определителем (детерминантом) квадратной матрицы n-го порядка называется число 3 страница

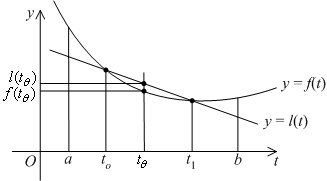
Если 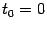и , то неравенство, означающее выпуклость функции 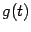, превращается в такое:

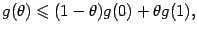
при всех .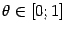

Дадим теперь определение выпуклой функции многих переменных.

Определение1 Пусть 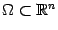- выпуклое множество, на котором задана функция 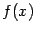. Функция 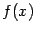называется выпуклой (или выпуклой книзу) на множестве 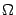, если для любых двух точек 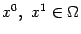функция 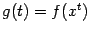, служащая ограничением функции 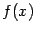на отрезок, соединяющий точк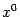и и 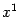, является выпуклой (книзу) функцией одного переменного 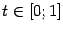(здесь, как и выше, ).

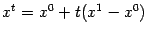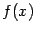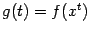Функция называется вогнутой (или выпуклой кверху) в , если функция вогнута.

Таким образом, функция 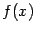вогнута в том и только том случае, когда функция 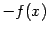выпукла.

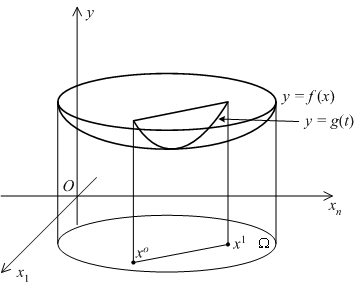
Выпуклость функции 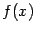в 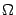означает, что для любого отрезка 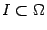с концам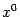и и 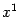параметризация этого отрезка в виде 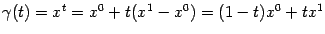задаёт композицию , являющуюся выпуклой функцией параметра 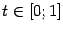. Ввиду выпуклости области 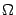, любые точк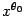и и 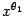отрезка 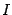лежат в 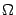, и их снова можно взять в качестве концов отрезка. Поэтому для выпуклости функции 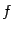в области 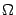необходимо и достаточно, чтобы неравенство

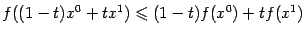
выполнялось при всех 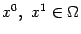и .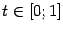

Если при этом при всех 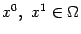и 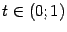выполняется строгое неравенство

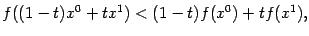
то функцию 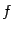будем называть строго выпуклой в .

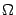Наконец, функция 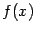называется строго вогнутой, если функция 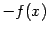строго выпукла; это означает выполнение строгого неравенства

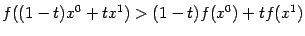
при всех 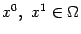и .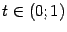

Геометрически (в случае 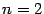) строгая выпуклость означает, что для любой хорды графика 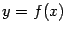точки дуги графика с теми же концами, что у хорды, лежащие в вертикальном сечении, проходящем через эту хорду, располагаются ниже точек хорды. Строгая вогнутость означает, что в любом вертикальном сечении график проходит выше любого отрезка, соединяющего две точки графика.

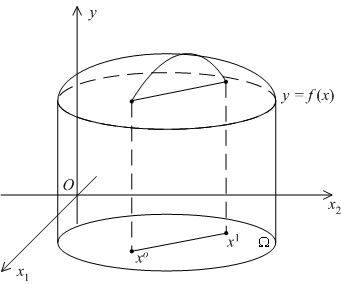
Заметим, что понятия выпуклой и вогнутой функций (а также строго выпуклой и строго вогнутой функций) в области 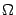определены только для выпуклых областей .

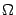Дадим теперь такое алгебраическое определение.

Определение: Пусть дана квадратная матрица 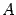размера 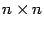. Она называется неотрицательно определённой, если 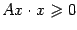для любого вектора-столбца 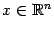(точкой обозначено скалярное произведение в 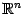). Матрица 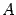называется положительно определённой, если 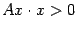для всех .

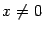Заметим, что выражение 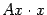можно записать в ви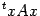де , где 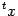- это матрица-строка, равная транспонированному столбцу 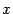. Вообще, верхний левый индекс 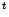мы будем применять для обозначения транспонированной матрицы.

Определение Квадратная матрица 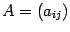называется симметричной, если при всех 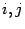имеет место равенство 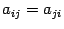, то есть если .

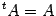У симметричной матрицы равны друг другу элементы, расположенные симметрично друг другу относительно главной диагонали матрицы.

Теорема: Пусть 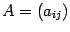- симметричная неотрицательно определённая матрица размера 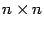. Тогда квадратичная функция (она же называется квадратичной формой, заданной матрицей )

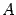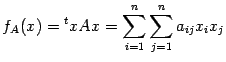
является выпуклой функцией (во всем пространстве, то есть при ).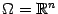

Если же симметричная матрица 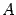- положительно определённая, то заданная ею квадратичная форма 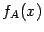является строго выпуклой.

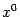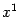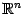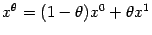Доказательство. Пусть и - две произвольные точки и , где 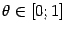, - точка отрезка, соединяющего 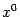с .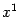

Предположим, что матрица 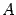неотрицательно определена. Элементарные преобразования позволяют записать 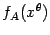в виде

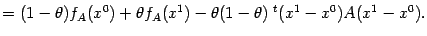
Поскольку матрица 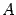неотрицательно определена, имеет место неравенство

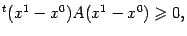
откуда сразу следует, что

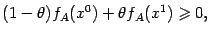
а это неравенство означает выпуклость функции .

Доказательство строгой выпуклости в случае положительно определённой матрицы проводится с помощью очевидных изменений приведённого доказательства.

Другой пример выпуклой функции даёт линейная функция:

Пример: Линейная функция

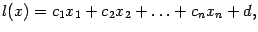
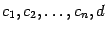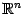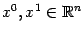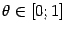где - постоянные, является выпуклой функцией во всём пространстве (но не является строго выпуклой функцией). Действительно, как легко проверить, при всех и имеем

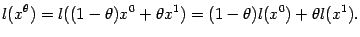
Поскольку функция 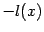, очевидно, также линейна, линейная функция 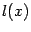является одновременно и вогнутой (но не строго вогнутой).

Если о некоторых функциях известно, что они выпуклы в области 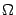, то из них можно сконструировать другие выпуклые функции, используя следующие свойства выпуклых функций.

Теорема: Пусть 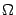- выпуклая область и функци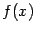и и 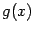выпуклы в . Тогда сумма этих функций 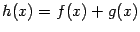также выпукла в .

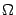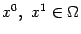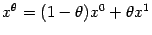Доказательство. Пусть и , где 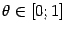. Тогда

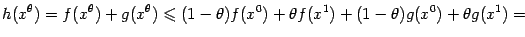
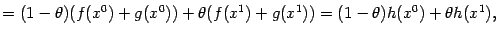
что и означает выпуклость функции .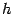

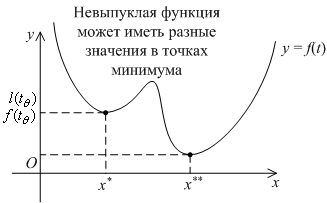
Практическая ценность этого утверждения в том, что при поиске наименьшего значения выпуклой функции в области достаточно найти любую точку локального минимума; во всех остальных точках локального минимума (если они существуют) значение функции будет точно такое же. Для невыпуклых функций это, конечно, не так, как видно на следующем рисунке:

Дата добавления: 2014-12-27