
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определителем (детерминантом) квадратной матрицы n-го порядка называется число 2 страница
|
|
|
|
Скалярное произведение
Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если один из векторов нулевой скалярное произведение считается равным нулю.
Скалярное произведение векторов  и
и  обозначается через
обозначается через 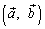 [или
[или 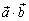 ; или
; или 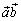 ]. Если φ - угол между векторами
]. Если φ - угол между векторами 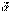 и
и  , то
, то 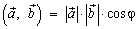 .
.
Скалярное произведение обладает следующими свойствами:
1. 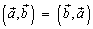 (коммутативность).
(коммутативность).
2. 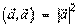 (скалярный квадрат вектора равен квадрату его длины).
(скалярный квадрат вектора равен квадрату его длины).
3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них нулевой.
4. 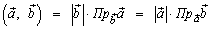 .
.
5. 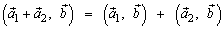 .
.
6. 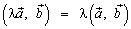 .
.
Векторное произведение
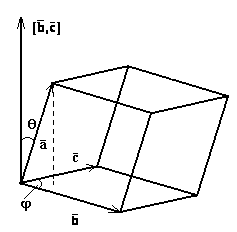
Упорядоченная тройка некомпланарных векторов называется правоориентированной (правой), если после приложения к общему началу из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае упорядоченная тройка некомпланарных векторов называется левоориентированной (левой).
Определение: Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор 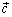 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1. 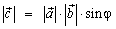 где φ – угол между векторами
где φ – угол между векторами  и
и  ;
;
2. вектор 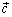 ортогонален вектору
ортогонален вектору  , вектор
, вектор 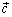 ортогонален вектору
ортогонален вектору  ;
;
3. упорядоченная тройка векторов 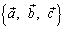 является правой.
является правой.
Если один из векторов нулевой, то векторное произведение есть нулевой вектор.
Векторное произведение вектора  на вектор
на вектор  обозначается
обозначается 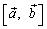 {либо
{либо 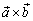 }.
}.
Теорема: Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Теорема: Длина (модуль) векторного произведения двух векторов равняется площади параллелограмма, построенного на этих векторах как на сторонах.
Пример: Если 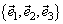 – правый ортонормированный базис, то
– правый ортонормированный базис, то 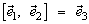 ,
, 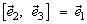 ,
, 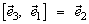 .
.
Пример: Если 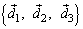 – левый ортонормированный базис, то
– левый ортонормированный базис, то 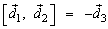 ,
, 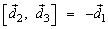 ,
, 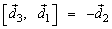 .
.
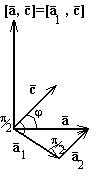
Пример: Пусть, 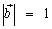 а
а  ортогонален к
ортогонален к  . Тогда
. Тогда 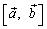 получается из вектора
получается из вектора  поворотом вокруг вектора
поворотом вокруг вектора  на
на 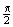 по часовой стрелке (если смотреть из конца вектора
по часовой стрелке (если смотреть из конца вектора  ).
).
Пример: Если дан вектор 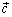 , то каждый вектор можно представить в виде суммы
, то каждый вектор можно представить в виде суммы 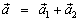 , где
, где 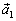 – ортогонален
– ортогонален 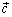 , а
, а 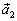 – коллинеарен
– коллинеарен 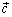 . Легко видеть, что
. Легко видеть, что 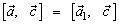 .
.

Действительно, можно заметить, что 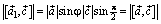 . Вектор
. Вектор 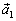 компланарен векторам
компланарен векторам  и
и 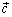 , а потому
, а потому 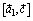 и
и 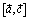 коллинеарны. Легко видеть (рис. 12), что они одинаково направлены.
коллинеарны. Легко видеть (рис. 12), что они одинаково направлены.

Векторное произведение обладает следующими свойствами:
1. 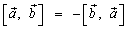 (антикоммутативность);
(антикоммутативность);

Действительно, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей. Точно так же вектор 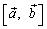 коллинеарен вектору
коллинеарен вектору 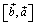 . Однако, переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если
. Однако, переставляя сомножители, мы должны изменить направление произведения, чтобы было выполнено условие 3) определения. Действительно, если  ,
,  ,
, 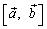 - правая тройка, то
- правая тройка, то  ,
,  ,
, 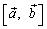 - левая, а
- левая, а  ,
,  ,
, 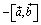 - снова правая тройка.
- снова правая тройка.

2. 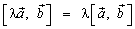 ;
;

Если φ - угол между векторами  и
и  , то
, то 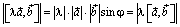 . Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной
. Векторы, стоящие в обеих частях доказываемого равенства, лежат на прямой, перпендикулярной  и
и  . При λ > 0 и вектор
. При λ > 0 и вектор 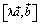 и
и 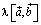 вектор направлены так же, как
вектор направлены так же, как 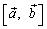 . Если λ < 0, то кратчайший поворот от
. Если λ < 0, то кратчайший поворот от 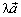 к
к  производится навстречу кратчайшему повороту от
производится навстречу кратчайшему повороту от  к
к  . Поэтому
. Поэтому 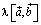 и
и 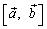 противоположно направлены. Очевидно, что противоположно направлены также и векторы
противоположно направлены. Очевидно, что противоположно направлены также и векторы 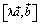 и
и 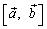 . Таким образом, при λ ≠ 0 векторы
. Таким образом, при λ ≠ 0 векторы 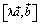 и
и 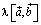 направлены всегда одинаково, и равенство доказано. При λ = 0 равенство очевидно.
направлены всегда одинаково, и равенство доказано. При λ = 0 равенство очевидно.

3. 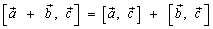 ;
;

Если 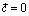 , то доказываемое очевидно. Если
, то доказываемое очевидно. Если 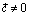 , то разложим
, то разложим  и
и  в суммы
в суммы 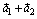 и
и 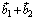 , где
, где 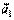 и
и 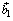 ортогональны
ортогональны 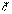 , а
, а 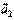 и
и 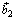 коллинеарны
коллинеарны 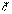 . Поскольку
. Поскольку 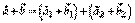 , и вектор
, и вектор 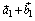 ортогонален
ортогонален 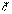 , а
, а 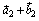 коллинеарен
коллинеарен 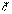 , нам достаточно доказать равенство
, нам достаточно доказать равенство 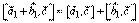 и (в силу свойства 2) даже равенство
и (в силу свойства 2) даже равенство 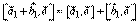 , где
, где 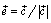 . Длина вектора
. Длина вектора 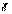 равна 1. Выше, в примере, мы видели, что в этом случае умножение на
равна 1. Выше, в примере, мы видели, что в этом случае умножение на 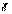 сводится к повороту (ортогонального к
сводится к повороту (ортогонального к 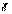 ) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на
) первого сомножителя на угол 90°. Но при повороте параллелограмм, построенный на 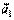 и
и 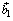 , поворачивается целиком вместе с диагональю. Тем самым равенство доказано.
, поворачивается целиком вместе с диагональю. Тем самым равенство доказано.

4. 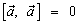 .
.
Пусть в некотором базисе 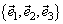 заданы векторы
заданы векторы 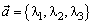 и
и 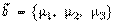 тогда
тогда
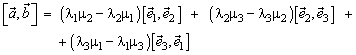
или
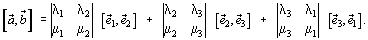

Справедливость теоремы следует из предыдущих формул при учете примеров в начале раздела. Чтобы избежать постоянных замечаний об ориентации базиса, мы будем считать, что базис выбирается всегда правый.

Векторное произведение используется в основном для решения двух задач:
1. Нахождения вектора перпендикулярного плоскости, в которой расположены два заданных вектора.
2.  Вычисление площади S параллелограмма, построенного на векторах
Вычисление площади S параллелограмма, построенного на векторах 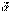 и
и  , как на сторонах. В ортонормированном базисе
, как на сторонах. В ортонормированном базисе
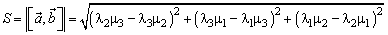
В планиметрии векторное произведение не определено. Но ничто не мешает считать, что изучаемая плоскость помещена в пространство и третий базисный вектор выбран единичным и перпендикулярным плоскости. Тогда векторное произведение имеет одну ненулевую компоненту, а именно третью, и площадь параллелограмма в ортонормированном базисе на плоскости выражается формулой
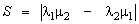 .
.
§ 1.6. Комплексные числа
Комплексным числом называется выражение вида z = a + bi, где a и b – действительные числа, 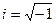 – мнимая единица. Число а называется действительной частью комплексного числа z и обозначается a = Rez, число b – мнимой частью z: b = Imz.
– мнимая единица. Число а называется действительной частью комплексного числа z и обозначается a = Rez, число b – мнимой частью z: b = Imz.
Два комплексных числа z1 = a1 + b1i и z2 = a2 + b2i равны, если a1 = a2 и b1 = b2.
Комплексные числа z = a + bi и z = a – bi называются сопряженными.
Действия над комплексными числами
1. При сложении двух комплексных чисел отдельно складываются их действительные части и мнимые части:
z1 + z2 = (a1 + a2) + (b1 + b2)i. (1)
2. При умножении двух комплексных чисел получается комплексное число:
z1z2 = (a1a2 – b1b2) + (a1b2 + a2b1)i, (2).
3. При делении двух комплексных чисел получается комплексное число:
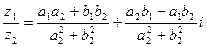 , (3).
, (3).
@ Задача 1. Найти сумму двух комплексных чисел 2 + 3 i и – 4 + 6 i.
Решение: Комплексные числа суммируются по правилу (1): (2 + 3 i) + (– 4 + 6 i) = (2 – 4) + (3 + 6) i = – 2 + 9 i.
@ Задача 2. Найти произведение двух комплексных чисел 2 + 3 i и – 4 + 5i.
Решение: Комплексные числа умножаются по правилу (2):
(2 + 3 i)·(– 4 + 5 i) = (2·(– 4) – 3·5) + (2·5 + 3·(– 4)) i = – 23 – 2 i.
@ Задача 3. Найти частное двух комплексных чисел 2 + 4 i и 1 + i.
Решение: Комплексные числа делятся по правилу (3):
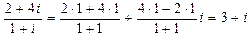 .
.
Тригонометрическая форма комплексного числа
Всякое комплексное число z = a + bi можно изобразить точкой A(a,b) плоскости, такой что a = Rez, а b = Imz. Тогда a и b можно выразить через полярные координаты r и j: a = rcos j, b = rsin j, где r и j называются модулем и аргументом комплексного числа.
Таким образом, комплексное число z = a + bi можно представить в тригонометрической форме
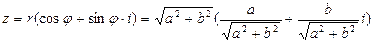 .
.
Экспоненциальной формой комплексного числа называется число 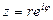 .
.
@ Задача 4. Представить в тригонометрической форме комплексное число 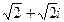 .
.
Решение: Так как 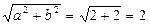 , то комплексное число представляется в тригонометрической форме в виде
, то комплексное число представляется в тригонометрической форме в виде
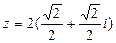 .
.
Корни квадратного и биквадратного уравнений
Корни квадратного уравнения ax 2 + bx + c = 0 с отрицательным дискриминантом D = b 2 – 4ac < 0 являются комплексными числами и находятся по формулам 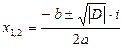 .
.
Корни биквадратного уравнения x 4 + px 2 + q = 0 с отрицательным дискриминантом D = p 2 – 4q < 0 являются комплексными числами и находятся по формулам:
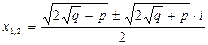 ,
,
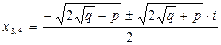 .
.
@ Задача 5. Решить квадратное уравнение x 2 – 4x + 8 = 0.
Решение: Дискриминант квадратного уравнения отрицательный: D = 4 2 – 4×8 = – 16 < 0 и, следовательно, корни квадратного уравнения равны 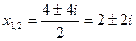 .
.
@ Задача 6. Решить биквадратное уравнение
x 4 – 4x 2 + 16 = 0.
Решение: Дискриминант биквадратного уравнения отрицательный: D = 4 2 – 4×16 = – 48 < 0. Т.к. 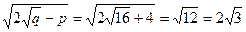 и
и 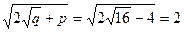 , то
, то 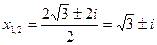 и
и 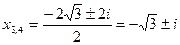 .
.
§ 1.7 Прямые и плоскости в аффинном пространстве. Выпуклые множества и их свойства.
В n -мерном пространстве задаётся упорядоченной системой линейно независимых векторов 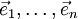 , выходящих из одной точки O. Аффинными координатами точки M называют такие числа xi, что
, выходящих из одной точки O. Аффинными координатами точки M называют такие числа xi, что
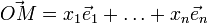
Tочку O и систему векторов 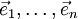 называют репером или аффинным базисом; прямые, проходящие через вектора
называют репером или аффинным базисом; прямые, проходящие через вектора 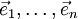 — координатными осями.
— координатными осями.
На аффинной плоскости (n = 2) координату x 1 называют абсциссой, а x 2 – ординатой точки M. В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.

Выпуклые множества и их свойства
Множество 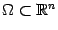 - выпуклое, если вместе с любыми двумя точками
- выпуклое, если вместе с любыми двумя точками 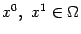 множеству
множеству 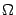 принадлежат все точки
принадлежат все точки 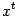 отрезка, соединяющего в пространстве
отрезка, соединяющего в пространстве 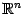 точку
точку 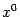 с точкой
с точкой 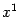 . Заметим, что отрезок, состоящий из точек
. Заметим, что отрезок, состоящий из точек 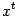 , можно параметризовать следующим образом:
, можно параметризовать следующим образом: 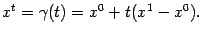 Тогда при
Тогда при 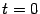 будет получаться точка
будет получаться точка 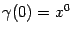 , при
, при 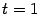 -- точка
-- точка 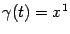 , а при
, а при 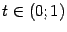 - промежуточные точки отрезка, так что обозначения точек отрезка как
- промежуточные точки отрезка, так что обозначения точек отрезка как 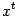 будут согласованы с обозначениями его концов.
будут согласованы с обозначениями его концов.
На следующем рисунке изображены два множества на плоскости 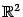 : одно выпуклое, а другое нет.
: одно выпуклое, а другое нет.
Выпуклыми в пространстве 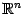 являются, например, такие множества: всё пространство
являются, например, такие множества: всё пространство 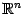 , его положительный октант
, его положительный октант 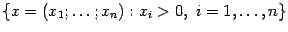 и неотрицательный октант
и неотрицательный октант 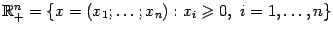 , любой шар, как открытый
, любой шар, как открытый 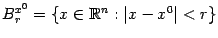 , так и замкнутый
, так и замкнутый 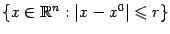 , любая гиперплоскость
, любая гиперплоскость 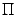 (заданная некоторым уравнением вида
(заданная некоторым уравнением вида 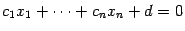 , а также открытое и замкнутое полупространства, заданные, соответственно, условиями
, а также открытое и замкнутое полупространства, заданные, соответственно, условиями 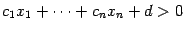 и
и 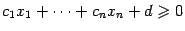 .
.
Теорема 1. Если все множества 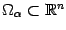 некоторого семейства
некоторого семейства 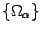 выпуклы, то выпукло и их пересечение
выпуклы, то выпукло и их пересечение
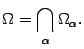
Доказательство. Пусть точки 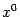 и
и 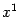 принадлежат
принадлежат 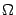 ; тогда обе они принадлежат каждому из множеств
; тогда обе они принадлежат каждому из множеств 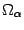 . Значит, если
. Значит, если 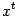 - произвольная точка отрезка, соединяющего
- произвольная точка отрезка, соединяющего 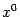 и
и 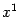 , то она принадлежит
, то она принадлежит 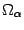 , поскольку
, поскольку 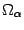 выпукло. Но так как
выпукло. Но так как 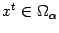 для всех
для всех 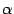 , то
, то 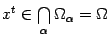 , что и требовалось доказать.
, что и требовалось доказать.
Из этой теоремы следует, например, что прямая в 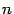 -мерном пространстве (её можно задать как векторным уравнением:
-мерном пространстве (её можно задать как векторным уравнением: 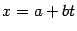 , где
, где 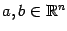 - фиксированные векторы, а
- фиксированные векторы, а 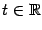 - параметр, так и в виде пересечения гиперплоскостей
- параметр, так и в виде пересечения гиперплоскостей 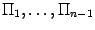 ) является выпуклым множеством. Действительно, каждая гиперплоскость
) является выпуклым множеством. Действительно, каждая гиперплоскость 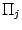 - выпуклое множество.
- выпуклое множество.
Определение: Функция 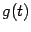 , заданная на отрезке
, заданная на отрезке 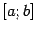 , называется выпуклой (или выпуклой книзу) на этом отрезке, если для всех
, называется выпуклой (или выпуклой книзу) на этом отрезке, если для всех 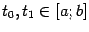 и
и 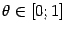 выполняется неравенство
выполняется неравенство
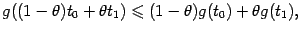
|
и вогнутой (или выпуклой кверху), если выполняется неравенство
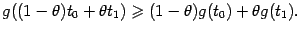
|
(То есть функция 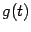 вогнута в том и только том случае, если функция
вогнута в том и только том случае, если функция 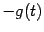 выпукла.)
выпукла.)
В левой части этого неравенства стоит значение функции 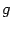 в производной точке
в производной точке
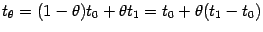
отрезка между 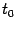 и
и 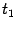 (будем для простоты считать, что
(будем для простоты считать, что 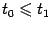 ), а в правой части неравенства - значение линейной функции
), а в правой части неравенства - значение линейной функции 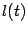 , такой что
, такой что 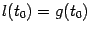 и
и 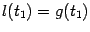
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 371; Нарушение авторских прав?; Мы поможем в написании вашей работы!