
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определителем (детерминантом) квадратной матрицы n-го порядка называется число 1 страница
|
|
|
|
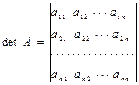 .
.
þ Обозначения: detA, D и | A |.
Строки и столбцы определителя называются рядами.
Определитель второго порядка вычисляется по правилу (1):
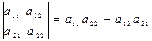 . (1)
. (1)
Определитель третьего порядка вычисляется по правилу (2):
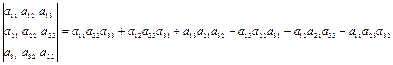 (2).
(2).
Правило вычисления определителя третьего порядка следующее. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах. Со знаком плюс берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали. Со знаком минус берутся произведения, сомножители которых стоят на другой диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).





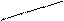

























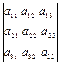
(+) (-)
Рис. 1. Правило вычисления определителя третьего порядка
@ Задача 1. Найти 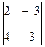 .
.
Решение: Определитель второго порядка вычисляется по правилу (1): detA = 2·3 – (–3)·4=18.
@ Задача 2. Найти 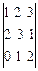 .
.
Решение: Определитель третьего порядка вычисляется по правилу (2):
detA = 1·3·2 + 2·1·0 + 3·2·1 – 3·3·0 – 2·2·2 – 1·1·1 = 3.
Минор и алгебраическое дополнение
Минором mij некоторого элемента aij определителя n–го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя путем вычеркивания i-й строки и j-го столбца, на пересечениях которых находится выбранный элемент.
Например, минором элемента a11 определителя третьего порядка является 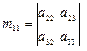 .
.
Алгебраическим дополнением называется Aij = (– 1) i+j mij. Если сумма индексов алгебраического дополнения i + j четное число, то алгебраические дополнения и миноры совпадают: Aij = mij, а если – нечетное число, то они отличаются знаком: Aij = – mij.
Свойства определителей
1. Если какой-то ряд состоит из одних нулей, то определитель равен 0.
2. Определитель не изменится, если его строки заменить столбцами, и наоборот.
3. При перестановке двух параллельных рядов определитель меняет знак.
4. Определитель, имеющий два одинаковых ряда, равен нулю.
5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
6. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух определителей, с соответствующими слагаемыми этой суммы.
7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
8. Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.
Например, определитель третьего порядка равен:
detA = a11A11 + a12A12 + a13A13 = a11m11 – a12m12 + a13m13. (3)
@ Задача 3. Найти 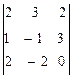 .
.
Решение: Определитель найдем, применяя формулу (3):
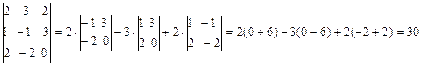
Ранг матрицы
Наибольший порядок отличных от нуля детерминантов (миноров) прямоугольной матрицы m ´ n, называется рангом матрицы r, причем r £ min(m, n). Для квадратной матрицы ранг r £ n.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
@ Задача 4. Найти ранг матрицы 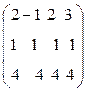 размерности 3´4.
размерности 3´4.
Решение: Ранг матрицы r £ min(3, 4) = 3. Все детерминанты третьего порядка равны нулю, так как две их строки (вторая и третья) одинаковые (отличаются на постоянный множитель). Отличны от нуля только детерминанты второго порядка, поэтому r = 2.
§ 1.4. Обратная матрица
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля: detA ¹ 0. В противном случае матрица называется вырожденной.
Матрица A- 1 называется обратной матрице А, если выполняется условие
A- 1 A = AA- 1 = E.
Только у невырожденных квадратных матриц есть обратные матрицы.
Обратная матрица вычисляется по формуле (detA ¹ 0):
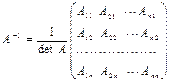 .
.
Для матрицы A второго порядка обратная матрица равна:
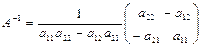 .
.
@ Задача 1. Найти A- 1, если 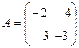 .
.
Решение: 1. Находим определитель матрицы:
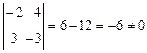 .
.
2. Находим обратную матрицу:
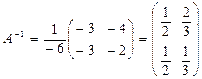 .
.
@ Задача 2. Найти A- 1, если 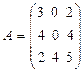 .
.
Решение: 1. Находим определитель матрицы:
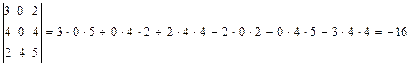 .
.
2. Вычисляем алгебраические дополнения: 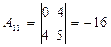 ,
, 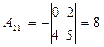 ,
, 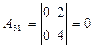 ,
, 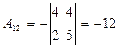 ,
, 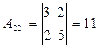 ,
, 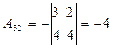 ,
, 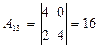 ,
, 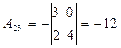 ,
, 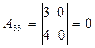 .
.
3. Находим обратную матрицу:
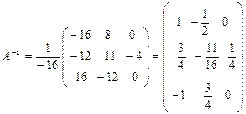 .
.
Свойства обратной матрицы
1. Определитель обратной матрицы A- 1 равен обратной величине определителя матицы A: det(A- 1) = 1/ detA
2. Обратная матрица произведения двух матриц равна произведению их обратных матриц: (A × B) - 1 = B- 1× A- 1
3. При перестановке операций транспонирования и нахождения обратной матрицы результат не изменяется: (A- 1) T = (AT)-1.
Буква T означает операция транспонирования – операция замены строк столбцами и наоборот. В частности, при транспонировании вектор-столбец превращается в вектор-строку.
§ 1.5. Векторы
Понятие вектора
Отрезок на прямой определяется двумя равноправными точками – его концами. Различают также направленный отрезок, т.е. отрезок, относительно концов которого известно какой из них первый (начало), а какой – второй (конец).
Определение: Направленный отрезок (или упорядоченная пара точек) называется вектором.
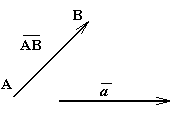
Вектор обычно обозначается символом 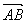 , где А – начало, а В – конец направленного отрезка, либо одной буквой
, где А – начало, а В – конец направленного отрезка, либо одной буквой 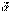 (в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.
(в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.
Расстояние между началом и концом вектора называется его длиной. Для обозначения длины вектора (его абсолютной величины) пользуются символом модуля. Так 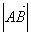 и
и 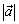 обозначают длины соответствующих векторов.
обозначают длины соответствующих векторов.
Вектор единичной длины называют ортом.
К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Считается, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет обозначать нулевой вектор вещественным числом 0 (нуль).
Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллениарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы.
Векторы называются компланарными, если они лежат, либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.
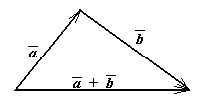
Определение: Два вектора называются равными, если они: 1) коллинеарны; 2) равны по длине; 3) одинаково направлены.
Следствие: Для любого вектора 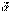 и для любой точки А, существует, и притом единственная, точка B такая, что
и для любой точки А, существует, и притом единственная, точка B такая, что 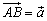 .
.
Мы не будем различать двух равных векторов, имеющих разные точки приложения. Такие векторы называются свободными (в отличие от скользящих и связанных векторов, встречающихся в других науках).
Понятие равенства векторов обладает следующими свойствами:
1. 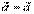 (рефлексивность).
(рефлексивность).
2. Из того, что 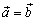 , следует
, следует 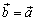 (симметричность).
(симметричность).
3. Из того, что 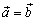 и
и 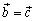 , следует
, следует 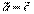 (транзитивность).
(транзитивность).
Операции над векторами
Определение: Суммой 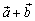 двух векторов и называется вектор, имеющий начало в начале вектора
двух векторов и называется вектор, имеющий начало в начале вектора  , а конец – в конце вектора
, а конец – в конце вектора  , при условии, что вектор
, при условии, что вектор  приложен к концу вектора
приложен к концу вектора  .
.
В соответствии с определением слагаемые  и
и  и их сумма
и их сумма 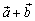 образуют треугольник (рис.3). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
образуют треугольник (рис.3). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
Операция сложения векторов обладает свойствами:
1. 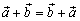 (коммутативность);
(коммутативность);
2. 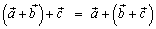 , (ассоциативность);
, (ассоциативность);
3. 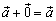 для любого вектора
для любого вектора  (особая роль нулевого вектора);
(особая роль нулевого вектора);
4. для каждого вектора  существует противоположный ему вектор
существует противоположный ему вектор 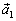 такой, что
такой, что 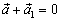 (для получения
(для получения 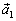 достаточно поменять местами начало и конец вектора
достаточно поменять местами начало и конец вектора  ).
).
Вектор противоположный вектору  обозначают
обозначают 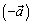 .
.
Определение: Разностью 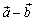 векторов
векторов  и
и  называется сумма вектора
называется сумма вектора  и вектора противоположного вектору
и вектора противоположного вектору  , т.е.
, т.е. 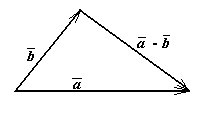
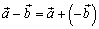 .
.
Разность 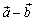 получается из вектора
получается из вектора  сдвигом его начала в конец вектора
сдвигом его начала в конец вектора  , при условии, что векторы
, при условии, что векторы  и
и  имеют общее начало (рис.3). Очевидно, что
имеют общее начало (рис.3). Очевидно, что 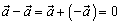 для любого вектора
для любого вектора  .
.
Замечание: Существует еще одно правило сложения векторов, называемое «правилом параллелограмма»: векторы  и
и  прикладываются к общему началу О, и на них строится параллелограмм. Суммой
прикладываются к общему началу О, и на них строится параллелограмм. Суммой 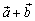 будет вектор
будет вектор 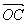 , расположенный на диагонали параллелограмма. Разностью
, расположенный на диагонали параллелограмма. Разностью 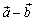 здесь будет вектор
здесь будет вектор 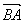 , расположенный на второй диагонали.
, расположенный на второй диагонали.
 Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.
Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.
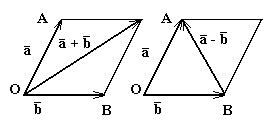
Определение: Произведением 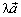 вектора
вектора  на вещественное число λ (скаляр) называется вектор
на вещественное число λ (скаляр) называется вектор  , такой, что 1)
, такой, что 1) 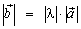 ; 2) вектор
; 2) вектор  коллинеарен вектору
коллинеарен вектору  ; 3) векторы
; 3) векторы  и
и  имеют одинаковое (противоположное) направление, если λ > 0 (λ < 0).
имеют одинаковое (противоположное) направление, если λ > 0 (λ < 0).
Замечание: В случае, когда λ = 0 или 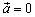 произведение
произведение 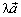 является нулевым вектором.
является нулевым вектором.
Операция умножения вектора на число обладает следующими свойствами:
1. 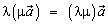 (ассоциативное свойство сомножителей);
(ассоциативное свойство сомножителей);

Действительно, заметим, что векторы, стоящие обеих частях равенства, имеют одну и ту же длину 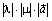 . Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением
. Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением  , если λ и μ одного знака, и противоположно направлению
, если λ и μ одного знака, и противоположно направлению  , если λ и μ имеют разные знаки. Если же λ или μ равны нулю, то обе части равенства равны нулю. Свойство доказано.
, если λ и μ имеют разные знаки. Если же λ или μ равны нулю, то обе части равенства равны нулю. Свойство доказано.

2. 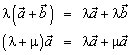 (свойства дистрибутивности).
(свойства дистрибутивности).
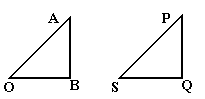

Построим треугольник OAB где 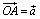 и
и 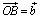 . Построим далее треугольник SPQ, где
. Построим далее треугольник SPQ, где 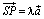 и
и 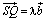 . Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что
. Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что 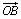 и
и 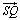 одинаково направлены, если λ > 0. Отсюда следует, что
одинаково направлены, если λ > 0. Отсюда следует, что 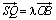 . Но
. Но 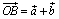 и
и 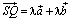 , а отсюда вытекает первое свойство дистрибутивности.
, а отсюда вытекает первое свойство дистрибутивности.
Очевидно, что векторы стоящие в обеих частях второго свойства дистрибутивности коллинеарны. Допустим сначала, что знаки λ и μ одинаковы. Тогда векторы 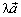 и
и 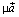 направлены одинаково и длина их суммы равна сумме их длин, т. е.
направлены одинаково и длина их суммы равна сумме их длин, т. е. 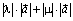 . Но
. Но 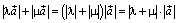 и следовательно, в этом случае векторы
и следовательно, в этом случае векторы 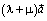 и
и 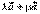 равны по длине. Направление их совпадает с направлением вектора
равны по длине. Направление их совпадает с направлением вектора 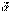 , если общий знак λ и μ положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки λ и μ различны, и для определенности будем считать |λ| > |μ|. В этом случае длина суммы равна разности длин, точнее
, если общий знак λ и μ положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки λ и μ различны, и для определенности будем считать |λ| > |μ|. В этом случае длина суммы равна разности длин, точнее 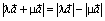 . Но
. Но 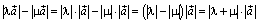 . Следовательно, и в этом случае длина вектора
. Следовательно, и в этом случае длина вектора 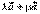 равна длине вектора
равна длине вектора 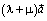 . Очевидно, что оба эти вектора направлены так же, как
. Очевидно, что оба эти вектора направлены так же, как 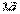 . Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор
. Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор 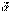 или оба скаляра одновременно.
или оба скаляра одновременно.

Теорема: Если вектор  коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 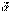 , то существует вещественное число λ такое, что
, то существует вещественное число λ такое, что  = λ
= λ 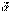 .
.
Проекция вектора
Под углом между векторами понимается угол между векторами равными данным и имеющими общее начало. Если направление отсчета угла не указано, то углом между векторами считается тот из углов, который не превосходит π. Если один из векторов нулевой то угол считается равным нулю. Если угол между векторами прямой то векторы называются ортогональными.
Определение: Ортогональной проекцией 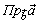 вектора
вектора  на направление вектора
на направление вектора  называется скалярная величина
называется скалярная величина 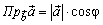 , φ – угол между векторами.
, φ – угол между векторами.
Модуль этой скалярной величины равен длине отрезка OA0.
Если угол φ острый проекция является положительной величиной, если угол φ тупой – проекция отрицательна, если угол φ прямой – проекция равна нулю.
При ортогональной проекции угол между отрезками OA0 и AA0 прямой. Существуют проекции, у которых этот угол отличен от прямого.
Проекции векторов обладают следующими свойствами:
1. 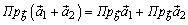 (проекция суммы равна сумме проекций);
(проекция суммы равна сумме проекций);
2. 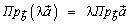 (проекция произведения вектора на число равна произведению проекции вектора на число).
(проекция произведения вектора на число равна произведению проекции вектора на число).
Базис называется ортогональным, если его векторы попарно ортогональны.
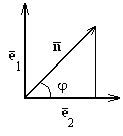
Ортогональный базис называется ортонормированным, если его векторы по длине равны единице. Для ортонормированного базиса в пространстве часто используют обозначения 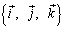 .
.
Теорема: В ортонормированном базисе координаты векторов есть соответствующие ортогональные проекции этого вектора на направления координатных векторов.
Пример: Пусть вектор 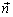 единичной длины
единичной длины 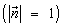 образует с вектором
образует с вектором 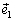 ортонормированного базиса
ортонормированного базиса 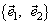 на плоскости угол φ, тогда
на плоскости угол φ, тогда 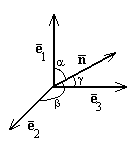
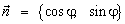 .
.
Пример: Пусть вектор 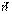 единичной длины
единичной длины 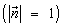 образует с векторами
образует с векторами 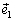 ,
, 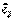 и
и 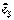 ортонормированного базиса в пространстве углы α, β, γ, соответственно (рис. 5), тогда
ортонормированного базиса в пространстве углы α, β, γ, соответственно (рис. 5), тогда 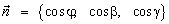 . Причем
. Причем 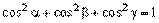 . Величины cosα, cosβ, cosγ называются направляющими косинусами вектора
. Величины cosα, cosβ, cosγ называются направляющими косинусами вектора 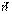
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 689; Нарушение авторских прав?; Мы поможем в написании вашей работы!