Тема № 2 Системы линейных алгебраических уравнений

Прямая проходит через точки О(0;0) и В(5;-15). Тогда ее угловой коэффициент равен...

Расстояние между точками А(-1;1) и В(k;-3) равно 5 при k равном...

Решить систему линейных уравнений методом Гаусса. Найти Х1; Х2; Х3

Обратной матрицей обладают

£ все матрицы;

£ все квадратные матрицы;

£ невырожденные квадратные матрицы;

£ вырожденные квадратные матрицы.

£ X1=83; X2=-20; X3=-30

£ X1=47; X2=-36; X3=-17

£ X1=92; X2=-40; X3=-10

£ X1=54; X2=-14; X3=-28

£ -1

£ 4

£ 2

£ 8

£5

£ -3

£ 3

£ -5

36.Прямая проходит через точки О(0;0) и В(25;15). Тогда ее угловой коэффициент равен…

£3/5

£ 5/3

£ 5/3

£ -3/5

§ 2.1. Система линейных алгебраических уравнений, содержащей n уравнений и n неизвестных

Системой линейных алгебраических уравнений, содержащей n уравнений и n неизвестных, называется система вида

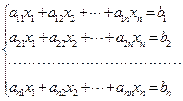(1),

где a_ij, i = 1,2,… n; j = 1,2,…n - коэффициенты системы, b_i, i = 1,2,… n - свободные члены, x_i, i = 1,2,… n - неизвестные, подлежащие нахождению.

Более удобной формой записи системы линейных уравнений (1) является матричная форма

A·X = B, (2)

где А - квадратная матрица n -го порядка, X – вектор столбец из неизвестных x_i, i = 1,2,… n, B – вектор-столбец из свободных членов b_i, i = 1,2,… n.

Система уравнений (1) имеет единственное решение, если матрица А невырожденная, т.е. если определитель матрицы А отличен от нуля: D ¹ 0. Решение матричного уравнения (2) находится следующим образом:

A^{- 1} AX = A^{- 1} B, EX = A^{- 1} B, X = A^{- 1} B. (3)

Решение X = A^{- 1} B справедливо не только для векторов столбцов X и B, но и для произвольных матриц X и B, удовлетворяющих уравнению (2).

Формула Крамера

Решения системы линейных уравнений (1) определяются формулой Крамера

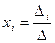, i= 1,2··· n, (4)

где D _i получается из определителя D путем замены i -го столбца свободными членами b_i. Формула Крамера получается из решения системы X = A^{- 1} B. На самом деле, это решение в виде системы записывается как:

.

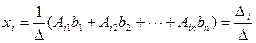@ Задача 1. Найти решение системы .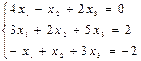

Решение: Решение системы уравнений находится с помощью формулы Крамера.

1. Находим определители , , , ;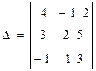

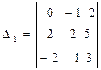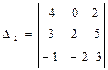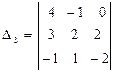D = 4×2×3 + (–1)×5×(–1) + 2×3×1 – 2×2×(–1) – (–1)×3×3 – 4×5×1 = 28;

D₁ = 0×2×3 + (–1)×5×(–2) + 2×2×1 – 2×2×(–2) – (–1)×2×3 – 0×5×1 = 28;

D₂ = 4×2×3 + 0×5×(–1) + 2×3×(–2) – 2×2×(–1) – 0×3×3 – 4×5×(–2) = 56;

D₃ = 4×2×(–2) + (–1)×2×(–1) + 0×3×1 – 0×2×(–1) – (–1)×3×(–2) – 4×2×1 = – 28.

2. Решение системы равно: , , .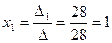

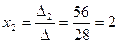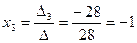Метод последовательных исключений неизвестных (метод Гаусса)

С помощью коэффициентов и свободных членов составляется расширенная матрица

,

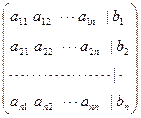над строками которой можно произвести следующие элементарные преобразования. Разрешается изменить порядок строк; прибавлять к элементам произвольной строки элементы другой строки, умноженное на любое отличное от нуля число. При этом нужно стараться свести расширенную матрицу к «треугольному» виду, т.е. к виду, когда все элементы ниже (или выше) главной диагонали равны нулю. Из полученной расширенной матрицы решение находится непосредственно:

.

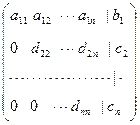т.е. 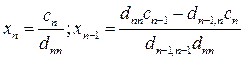и т.д.

@ Задача 2. Решить систему уравнений: .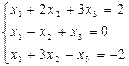

Решение: Составляем расширенную матрицу и сводим ее к «треугольному» виду:

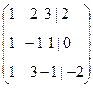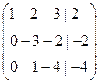Þ Þ .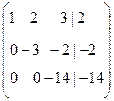

После этого нетрудно найти решения:

– 14x₃ = – 14: x₃ = 1; – 3x₂ – 2x₃ = – 2; x₂ = 0;

x₁ + 2x₂ + 3x₃ = 2; x ₁ = – 1.

§ 2.2. Система линейных алгебраических уравнений, содержащая

m уравнений и n неизвестных

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

.

Система уравнений называется совместной, если она имеет, хотя бы одно решение, и несовместной, если не имеет ни одного решения. Ответ на совместность системы дает теорема Кронекера-Капелли.

Дата добавления: 2014-12-27