Метод деления дробных

Беззнаковое деление

Семантика

Умножение знаковое в С51

Test на семантику операции умножения и знак порта

#include <reg51.h> //заголовочный файл с адресами SFR-регистров

char x=0x80; // <0

unsigned z=0x80; //>0

int y;

main()

{

y=x*P1; //y=0xС00 <0 P1=0x80 >0 и char x<0

y=z*P1; //y=0x4000 >0 P1=0x80 >0 и unsigned char z>0

}

Произведение s=x*y

1) x>0, y>0 s= x*y

2) x<o,y<0 s=(1-x)(1-y)=1-x-y+xy -требуется коррекция +x+y

преобразование сомножителей

(1-x)=(1-1.x)

(1-y)=(1-1.y)

(1-1.x) (1-1.y)= 1-x-y +(1+x)(1+y)=1-x-y+1+x+y+xy=xy

2 – за пределами формата

3) x<o,y>0 s=(1-x)y= y-xy требуется коррекция –y

(1-1.x)y = y –y –xy =1-xy

4) y<o,x>0 s=(1-y)x= x-xy коррекция –x

(1-1.y)x = x –x –xy =1-xy

8*8 в доп.кодах выполняется после преобразования сомножителей

как 16*16à16

int y=x*P1; //v<0, x<0. P1>0

в Реассемблере

MOV R5, P1(0x90);ввод беззнакового P1и выравнивание форматов 16*16-->16

MOV R4,#0x00; R4.R5= 0.P1

MOV R7,x; преобразование x в R6.R7

MOV A,R7

RLC A

SUBB A,ACC; преобразование к специальному формату (-)множимого x

MOV R6,A

LCALL C?IMUL;стандартная подпрограмма беззнакового умножения

; r4r5 * r6.r7 à r6.r7

MOV y(0x0B),R6

MOV 0x0C,R7 //произведение а рабочих регистрах R6.R7

Прямое деление целых чисел затруднительно, так как требуется нормализация – приведение делителя к делимому, где делимое меньше делителя. Нормализация, естественно, предполагается при выполнении деления с дробными, где для обратной к умножению операции деления должно соблюдаться всегда условие произведение(делимое) меньше сомножителя (делителя). Если умножение выполняется по методу умножения дробных чисел, то естественно и деление рассматривать как обратное действие для дробных чисел.

Если произведение S=A*B дробное, то частное B=S/A дробное при условии, что S<A (правило деления в арифметике дробных чисел).

Если на последнем шаге вычисления (формула 2.1) дробного произведения получим

S=A*B=S_n=2^-1(S_n-1+Ab₁), то b₁ =1 при условии, что S_n-1 = 2Sn-A >=0, иначе b₁ =0. и так далее на каждом шаге b_i =1, если S_n-i = 2S_n-i-1-A >=0, иначе b_i =0.

Изменяя нумерацию остатков при выполнении условия S<A, приходим к следующей рекуррентной формуле деления

(2.6) S_i+1= 2S_i-A и b_i=1, если 2S_i-A >=0, где S₀=S-делимое

S_i+1= 2S_i и b_i=0, если 2S_i-A <0

В схеме вычислений на Си форматы операндов выровнены для выполнения вычитания.

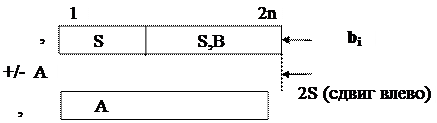Рис.2.5. Схема деления в Си без восстановления остатка.

Регистр S.B совмещает младшие разряды делимого при сдвиге и разряды частного.

В программе на языке С необходимо контролировать знак остатка в явном виде, при этом сужается диапазон значений делимого и делителя.для беззнаковых(положительных) чисел.

Main()

{ Int S=P1<<8;

Int A=P2<<8;

For (char i=0; i<8; i++;)

P3=S= ((S<<1)-A)>=0)? (S<<1)-A +1: S<<1;

}

В Ассемблере можно контролировать как бит признака С, так и старшие биты операндов, что позволяет работать без знаков в полных форматах (n-разрядный делитель и 2n-разрядное делимое) значений операндов.

Отрицательный остаток не сохраняется

C

Рис. 2.6. Схема деления в Ассемблере.

Особенностью целых арифметических операций является абсолютная погрешность, фиксированная единицей, свойственная целым числам, но при сохранении этой точности изменяются диапазоны и форматы данных в процессе вычислений. Таким образом, подразумевается 2n-разрядное произведение n-разрядных целых и делимое при n-разрядном делителе

Знаковые числа преобразуются в прямой код и деление выполняется с модулями – результат преобразуется в знаковое число.

3.2.4. И звлечение квадратного корня

Обычно как функция включается в стандартную библиотеку с плавающей точкой. Однако известны случаи, где в систему команд ЭВМ включается специальная команда быстрого вычисления квадратного корня

Формат подкоренного числа 16 бит. Результат занимает 8-разрядный формат

Алгоритм извлечения для дробного двоичного числа 0.B=√0.S₀.

Пусть i+1-ое приближенное двоичное значение корня x_i+1= x_i b_i+1 и b_i+1 -младшая двоичная цифра в этом приближении, S₀-дробное подкоренное значение не равно 0, x₀=0-начальное -целое значение дробного корня, b_i+1- текущая двоичная цифра корня.

На первом шаге S₀>=(x₀ +0.b₁)² =(x₀ +0.1)² =x₀² +x₀+0.01, x₁ =0.b₁ и b₁=1-старшая цифра дробного корня, если

S₁=S₀-0.01 >=0

Пусть b₁=1 и S₁>=0, тогда на втором шаге сдвинем остаток S₁ на 2 разряда влево и значение корня x₁ на один разряд влево – обозначим новое значение этого остатка Q₁.S₁, где Q₁-целая часть и S₁-дробная часть и x₁= b₁.

Предположим x₂= b₁,b₂

Q₁.S₁>=(x₁ + 0.b₂)² = x₁² +x₁+0.01 и b₂=1, если

Q₂.S₂=4Q₁.S₁-x₁.01=x₁² >=0

Пусть b₂=1 и Q2.S₂>=0, тогда на третьем шаге сдвинем остаток на 2 разряда влево – получим Q₃.S₃, где Q₃-целая часть и S₃-дробная часть и корень сдвинем на один разряд влево x₂= b₁,b₂ и получим x₃= b₁b₂,b₃

Q₃.S₃>=(x₂ + 0.b₃)² = x₂² +x₂+0.01 и b₃=1, если

Q₃.S₃=4Q₂.S₂-x₂.01=x₂² >=0

Рекуррентные формулы для вычисления корня методом “цифра за цифрой” без восстановления остатка

(2.7) Q_i+1.S_i+1=4Q_i.S_i-x_i.01=x_i² и b_i+1=1, если 4Q_i.S_i-x_i.01 >=0

Q_i+1.S_i+1=4Q_i.S_i=x_i² и b_i+1=0, если 4Q_i.S_i-x_i.01 <0

Рис. 2.6. Схема извлечения корня в Ассемблере без восстановления остатка.

Задание:

Разработать и отладить программы в С51 и на Ассемблере а51. Сравнить объем программ. Представить алгоритмы как рекурсивные функции – подготовить программы и сравнить с циклическими.

.

Дата добавления: 2014-12-27