Связь между напряженностью электрического поля и потенциалом

Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины j. Между этими величинами должна существовать связь. Так как Е пропорциональна силе, действующей на заряд, а j – потенциальной энергии заряда, понятно,.что эта связь должна быть аналогична связи между потенциальной энергией и силой. Работа сил поля над зарядом q на отрезке пути d l представима, с одной стороны, как qE_l d l, с другой стороны – как убыль потенциальной энергии заряда 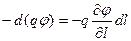. Тогда

откуда

ИЛ)

где через l обозначено произвольно выбранное направление в пространстве. В частности,

Щ-4

откуда

Выражение в скобках называется градиентом скаляра j. Обозначается как grad j или с использованием оператора набла: Ñ j. Используя обозначение градиента, можно написать:

E = – grad j AL3)

Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком. Градиент некоторой скалярной функции j (х, у, z) есть векторная величина, обладающая следующими свойствами.

Направление градиента совпадает с направлением n, в котором при смещении из данной точки функция j, возрастая по величине, изменяется с наибольшей скоростью. Величина производной по этому направлению дает модуль градиента. Частные производные - 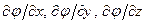представляют собой проекции градиента на координатные оси х, у, z. Аналогично производная 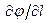, взятая по произвольному направлению l, будет проекцией градиента на это направление. Проекция градиента на перпендикулярное к n направление t, очевидно, равна нулю: .

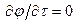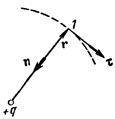Рис. 20.

Проверим соотношение между напряженностью поля и потенциалом на примере поля точечного заряда. Потенциал этого поля выражается функцией [см. A0.3)]

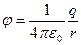
Рассмотрим точку поля 1, положение которой определяется радиусом - вектором r (рис. 20 выполнен в предположении, что q положителен). При смещении из этой точки в разных направлениях на одинаковый по величине малый отрезок d l наибольшее положительное приращение j получается для направления от точки 1 к заряду q, если заряд положителен, и для направления от заряда q к точке 1, если заряд отрицателен. Следовательно, направление градиента n может быть представлено в виде

A1.4)

где знак «–» соответствует случаю положительного заряда, знак «+»– отрицательного. Проекция grad j на направление r равна

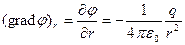Ъ\

Знак «–» в этом выражении указывает на то, что grad j в случае положительного заряда имеет направление, противоположное r, а в случае отрицательного заряда – совпадающее с r. Модуль grad j, очевидно, равен модулю выражения (П.5). Поэтому, с учетом A1.4), получим:

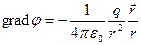
Пользуясь A1.3), для напряженности поля точечного заряда известную формулу E.3).

Можно рассмотреть обратную задачу, т. е. по заданным значениям Е в каждой точке найти разность потенциалов между двумя произвольными точками поля. Учтем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть вычислена как

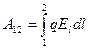
Та же работа может быть представлена в виде

A ₁₂ = q (j ₁ - j ₂)

Отсюда получаем

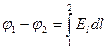A1.7)

Интеграл в правой части можно брать по любой линии, соединяющей точки 1 и 2, так как работа сил поля не зависит от пути. Для обхода по замкнутому контуру j ₁ = j ₂ и формула A1.7) переходит в соотношение (9.2).

Используем формулу A1.7) для вычисления разности потенциалов между двумя бесконечными разноименно заряженными плоскостями. Напряженность поля между

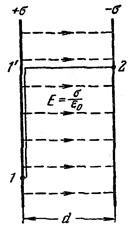Рис. 21.

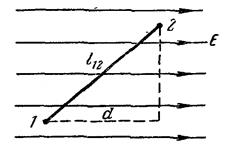Рис. 22.

плоскостями равна s/e₀ и направлена перпендикулярно к плоскостям. Соединим точки 1 и 2, взятые произвольным образом на разных плоскостях, линией 1 – 1'– 2, как показано на рис. 22.

Согласно формуле A1.7)

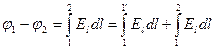
На участке 1 – 1' E_l = 0; поэтому первое слагаемое в правой части равно нулю (отсюда следует, что потенциал точек 1 и 1' один и тот же). На участке 1' – 2 E_l = Е = const, следовательно,

где d – расстояние между плоскостями. Таким образом,

j ₁ - j ₂ = Ed A1.8)

Очевидно, что этот результат справедлив для разности потенциалов между двумя точками, взятыми в однородном поле напряженности Е, причем под d следует понимать в этом случае проекцию расстояния 12 между точками 1 и 2 на направление вектора Е (рис. 22).

Дата добавления: 2015-04-24