Поляризация и плотность связанных зарядов

Рис 31.

Рассмотрим внутри диэлектрика две одинаковые по величине воображаемые площадки S ₁ и S ₂. Площадки предполагаем перпендикулярными к Е и отстоящими друг от друга на D x (рис. 31). До включения поля суммарный заряд, заключенный в цилиндрическом объеме с основанием S и высотой D x, равен нулю (диэлектрик всюду нейтрален). При включении поля через площадку S ₁ входит внутрь цилиндра положительный заряд q == P ₁ S (см. (15.4)), P ₁ – модуль вектора Р в сечении S ₁.

Одновременно через S ₂ выходит из цилиндра положительный заряд q == P ₂ S (Р2 – модуль вектора Р в сечении S ₂). В результате в рассматриваемом объеме оказывается избыточный связанный положительный заряд

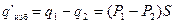(15.5)

Если диэлектрик поляризован однородно (Р = const), то P ₁ = Р ₂ и выражение (15.5) обращается в нуль. Следовательно, в однородно поляризованном диэлектрике избыточные объемные связанные заряды не возникают. Однако, если диэлектрик по какой-либо причине поляризуется неоднородно, равенство P ₁ = Р ₂ уже не выполняется. Причинами неоднородной поляризации могут быть как неоднородности самого диэлектрика, так и неоднородности поля Е (правда, не всякие, а лишь такие, какие вызваны присутствием свободных зарядов в месте неоднородности).

Предположим, что степень поляризации диэлектрика изменяется только в направлении оси х, совпадающей с направлением Е (рис. 31). Тогда P ₁ – Р ₂ представляет собой приращение D Р, которое получает модуль вектора Р при смещении вдоль оси х на Dх. Поскольку DР ¹ 0, в цилиндрическом объеме величиной S D x возникает избыточный заряд, равный согласно (15.5)

Разделив этот заряд на объем цилиндра S D x, получим объемную плотность связанных зарядов в сечении с координатой х (D x полагаем малым):

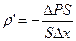
Сократив на S и устремив D x к нулю, придем к формуле

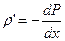(15.6)

В общем случае, когда Р не совпадает по направлению с осью х и зависит не только от х, но и от координат y и z, для r ' получается формула

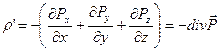(15.7)

В случае, для которого мы получили формулу (15.6), Р _х = Р, Р _y = Р _z =0, так что (15.6) есть не что иное, как (15.7), написанная для рассмотренного нами частного случая.

Полученное нами соотношение оказывается справедливым и для диэлектриков с полярными молекулами.

Из выражения (15.5) для избыточного связанного заряда, заключенного в рассматриваемом объеме, вытекает еще одно важное соотношение. Найдем поток вектора Р через поверхность цилиндра, изображенного на рис. 31. Поток через боковую поверхность равен нулю, так как вектор Р касателен к этой поверхности. Нормальная составляющая Р для площадки S ₂ равна модулю вектора Р в сечении 2, т. е. Р ₂. Поэтому для потока через S ₂ получается значение P ₂ S (напомним, что площадь площадок S ₁ и S ₂ одинакова и равна S). Нормальная составляющая Р для площадки S ₁ равна – P ₁ (направления внешней нормали к S ₁ и вектора Р противоположны), так что соответствующий поток равен – P ₁ S. Таким образом, полный поток вектора Р через поверхность цилиндра равен

Ф _p = P ₂ S – P ₁ S = (Р ₂ – P ₁) S.

Сопоставив полученное нами выражение с правой частью формулы (15.5), приходим к соотношению между избыточным связанным зарядом, заключенным внутри цилиндра, и потоком вектора Р через поверхность цилиндра:

(15.8)

Избыточный заряд, заключенный в некотором объеме, равен алгебраической сумме находящихся в этом объеме связанных зарядов: .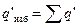

Поэтому (15.8) можно записать в виде

(15.9)

Можно доказать, что формула (15.9) остается справедливой и в самом общем случае, т. е. для поверхности любой формы, при произвольной зависимости вектора Р от координат х, у, z, а также для диэлектриков как с неполярными, так и с полярными молекулами.

Теперь выясним, что происходит на поверхности поляризованного диэлектрика. Предположим вначале, что внешняя плоская грань диэлектрика перпендикулярна к вектору Р (рис. 32,а). При включении поля все отрицательные заряды сместятся относительно положительных зарядов влево (против Р) на одинаковую величину l (соответствующую l ₁+ l ₂ на рис. 30). В результате в поверхностном слое толщины l останутся только положительные заряды, дающие в сумме q ’_изб = enSl (на противоположной грани образуется такой же по величине отрицательный заряд). Разделив q ’_изб на S, получим поверхностную плотность связанного заряда: s ’ = enl. Но eln, как мы установили выше, есть модуль вектора поляризации Р, поэтому можно написать, что

s ’ = P (15.10)

Перейдем к случаю, когда нормаль n к внешней плоской грани диэлектрика образует с вектором Р произвольный угол a (рис. 32,6). В этом случае свободен от отрицательных

Рис. 32.

зарядов объем косого цилиндра, равный Sl cos a. Содержащийся в нем избыточный заряд равен q ’_изб = enSl cos a. Разделив этот заряд на S и учтя, что eln = Р, получим

s ’ = P cos a = P _n (15.11)

где P _n – проекция вектора Р на внешнюю нормаль к поверхности диэлектрика. При a = 0 проекция P _n равна Р, и мы приходим к формуле (15.10).

Формула (15.11) дает не только величину, но и знак поверхностного связанного заряда. В тех точках поверхности, где угол между внешней нормалью n и вектором Р острый, P _n > 0 и s ’ положительна.. В тех точках, где n и Р образуют тупой угол, P _n < 0 и s ' отрицательна. Выразив согласно (15.2) Р через k и Е, приходим к формуле

s ’ = ke ₀ E _n (15.12)

где E _n – нормальная составляющая напряженности поля внутри диэлектрика. В соответствии с (15.12) в тех местах, где линии напряженности выходят из диэлектрика (E _n > 0), на поверхности выступают положительные связанные заряды, там же, где линии напряженности входят в диэлектрик (E _n <0), появляются отрицательные поверхностные заряды.

Формулы (15.11) и (15.12) справедливы и в самом общем случае, когда неоднородный диэлектрик произвольной формы находится в неоднородном электрическом поле. Под P _n и E _n в этом случае нужно понимать нормальную составляющую соответствующего вектора, взятую в непосредственной близости к тому элементу поверхности, для которого определяется s ’.

Дата добавления: 2015-04-24