Преломление линий электрического смещения

Поле вектора D можно изобразить с помощью линий электрического смещения (мы будем для краткости называть их линиями смещения), направление и густота которых определяются точно так же, как и для линий вектора Е.

Поместим в однородное поле Е ₀ две сложенные вместе плоскопараллельные однородные пластины из разных диэлектриков (рис. 37). При разных e ₁ и e ₂ плотности зарядов s '₁ и s '₂ также будут различными. Следовательно, на поверхности, по которой соприкасаются

Рис. 37.

пластины, возникнет избыточный связанный заряд q '_изб. Однако, как мы знаем, линии вектора D могут начинаться и заканчиваться только на свободных зарядах. Поэтому линии смещения пройдут через поверхность раздела двух диэлектриков, не прерываясь. Они лишь, как мы покажем ниже, претерпевают на этой поверхности излом.

Найдем соотношения между нормальными, а также между тангенциальными (по отношению к поверхности раздела) составляющими векторов D и Е в первом и во втором диэлектриках.

Рассмотрим воображаемый цилиндр высоты h, основания которого S ₁ и S ₂ расположены по разные стороны поверхности раздела (рис. 37,а). Применим к этому цилиндру теорему Гаусса. Внутри цилиндра имеются лишь связанные заряды, свободных зарядов по предположению там нет. Поэтому правая часть в формуле (16.5 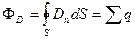) обращается в нуль. Потоком D через боковую поверхность цилиндра можно пренебречь, так как h мы устремим к нулю. Поток через верхнее основание цилиндра равен D _ln S ₁, где D _ln – нормальная составляющая вектора D в первом диэлектрике в непосредственной близости к поверхности раздела. Аналогично поток через нижнее основание есть D _2n S ₂, где D _2n – нормальная составляющая вектора D во втором диэлектрике также в непосредственной близости к поверхности раздела диэлектриков. Сложив эти два потока, мы получим полный поток, который по условию должен быть равен нулю:

Ф _D = D _ln S ₁ + D _2n S ₂ = (D _ln + D _2n) S = 0.

Отсюда следует, что D _ln = – D _2n. Знаки составляющих оказались различными вследствие того, что нормали n ₁ и n ₂ к основаниям цилиндра имеют противоположные направления. Если проектировать D _ln и D _2n на одну и ту же нормаль, то получится, что

D _ln = D _2n (17.1)

Заменив согласно (16.9 D = e ₀ e Е) составляющие D соответствующими составляющими вектора Е, умноженными на e₀e, получим соотношение

e₀e₁ Е _ln = e₀e₂ Е _2n

из которого следует, что

(17-2)

Теперь обратимся к тангенциальным составляющим векторов Е и D. Согласно формуле (16.1) Е = Е ₀ + Е '.

Вектор Е ₀ в обоих диэлектриках по предположению одинаков. Векторы Е ', как видно из рис. 37, б, направлены по нормали к поверхности раздела, вследствие чего оказывают влияние только на нормальные составляющие вектора Е. Отсюда заключаем, что тангенциальные составляющие вектора Е в обоих диэлектриках должны быть одинаковыми:

Е _1t = Е _2t (17.3)

Заменив согласно (16.9 D = e ₀ e Е) составляющие Е соответствующими составляющими вектора D, деленными на e₀e, получим соотношение

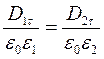
из которого следует, что

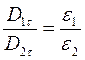(17.4)

Резюмируя, можно сказать, что при переходе через границу раздела двух диэлектриков нормальная составляющая вектора D и тангенциальная составляющая вектора Е изменяются

Рис 38.

непрерывно. Тангенциальная же составляющая вектора D и нормальная составляющая вектора Е при переходе через границу раздела претерпевают разрыв.

На рис. 38 показаны линии смещения для тех же пластин, что и на рис. 37. Вне пластин D = e₀ Е ₀. На границах диэлектриков линии терпят излом (преломляются), вследствие чего угол a между нормалью к поверхности раздела и линией D изменяется. Из рисунка следует, что

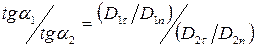
откуда с учетом формул (17.1) и (17.4) получается закон преломления линий электрического смещения

(17-5)

При переходе в диэлектрик с меньшей e угол, образуемый линиями смещения с нормалью, уменьшается, следовательно, линии располагаются реже; при переходе в диэлектрик с большей e линии смещения, напротив, сгущаются.

Дата добавления: 2015-04-24