Взаимодействие токов. 5 страница

Пусть контур 2 неподвижен, и ток индуцируется в нем путем изменения тока i ₁ в первом контуре. В этом случае индуцируется ток i ₂ такого направления, что создаваемый им собственный магнитный поток стремится ослабить изменения внешнего потока, приведшие к появлению индукционного тока. При увеличении i ₁ т. е. возрастании внешнего магнитного потока, направленного вправо, возникнет ток i ₂”, создающий поток, направленный влево. При уменьшении i ₁ возникает ток I, собственный магнитный поток которого направлен так же, как и внешний поток, и, следовательно, стремится поддержать внешний поток неизменным.

Электродвижущая сила индукции.

Для создания тока в цепи необходимо наличие э. д. с. Поэтому явление электромагнитной индукции свидетельствует о том, что при изменениях магнитного потока Ф в контуре возникает электродвижущая сила индукции e _i.

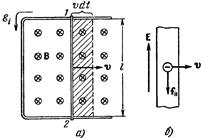Рис. 106.

Чтобы выяснить связь между e _i и скоростью изменения Ф, рассмотрим следующий пример. Возьмем контур, участок которого 1–2 длины l может перемещаться без нарушения контакта с остальной частью контура (рис. 106,а). Поместим его в однородное магнитное иоле, перпендикулярное к плоскости контура (это поле изображено на рисунке кружками с крестиками – вектop В направлен от нас за чертеж). Приведем подвижную часть контура в движение со скоростью v. С той же скоростью станут перемещаться относительно поля и носители заряда в проводнике – электроны (рис. 106,6).

В результате на каждый электрон начнет действовать сила Лоренца f _ïï равная по модулю

f _ïï = qvB (56.1)

(индекс «_||» указывает на то, что сила направлена вдоль провода).

Действие этой силы эквивалентно действию электрической силы, обусловленной полем напряженности

E = vB

имеющим направление, указанное на рис. 106, б. Это поле неэлектростатического происхождения. Его циркуляция по контуру дает величину э. д. с, индуцируемой в контуре:

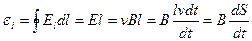(56.2)

где d S = lv d t – приращение площади контура за время d t (это приращение равно заштрихованной площади на рис. 106, а). При вычислении циркуляции мы учли, что e _i отлична от нуля лишь на участке длины l, причем на этом участке всюду E_l = Е.

Произведение В d S дает d Ф – приращение потока магнитной индукции через контур. Следовательно, мы пришли к выводу, что э. д. с. индукции e _i, возникающая, в замкнутом контуре, равна скорости изменения во времени потока магнитной индукции Ф, пронизывающего контур. Это равенство принято записывать в виде

(56.3)

Знак «–» означает, что направление e _i и направление d Ф связаны правилом левого винта. (Поток Ф и его приращение d Ф – скалярные величины. Поэтому об их направлении можно говорить лишь в том смысле, какой вкладывается, например, в понятие направления тока.) Положительному приращению потока, имеющего направление за чертеж (рис. 106), соответствует изображенное на рисунке направление e _i, которое связано с направлением за чертеж правилом левого винта. Если бы проводник 1–2 перемещался не вправо, а влево, поток через контур уменьшался бы и e _i имела бы направление, противоположное изображенному на рисунке.

Единицей потока магнитной индукции в СИ служит вебер (вб), который представляет собой поток через поверхность в 1 м², пересекаемую нормальными к ней линиями магнитного поля с В, равной 1 тесла. При скорости изменения потока, равной 1 вб/сек, в контуре индуцируется э. д. с, равная 1 в.

В расссмотренном нами выше примере роль сторонних сил, поддерживающих ток в контуре, играют силы Лоренца. Работа этих сил над единичным положительным зарядом, равная по определению э. д. с., оказывается отличной от нуля. Это обстоятельство находится в кажущемся противоречии с утверждением о том, что сила Лоренца работы над зарядом совершать не может. Дело в том, что сила (56.1) представляет собой не всю лоренцеву силу, действующую на электрон, а лишь параллельную проводу составляющую силы, обусловленную скоростью v (рис. 108). Под действием этой составляющей электрон приходит

Рис. 108.

в движение вдоль провода со скоростью u, в результате чего возникает перпендикулярная к проводу составляющая лоренцевой силы f _^ модуль которой равен

f _^ = еuВ (56.7)

(см. рис. 108). Заметим, что эта составляющая не вносит вклада в циркуляцию, так как ее проекция на направление провода равна нулю.

Таким, образом, полная лоренцева сила, действующая на электрон, равна

f _Л = f _ïï + f _^

а работа этой силы над электроном за время d t

dA = f _ïï u dt – f _^ v dt

(направления векторов f _ïï и u одинаковы, а векторов f _^ и v противоположны; см. рис. 108). Учтя, что f _ïï = qvB, f _^ = еuВ, легко видеть, что работа полной силы Лоренца действительно, как и полагается, равна нулю.

Сила f _^ направлена противоположно скорости провода v. Поэтому для того, чтобы участок провода 1–2 перемещался, как показано на рис. 108, с постоянной скоростью v, к нему нужно приложить внешнюю силу f _вн, уравновешивающую сумму сил f _^, приложенных ко всем электронам, содержащимся в проводе 1–2. За счет работы этой силы и будет возникать энергия, выделяемая в контуре индуцированным током. Действительно, модуль силы f _вн можно представить в виде

f _вн = f _^ nV = euBnV = euBnlS _пр

где n – число свободных электронов в единице объема, V = lS _пp – объем провода на участке 1–2, S _пр – площадь поперечного сечения провода.

Работа силы f _вн за время d t равна

d A _вн = f _вн v d t = euBnlS _np v d t. (56.8)

Энергия, выделяемая током в контуре за время d t, определяется следующим выражением:

d Q = e _i I d t = e _i jS _прd t,

где j – плотность тока. Плотность тока равна j = еnu, согласно (56.2) э. д. с. индукции можно представить в виде e _i = vBl.

Подставив эти значения j и e _i в выражение для d Q, придем к формуле

dQ = vBlenuS _np d t,

совпадающей с формулой (56.8) для d A _вн. Таким образом, мы показали, что d Q = d A _вн.

Рассмотренное нами объяснение возникновения э. д. с. индукции относится к случаю, когда магнитное поле постоянно, а изменяется геометрия контура. Но магнитный поток через контур может изменяться также за счет изменения В. В этом случае объяснение возникновения э. д. с. оказывается в принципе другим. Изменяющееся со временем магнитное поле В порождает вихревое электрическое поле Е (подробнее об этом говорится ниже). Под действием поля Е приходят в движение носители тока в проводнике – возникает индуцированный ток. Связь между э. д. с. индукции и изменениями магнитного потока и в этом случае описывается формулой (56.3).

Пусть контур, в котором, индуцируется э. д. с, состоит не из одного витка, а из N одинаковых витков, т. е. представляет собой соленоид. Поскольку витки соленоида соединяются последовательно и согласованным образом, e _i будет равна сумме э. д. с, индуцируемых в каждом из витков в отдельности,

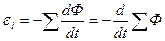
Величину

(56.9)

называют потокосцеплением или полным магнитным потоком. Ее измеряют в тех же единицах, что и Ф. Если поток, пронизывающий каждый из витков, одинаков,

y = NФ. (56.10)

Воспользовавшись потокосцеплением, выражение для э. д. с, индуцируемой в соленоиде, можно записать в виде

(56.11)

Пример. Катушка, имеющая N витков, вращается в однородном магнитном поле с постоянной скоростью w (рис. 109). Найдем индуцируемую в ней э. д. с. Поток через один виток Ф = B _n S = BS cos a, где S – площадь витка, a – угол между нормалью к плоскости витка и направлением В.

Полный поток y = NФ = NBS cos a. Угол a меняется со временем по закону a = wt. Следовательно,

y = NBS cos wt = y _mcos w t,

где через y _m обозначено амплитудное значение полного потока. По формуле (56.11)

(56.12)

Таким образом, в катушке индуцируется переменная э. д. с, изменяющаяся со временем по гармоническому закону.

Токи Фуко.

Индукционные токи могут возбуждаться и в сплошных массивных проводниках. В этом случае они называются токами Фуко или вихревыми токами.

Поскольку электрическое сопротивление массивного проводника мало, вихревые токи могут достигать очень большой силы. Токи Фуко подчиняются правилу Ленца – они выбирают внутри проводника такие пути и направления, чтобы своим действием возможно сильнее противиться причине, которой они вызваны. Поэтому движущиеся в сильном магнитном поле

Рис. 112.

хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Этим пользуются для успокоения (демпфирования) подвижных частей гальванометров, сейсмографов и других приборов. На подвижной части прибора укрепляется проводящая (например, алюминиевая) пластинка в виде сектора (рис. 112), которая вводится в зазор между полюсами сильного постоянного магнита. При движении пластинки в ней возникают вихревые токи, вызывающие торможение системы. Преимущество такого устройства состоит в том, что торможение возникает лишь при движении пластинки и отсутствует, когда пластинка неподвижна. Поэтому электромагнитный успокоитель совершенно не препятствует точному приходу системы в положение равновесия.

Тепловое действие токов Фуко используется в индукционных печах. Такая печь представляет собой катушку, питаемую высокочастотным током большой силы. Если поместить внутрь катушки проводящее тело, в нем возникнут интенсивные, вихревые токи, которые могут разогреть тело до плавления. Таким способом осуществляют плавление металлов в вакууме, что позволяет получать материалы исключительно высокой чистоты.

С помощью токов Фуко осуществляется также прогрев внутренних металлических частей вакуумных установок для их обезгаживания.

В многих случаях токи Фуко бывают нежелательными и приходится принимать для борьбы с ними специальные меры. Так, например, чтобы предотвратить потери энергии на нагревание вихревыми токами сердечников трансформаторов, эти сердечники набираются из тонких пластин, разделенных изолирующими прослойками. Пластинки располагаются так, чтобы возможные направления токов Фуко были к ним перпендикулярными. Появление ферритов (магнитных материалов с большим электрическим сопротивлением) сделало возможным изготовление сердечников сплошными.

Вихревые токи, возникающие в проводах, по которым текут переменные токи, направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате быстропеременный ток оказывается распределенным по сечению провода неравномерно – он как бы вытесняется на поверхность проводника. Это явление называется скин-эффектом (от английского skin – кожа) или поверхностным эффектом. Из-за скин-эффекта внутренняя часть проводников в высокочастотных цепях оказывается бесполезной. Поэтому в высокочастотных цепях применяют проводники в виде трубок.

Явление самоиндукции.

Электрический ток i, текущий в любом контуре, создает пронизывающий этот контур магнитный поток y. При изменениях i будет изменяться также y и, следовательно, в контуре будет индуцироваться э. д. с. Это явление называется самоиндукцией.

В соответствии с законом Био – Савара магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток в контуре i и создаваемый им полный магнитный поток через контур y друг другу пропорциональны:

y = Li. (59.1)

Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура.

Линейная зависимость y от i имеет место лишь в том случае, если относительная магнитная проницаемость m среды, которой окружен контур, не зависит от напряженности поля Н, т. е. в отсутствие ферромагнетиков. В противном случае m является сложной функцией от i (через Н), и, поскольку В = m ₀ mН, зависимость y от i также будет довольно сложной. Однако соотношение (59.1) распространяют и на этот случай, считая индуктивность L функцией от i. При неизменной силе тока i полный поток y может изменяться за счет изменений формы и размеров контура.

Из сказанного следует, что индуктивность L зависит от геометрии контура (т. е. его формы и размеров) и от магнитных свойств (от m,) окружающей контур среды.

Если контур жесткий и поблизости от него нет ферромагнетиков, индуктивность L будет постоянной величиной.

За единицу индуктивности в СИ принимается индуктивность такого проводника, у которого при силе тока в нем в 1 а возникает полный поток y, равный 1 вб. Эту единицу называют генри (гн).

Вычислим индуктивность соленоида. Возьмем соленоид такой длины, чтобы его можно было практически считать бесконечным. При протекании по нему тока i внутри соленоида возбуждается однородное поле, магнитная индукция которого согласно формулам (42.6) и (44.24) равна В = m ₀ mni. Поток через каждый из витков будет Ф = BS, а полный магнитный поток, сцепленный с соленоидом, равен

y = NФ = nlBS = m ₀ mn ² lSi (59.4)

где l – длина соленоида (которая предполагается очень большой), S – площадь поперечного сечения, n – число витков на единицу длины (произведение nl дает полное, число витков N).

Сопоставляя (59.4) с (59.1), получаем для индуктивности очень длинного соленоида следующее выражение:

L = m ₀ mn ² lS = m ₀ mn ² V (59.5)

где V = lS – объем соленоида. Заменив в (59.5) n через N / l, получим

L = m ₀ mN ² S / l (59.6)

В соответствии с (59.6) размерность m ₀ равна размерности индуктивности, деленной на размерность длины (напомним, что относительная магнитная проницаемость m – безразмерная величина). Следовательно, в СИ m ₀ измеряется в генри на метр.

При изменениях силы тока в контуре возникает э. д. с. самоиндукции e _S, равная

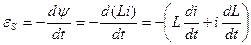(59.8)

Если L при изменениях силы тока остается постоянной (что, как уже отмечалось, возможно лишь при отсутствии ферромагнетиков), выражение для e _S имеет вид

e _S = – L d i /d t (59.9)

Соотношение (59.9) дает возможность определить индуктивность L как коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого э. д. с. самоиндукции. Однако такое определение правильно лишь в случае, когда L = const. В присутствии ферромагнетиков L недеформируемого контура будет функцией от i (через Н); следовательно, d L /d t можно записать как (d L /d i)(d i /d t). Произведя такую подстановку в формуле (59.8), получим

(59.11)

откуда видно, что при наличии ферромагнетиков коэффициент пропорциональности между d i /d t и e _S отнюдь не равен L.

В случае, когда L = const, изменение силы тока со скоростью 1 а/сек в проводнике с L = 1 Гн приводит согласно (59.9) к возникновению e _S = 1в.

Энергия магнитного поля.

Рассмотрим цепь, изображенную на рис. 115. Сначала замкнем соленоид L на батарею e в нем установится ток i; который обусловит магнитное поле, сцепленное с витками соленоида.

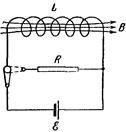Рис.115

Если, отключив соленоид от батареи, замкнуть его через сопротивление R, то в образовавшейся цепи будет некоторое время течь постепенно убывающий ток. Работа, совершаемая этим током за время d t, равна

d A = e _S i d t = – (d y /d t) i d t = – i d y. (61.1)

Если индуктивность соленоида не зависит от t (L = const), то d y = L d i и выражение (61.1) принимает следующий вид:

d A =°– Li d i. (61.2)

Проинтегрировав это выражение по i в пределах от первоначального значения i до нуля, получим работу, совершаемую в цепи за все время, в течение которого происходит исчезновение магнитного поля:

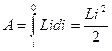(61.3)

Работа (61.3) идет на приращение внутренней энергии проводников, т. е. на их нагревание. Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве.1 Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа (61.3). Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток i, обладает энергией

W = Li ²/2 (61.4)

которая локализована в возбуждаемом током магнитном поле [ср. эту формулу с выражением для энергии заряженного конденсатора].

Заметим, что выражение (61.3) можно трактовать как ту работу, которую необходимо совершить против э. д. с. самоиндукции в процессе нарастания тока от 0 до i, и которая идет на создание магнитного поля, обладающего энергией (61.4). В самом деле, работа, совершаемая против э. д. с. самоиндукции,

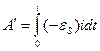
Произведя преобразования, подобные тем, которые привели нас к выражению (61.2), получим

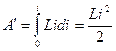(61.6)

что совпадает с (61.3). Работа (61.6) совершается при установлении тока за счет источника э. д. с. и идет целиком на создание сцепленного с контуром магнитного поля. Выражение (61.6) не учитывает той работы, которую источник э. д. с. затрачивает в процессе установления тока на нагревание проводников. Она равна

.

Выразим энергию магнитного поля (61.4) через величины, характеризующие само поле. В случае бесконечного (практически очень длинного) соленоида

L = m ₀ mn ² V, Н = ni,

откуда

i = H / n

Подставляя эти значения L и i в (61.4) и производя преобразования, получим

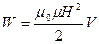(61.7)

Было показано, что магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия (61.7) заключена в пределах соленоида и распределена по его объему с постоянной плотностью w, которую можно получить, разделив W на V. Произведя это деление, получим

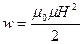(61.8)

Воспользовавшись соотношением (44.15), формулу для плотности энергии магнитного поля можно записать следующим образом:

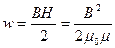(61.9)

Полученное нами выражение для плотности энергии магнитного поля имеет вид, аналогичный выражению (30.2) для плотности энергии электрического поля, с тем лишь отличием, что электрические величины в нем заменены соответствующими магнитными.

Если магнитное поле неоднородно, плотность энергии больше там, где больше Н и m. Чтобы найти энергию магнитного поля, заключенную в некотором объеме V, нужно вычислить интеграл

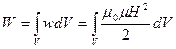(61.11)

Электромагнитное поле. Вихоевое электрическое поле.

Рассмотрим случай электромагнитной индукции, когда контур, в котором индуцируется ток, неподвижен, а изменения потока магнитной индукции обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменения магнитного поля вызывают появление в контуре сторонних сил, действующих на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в контуре; они также не могут быть силами Лоренца, так как силы Лоренца работы над зарядом не совершают. Остается заключить, что индукционный ток обусловлен возникающим в контуре электрическим полем.

Обозначим напряженность этого поля Е _В. Согласно формуле (32.2) э. д. с. индукции равна циркуляции вектора Е _В по контуру:

(103.1)

В соответствии с формулой (56.3),

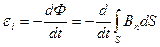(103.2)

где интеграл берется по произвольной поверхности, опирающейся на контур. Поскольку контур неподвижен, операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:

(103.3)

Вектор В зависит как от времени, так и от координат. В правой части уравнения (103.3) имеется в виду производная по времени от В в соответствующей неизменной точке поверхности. Поэтому в подынтегральном выражении применен символ частной производной по времени.

Произведя замену (103.3) в формуле (103.2) и приравняв затем выражения (103.1) и (103.2) для e _i, получим

(103.4)

Максвелл предположил, что изменяющееся со временем магнитное поле обусловливает появление, в пространстве поля Е _В, независимо от присутствия в этом пространстве проводящего контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.

Итак, согласно идее Максвелла изменяющееся со временем магнитное поле порождает электрическое поле. Это поле Е _В существенно отличается от порождаемого неподвижными зарядами электростатического поля Е.

Электростатическое поле потенциально, его линии напряженности начинаются и заканчиваются на зарядах. Циркуляция вектора Е _q по любому контуру равна нулю [см. формулу (9.2)]

(103.5)

Согласно формуле (103.4) циркуляция вектора Е _В отлична от нуля. Следовательно, поле Е _В, как и магнитное поле, оказывается вихревым. Линии напряженности поля Е _В замкнуты.

Таким образом, электрическое поле может быть как потенциальным (Е _q), так и вихревым (Е _в). В общем случае электрическое поле может слагаться из поля Е _q, создаваемого зарядами, и поля Е _В, обусловленного изменяющимся со временем магнитным полем. Сложив вместе выражения (103.5) и (103.4), получим для напряженности суммарного поля Е = Е _q + Е _в следующее соотношение:

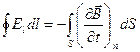(103.6)

Интеграл в левой части берется по произвольному замкнутому контуру, в правой части – по произвольной поверхности, опирающейся на этот контур.

Выражение (103.6) является одним из основных уравнений электромагнитной теории Максвелла.

Ток смещения.

Как было выяснено, из явления электромагнитной индукции вытекает, что наличие в пространстве изменяющегося магнитного поля приводит к возникновению вихревого электрического поля. Основная идея Максвелла заключается в том, что между электрическим и магнитным полями имеется и обратное соотношение, т. е. что изменяющееся со временем электрическое поле должно приводить к появлению магнитного поля. Эта идея оказалась исключительно плодотворной.

Разработанная Максвеллом на ее основе электромагнитная теория получила блестящее экспериментальное подтверждение.

Для установления количественных соотношений между изменяющимся электрическим и возникающим магнитным полями Максвелл ввел в рассмотрение так называемый ток смещения.

Рассмотрим цепь квазистационарного переменного тока, содержащую конденсатор (рис. 228). Движение свободных носителей заряда, т. е. ток проводимости, имеет место во всей цепи, кроме зазора между обкладками конденсатора. Следовательно, линии тока проводимости терпят на границах обкладок разрыв. Зато в пространстве между обкладками имеется переменное электрическое поле, которое можно охарактеризовать смещением D. Максвелл предположил, что линии тока проводимости непрерывно переходят на границе обкладок в линии тока, названного им током смещения.

Мгновенное значение силы тока равно i = d q /d t. Плотность тока проводимости в непосредственной близости от поверхности обкладок определяется выражением

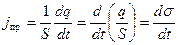
Рис. 228.

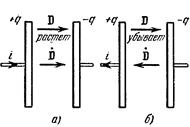Рис. 229.

где S – площадь обкладки, q – распределенный на ней заряд, s – поверхностная плотность заряда.

Чтобы линии тока смещения имели такую же густоту, как и линии тока проводимости, плотность тока смещения j _см также должна быть равна d s /d t. Выразим j _см через параметры электрического поля, имеющегося в зазоре. Согласно формулам (16.19) и (8.6) электрическое смещение в зазоре между обкладками равно D = e₀ E ₀ = s, откуда d s /d t = d D /d t.

Таким образом, нужно положить

j _см = d D /d t (105.1)

Рис. 229 поясняет, что направление вектора j _np, a следовательно и вектора j _см, совпадает с направлением вектора . При указанных на рис. 229а знаках зарядов и направлении тока j вектор j _np направлен слева направо. Вектор D также направлен слева направо и растет по величине. Следовательно, приращение вектора D, а значит и вектор , имеет то же направление, что и j _np.

Дата добавления: 2015-04-24