Взаимодействие токов. 6 страница

При направлении тока, указанном на рис. 229 б, вектор D убывает по величине. Следовательно, вектор направлен справа налево, т. е. опять так же, как и вектор j _np. На этом основании выражение (105.1) можно написать в векторном виде

j _см = d D /d t. (105.2)

Формулу (105.2), определяющую плотность тока смещения, Максвелл распространил на электрические поля любого вида, в том числе и на вихревые поля. Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Согласно Максвеллу при расчетах магнитных полей в формулы нужно подставлять полную плотность тока, слагающуюся из плотности тока проводимости и плотности тока смещения:

j _полн = j _np + j _см = j _np + d D /d t (105.3)

В частности, циркуляция вектора Н по любому контуру должна быть равна

(105.4)

Уравнение (105.4) представляет собой второе основное уравнение теории Максвелла.

Согласно формуле (105.2) ток смещения имеется везде, где есть изменяющееся электрическое поле. Следовательно, он существует и внутри проводника, по которому течет переменный электрический ток. Однако внутри проводов j _см обычно бывает пренебрежимо мал по сравнению с j _пр.

Электромагнитное поле. Уравнения Максвелла в интегральной форме.

Согласно идеям Максвелла переменное магнитное поле всегда связано с порождаемым им электрическим полем, в свою очередь переменное электрическое поле всегда связано с порождаемым им магнитным. Таким образом, электрическое и магнитное поля оказываются неразрывно связанными друг с другом – они образуют единое электромагнитное поле.

Проведенное выше рассмотрение электрических и магнитных явлений показало отличное согласие экспериментальных соотношений с выводами, полученными на основе динамических (механических) моделей процессов. Поэтому принцип относительности, установленный Галилеем для механических явлений, должен быть распространен и на все другие физические явления. Согласно принципу относительности, сформулированному Эйнштейном с учетом результатов неизвестных во времена Галилея, законы всех физических явлений, в том числе и электромагнитных, имеют одинаковый вид (т. е. описываются одинаковыми уравнениями) во всех инерциальных системах отсчета.

Из принципа относительности вытекает, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, электростатическое поле создается системой неподвижных зарядов. Однако, если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти заряды движутся и, следовательно, будут порождать не только электрическое, но и магнитное поле (движущийся заряд эквивалентен току). Неподвижный провод с постоянным током создает в каждой точке пространства постоянное магнитное поле. Однако относительно других инерциальных систем этот провод находится в движении. Поэтому создаваемое им магнитное поле в любой точке с данными координатами х, у, z будет меняться и, следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается «чисто» электрическим или «чисто» магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей.

Теория Дурде. Закон Ома. Закон Джоуля-Ленца.

Исходя из представлений о свободных электронах, Друде разработал классическую теорию металлов, которая затем была усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно, пробегая в среднем некоторый путь. Правда, в отличие от молекул газа, пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле

(70.1)

Для комнатной температуры (~300°К) вычисление по этой формуле приводит к следующему значению:

При включении поля на хаотическое тепловое движение, происходящее со скоростью (70.1), накладывается упорядоченное движение электронов с некоторой средней скоростью u. Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью u:

j = neu (70.2)

Предельная допустимая техническими нормами плотность тока для медных проводов составляет около 10 а/мм² = 10⁷ а/м². Взяв для n значение 10²³ см^–3 = 10²⁹ м^–3, получим

Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения зарядов (u) в 10⁸ раз меньше средней скорости теплового движения (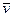). Поэтому при вычислениях модуль результирующей скорости | v + u | всегда можно заменить модулем скорости теплового движения | v |.

Найдем вызванное полем изменение среднего значения кинетической энергии электронов. Средний квадрат результирующей скорости равен

. Последнее равенство справедливо, так как среднее значение v равно нулю (хаотичное движение).

Следовательно, упорядоченное движение увеличивает кинетическую энергию электронов в среднем на

(70.3)

Закон Ома.

Эксперимент.

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:

Однородным называется проводник, в котором не действуют сторонние силы. В этом случае напряжение U совпадает с разностью потенциалов, поддерживаемой на концах проводника. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит ом, равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой в 1 а.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

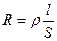
где l – длина проводника, S – площадь его поперечного сечения, r – зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если l = 1 и S = 1, то R численно равно r. В СИ r измеряется в ом метрах (ом×м).

Закон Ома можно записать в дифференциальной форме. Выделим мысленно в окрестности

Рис.

некоторой точки внутри проводника элементарный цилиндрический объем (рис.) с образующими, параллельными вектору плотности тока j в данной точке. Через поперечное сечение цилиндра течет ток силой j d S. Напряжение, приложен–ное к цилиндру, равно E d l где Е – напряженность поля в данном месте. Наконец, сопротивление цилиндра равно r ×d l /d S. Тогда закон Ома примет вид:

Носители заряда в каждой точке движутся в направлении вектора Е. Поэтому направления j и Е совпадают. Таким образом, можно написать

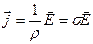
где s = 1/ r – величина, называемая коэффициентом электропроводности или просто проводимостью материала.

Полученная формула выражает закон Ома в дифференциальной форме.

Способность вещества проводить ток характеризуется его удельным сопротивлением r либо проводимостью s. Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:

r = r ₀ (1 + a t °)

где r ₀ – удельное сопротивление при 0°С, t ° – температура по шкале Цельсия, a – размерный коэффициент характерный для данного материала.

При низких температурах наблюдаются отступления от этой закономерности (рис.). В большинстве случаев зависимость r от Т следует кривой 1. Величина остаточного

Рис.

сопротивления r _ост в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце.

Поэтому после отжига r _ост заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле r = 0.

У большой группы металлов и сплавов при температуре порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (на рис. кривая 2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг–Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена, у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Т _к, при которой он переходит в сверхпроводящее состояние.

При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля Н _к, разрушающего сверхпроводимость, равна нулю при Т = Т _к и растет с понижением температуры.

Теория. Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение, равное eE / m, и к концу пробега скорость упорядоченного движения достигнет в среднем значения

u _mах = (eE / m) t (70.4)

где t – среднее время между двумя последовательными соударениями электрона с ионами решетки.

Друде не учитывал распределения электронов по скоростям и приписывал всем электронам одинаковое значение скорости v. В этом приближении t = l / v где l – среднее значение длины свободного пробега, v – скорость теплового движения электронов (мы воспользовались тем, что | v + u | практически равен | v |).

Подставим это значение t в формулу (70.4):

u _mах = eEl / mv (70.5)

Скорость u изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального:

Подставив это выражение в формулу (70.2), получим

Плотность тока оказалась пропорциональной напряженности поля. Если учесть, что плотность тока, величина тока, разность потенциалов и напряженность поля связаны соотношениями пропорциональности, можно утверждать, что мы получили закон Ома. Коэффициент пропорциональности между j и Е представляет собой проводимость

(70.6)

Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами, расположенными в узлах кристаллической решетки металла.

Закон Джоуля – Ленца.

Эксперимент.

При прохождении по проводнику тока проводник нагревается. Джоуль и независимо от него Ленц обнаружили экспериментально, что количество выделяющегося в проводнике тепла пропорционально его сопротивлению, квадрату силы тока и времени:

Q = Ri ² t.

Легко сообразить, что если сила тока изменяется со временем, то

Оба приведенных соотношения выражают закон Джоуля – Ленца. Подставляя R в омах, i в амперах, a t в секундах, Q получим в джоулях.

Закон имеет следующее объяснение. Рассмотрим однородный проводник, к которому приложено напряжение U. За время d t через каждое сечение проводника проходит заряд d q = i dt. Это равносильно тому, что заряд d q = i d t переносится за время d t из одного конца проводника в другой. При этом силы поля совершают работу d A = U d q = Ui d t. Заменяя U в соответствии с законом Ома через Ri и интегрируя, получим для работы электрических сил выражение, совпадающее с выражением для Q. Таким образом, нагревание проводника происходит за счет работы, совершаемой силами поля над носителями заряда.

От формулы, определяющей тепло, выделяемое во всем проводнике, можно перейти к выражению, характеризующему выделение тепла в различных местах проводника. Выделим в проводнике таким же образом, как это было сделано при выводе формулы закона Ома, элементарный объем в виде цилиндра. Согласно закону Джоуля – Ленца за время d t в этом объеме выделится тепло

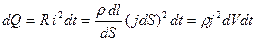
где d V = d S d l – величина элементарного объема. Количество тепла d Q, отнесенное к единице времени и единице объема, назовем удельной мощностью тока w. Получаем

w = rj ²

Воспользовавшись соотношением между j, E, r и s, формуле можно придать следующий вид:

w = jE = sE ²

Полученная формула выражает закон Джоуля – Ленца в дифференциальной форме.

Теория. К концу свободного пробега электрон приобретает дополнительную кинетическую энергию, средняя величина которой согласно формулам (70.3) и (70.5) равна

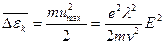(70.7)

Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, т. е. передает энергию (70.7) кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании.

Каждый электрон претерпевает за секунду в среднем 1/ t = v / l соударений, сообщая всякий раз решетке энергию (70.7). Следовательно, в единице объема за единицу времени, должно выделяться тепло

где n – число электронов проводимости в единице объема. Величина w есть не что иное, как удельная мощность тока. Множитель при Е ² совпадает со значением (70.6) для s. Таким образом, мы пришли к выражению (34.5) закона Джоуля – Ленца.

Закон Видемана – Франца.

Эксперимент. Из опыта известно, что наряду с высокой электропроводностью металлы отличаются также большой теплопроводностью. Видеман и Франц установили в 1853 г. эмпирический закон, согласно которому отношение коэффициента теплопроводности и к коэффициенту электропроводности s для всех металлов приблизительно одинаково и изменяется пропорционально абсолютной температуре. Так, например, при комнатной температуре это отношение равно для алюминия 5.8 10^-6, для меди 6.4 10^-6 и для свинца 7.0 10^–6 дж ом/сек град.

Теория. Способностью проводить тепло обладают и неметаллические кристаллы. Однако теплопроводность металлов значительно превосходит теплопроводность диэлектриков. Из этого можно заключить, что теплопередача в металлах осуществляется в. основном не кристаллической решеткой, а электронами. Рассматривая электроны как одноатомный газ, для коэффициента теплопроводности можно использовать выражение для теплопроводности, полученное в кинетической теории газов

(nm – плотность газа, v – тепловая скорость частиц газа).

Удельная теплоемкость одноатомного газа равна

.

Подставляя это значение в выражение для k, получим

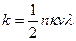
Разделим k на выражение (70.6) для s

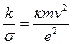
Произведя замену , приходим к соотношению

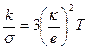
которое выражает закон Видемана – Франца.

Подставив к = 1.38 10^-23 дж/град и е = 1.6 10^-19 К, получим .

При Т = 300° К для отношения k / s получается значение6.7 10^–6 дж ом/сек град, очень хорошо согласующееся с экспериментальными данными (см. приведенные выше значения для Аl, Сu и Рb). Однако, как выяснилось впоследствии, столь хорошее совпадение оказалось случайным, ибо когда Лоренц уточнил расчеты, учтя распределение электронов по скоростям, для отношения k / s получилось значение , которое хуже согласуется с данными опыта.

Итак, классическая теория, смогла объяснить законы Ома и Джоуля – Ленца, а также дала качественное объяснение закона Видемана – Франца. Вместе с тем эта теория встретилась с весьма существенными затруднениями. Из них основными являются два. Из формулы (70.6) вытекает, что сопротивление металлов (т. е. величина, обратная s) должно возрастать как корень квадратный из Т. В самом деле, для предположений о зависимости от температуры величин n и l нет никаких оснований. Скорость же теплового движения пропорциональна корню из Т. Этот вывод теории противоречит опытным данным, согласно которым электрическое сопротивление металлов растет пропорционально первой степени Т, т. е. быстрее, чем .

Второе затруднение классической теории заключается в том, что электронный газ должен обладать молярной теплоемкостью, равной . Добавляя эту величину к теплоемкости решетки, составляющей 3 R, мы получим для килограмм–атомной теплоемкости металла значение . Таким образом, согласно классической электронной теории килограмм–атомная теплоемкость металлов должна быть в 1,5 раза больше, чем у диэлектриков. В действительности же теплоемкость металлов не отличается заметно от теплоемкости неметаллических кристаллов. Объяснение такого несоответствия смогла дать лишь квантовая теория металлов.

Несмотря на неспособность классической теории дать объяснение ряда явлений, она сохранила значение и до настоящего времени, потому что в случае малых концентраций свободных электронов (что имеет место в полупроводниках) она дает вполне удовлетворительные результаты. Вместе с тем по сравнению с квантовой теорией классическая обладает значительной простотой и наглядностью.

Основы квантовой теории твердых тел.

В классической теории металлов считалось само собой разумеющимся, что электроны проводимости могут обладать любыми значениями энергии. Согласно квантовой теории энергия электронов в любом кристаллическом теле (в частности, в металле) так же, как и энергия электронов в атоме, квантуется. Это означает, что она может принимать лишь дискретные (т. е. разделенные конечными промежутками) значения, называемые уровнями энергии. Дозволенные уровни энергии в кристалле группируются в зоны.

Чтобы понять происхождение зон, рассмотрим воображаемый процесс объединения атомов в кристалл.

Рис. 135

Пусть первоначально имеется N изолированных атомов какого–либо вещества. Каждый электрон любого атома обладает одним из разрешенных значений энергии, т. е. занимает один из дозволенных энергетических уровней. В основном, невозбужденном состоянии атома суммарная энергия электронов имеет минимальное возможное значение. Поэтому, казалось бы, все электроны должны находиться на самом низком уровне. Однако электроны подчиняются принципу запрета Паули, который гласит, что в любой квантовой системе (атоме, молекуле, кристалле и т. д.) на каждом энергетическом уровне1) может находиться не более двух электронов, причем собственные моменты (спины) электронов, занимающих одновременно один и тот же уровень,, должны иметь противоположные направления2). Следовательно, на самом низком уровне атома может разместиться только два электрона, остальные заполняют попарно более высокие уровни. На рис. 135 показано размещение электронов по уровням в основном состоянии атома, имеющего 5 электронов.

Схема уровней изображена условно, без соблюдения масштаба. Электроны обозначены кружками со стрелкой. Разные направления стрелок соответствуют противоположным направлениям спинов.

Пока атомы изолированы друг от друга они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах. По мере сближения атомов между ними возникает все усиливающееся взаимодействие, которое приводит к изменению положения уровней. Вместо одного одинакового для всех N атомов уровня возникают N очень близких, но не совпадающих уровней.

Таким образом, каждый уровень – изолированного атома расщепляется в кристалле на N густо расположенных уровней, образующих полосу или зону. Величина расщепления для разных уровней не одинакова. Уровни, заполненные в атоме более близкими к ядру (внутренними) электронами, возмущаются меньше, чем уровни, заполненные внешними электронами.

Принципу Паули подчиняются не только электроны, но и все другие частицы с полуцелым спином]. На рис. 136 показано расщепление различных уровней как функция расстояния г– между атомами. Отмеченные на рисунке значения r ₁ и r ₂ соответствуют расстояниям между атомами в двух различных кристаллах. Из схемы видно, что возникающее в кристалле расщепление уровней, занятых внутренними электронами, очень мало. Заметно расщепляются лишь уровни, занимаемые валентными электронами. Такому же расщеплению подвергаются и более высокие уровни, не занятые электронами в основном состоянии атома.

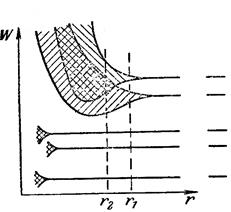Рис 136

При достаточно малых расстояниях между атомами может произойти перекрывание зон, соответствующих двум соседним уровням атома (см. пунктирную прямую, отвечающую расстоянию r ₂ между атомами). Число уровней в такой слившейся зоне равно сумме количеств уровней, на которые расщепляются оба уровня атома.

Взаимодействующие атомы представляют собой единую квантовую систему, в пределах которой действует принцип запрета Паули. Следовательно, 2N электронов, которые заполняли какой–то уровень в изолированных атомах, разместятся в кристалле попарно (с противоположными спинами) на N уровнях соответствующей полосы.

Нижние, образованные слабо расщепленными уровнями зоны заполняются электронами, каждый из которых не утрачивает и в кристалле прочной связи со своим атомом. Эти зоны и заполняющие их электроны в дальнейшем интересовать нас не будут. Дозволенные значения энергии валентных электронов в кристалле объединяются в зоны, разделенные промежутками, в которых разрешенных значений энергии нет. Эти промежутки называются запрещенными зонам и. Ширина разрешенных и запрещенных зон не зависит от размеров кристалла. Таким образом, чем больше атомов содержит кристалл, тем теснее располагаются уровни в зоне. Ширина разрешенных зон имеет величину порядка нескольких электронвольт. Следовательно, если кристалл содержит 10²³ атомов, расстояние между соседними уровнями в зоне составляет ~ 10^–23 эв.

Рис. 137.

При абсолютном нуле энергия кристалла должна быть минимальной. Поэтому валентные электроны заполнят попарно нижние уровни разрешенной зоны, возникшей из того уровня, на котором находятся валентные электроны в основном состоянии атома (мы будем называть ее валентной зоной). Более высокие разрешенные зоны будут от электронов свободны. В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны возможны три случая, изображенные на рис. 137. В случае а) электроны заполняют валентную зону не полностью. Поэтому достаточно сообщить электронам, находящимся на верхних уровнях, совсем небольшую энергию (<~10^–23 – 10^–22 эв) для того, чтобы перевести их на более высокие уровни. Энергия теплового движения (kT) составляет при 1 К величину порядка 10^–4 эв (при комнатной температуре – 1/40 эв).

Следовательно, при температурах, отличных от 0°К, часть электронов переводится на более высокие уровни.

Дополнительная энергия, вызванная действием на электрон электрического поля, также оказывается достаточной для перевода электрона на более высокие уровни. Поэтому электроны могут ускоряться электрическим полем и приобретать дополнительную скорость в направлении, противоположном направлению поля. Таким образом, кристалл с подобной схемой энергетических уровней будет представлять собою металл.

Частичное заполнение валентной зоны (в случае металла ее называют также зоной проводимости) может произойти, если на последнем занятом уровне в атоме находится только один электрон; или имеет место перекрывание зон (см. рис. 136, расстояние r ₂). В первом случае N электронов проводимости заполняют попарно только половину уровней валентной зоны. Во втором случае число уровней в зоне проводимости будет больше N, так что, даже если количество электронов проводимости равно 2 N, они не смогут занять все уровни зоны.

В случаях б) и в) уровни валентной зоны полностью заняты электронами – зона заполнена. Для того чтобы увеличить энергию электрона, необходимо сообщить ему количество энергии, не меньшее, чем ширина запрещенной зоны D W. Электрическое поле (во всяком случае, такой напряженности, при которой не происходит электрический пробой кристалла) сообщить электрону такую энергию не в состоянии. При этих условиях электрические свойства кристалла определяются шириной запрещенной зоны D W. Если D W невелико (порядка нескольких десятых электронвольта), энергия теплового движения оказывается достаточной для того, чтобы перевести часть электронов в верхнюю свободную зону. Эти электроны будут находиться в условиях, аналогичных тем, в которых находятся валентные электроны в металле. Свободная зона окажется для них зоной проводимости.

Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется электронным полупроводником.

.Если ширина запрещенной зоны D W велика (порядка нескольких– электронвольт), тепловое движение не сможет забросить в свободную зону заметное число электронов. В этом случае кристалл оказывается изолятором.

Дата добавления: 2015-04-24